
全程设计 章末核心素养整合
章末核心素养整合

知识体系构建 专题归纳突破
知识体系构建 专题归纳突破
导 知识体系构建 铁是代表性变价元素,对铁及其化合物的转化关系可以从物 质类别和元素价态的视角认识(元素价类二维图)。 化合价 +6 FeO +3 Fe,0,2 e(O田3之Fe+→FeCl,(宏观物质) ①◆ 价态变化 电子转移 +2 FeO Fe(OH2之Fe2+→FeC2(宏观物质) (微观解释) Fe 0 单质 氧化物 氢氧化物 盐物质类别
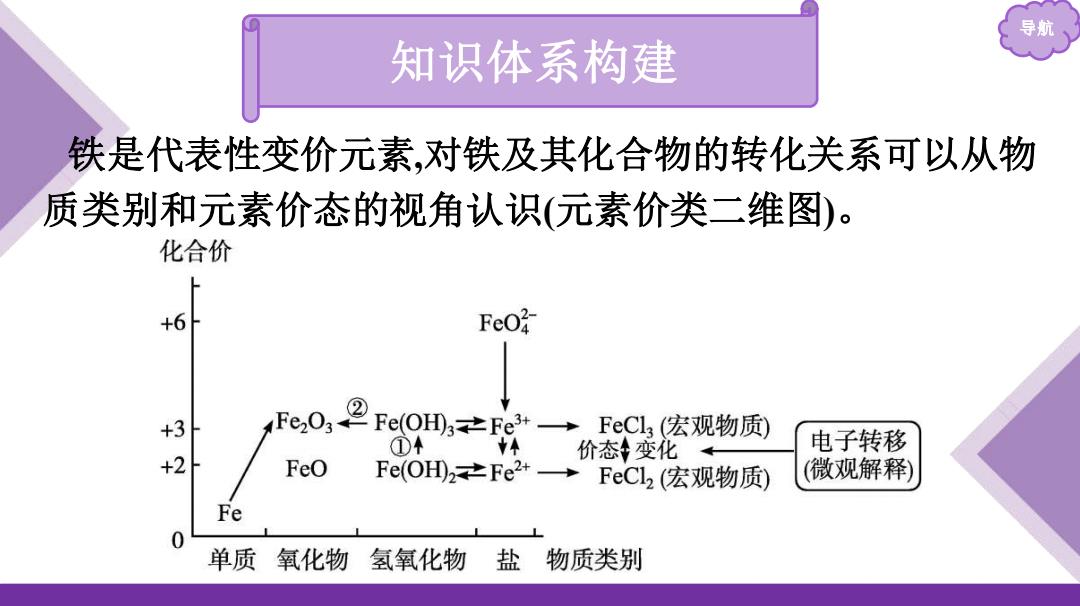
导航 知识体系构建 铁是代表性变价元素,对铁及其化合物的转化关系可以从物 质类别和元素价态的视角认识(元素价类二维图)

借助价类二维图分析典型性质举例: 1)铁元素的价类二维图中转化①的化学方程 式:4Fe(OHD2+02+2H,0一4P(OH3,溶液中发生该转化过 程的现象是白色絮状沉淀迅速变成灰绿色,最后变为红褐色 沉淀。 (2)Fe(OHD3受热易分解,转化②的化学方程式:2Fe(OHD3△ Fez03+3H20。 (3)将Fe2+转化为Fe3+需要加入氧化剂,将Fe3+转化为Fe2+需 要加入还原剂
导航 借助价类二维图分析典型性质举例: (1)铁元素的价类二维图中转化①的化学方程 式:4Fe(OH)2+O2+2H2O══4Fe(OH)3 ,溶液中发生该转化过 程的现象是白色絮状沉淀迅速变成灰绿色,最后变为红褐色 沉淀。 (2)Fe(OH)3受热易分解,转化②的化学方程式:2Fe(OH)3 Fe2O3+3H2O。 (3)将Fe2+转化为Fe3+需要加入氧化剂,将Fe3+转化为Fe2+需 要加入还原剂

导航 专题归纳突破 专题化学计算中的常用方法 1关系式法。 当已知物和未知物之间是靠多个反应来联系时,只需直接确 定已知量和未知量之间的比例关系,即“关系式
导航 专题归纳突破 专题 化学计算中的常用方法 1.关系式法。 当已知物和未知物之间是靠多个反应来联系时,只需直接确 定已知量和未知量之间的比例关系,即“关系式”

(1)根据化学方程式确定关系式:写出发生反应的化学方程 式,根据量的关系写出关系式。 如把CO还原Fe203生成的CO,通入澄清石灰水中,求生成沉 淀的量。发生反应的化学方程式: 高温 3CO+Fe2O3 Fe+3C02, C02+Ca(0HD2-CaC03↓+H20。 则关系式为3C0-3C023CaC03,即C0CaC03 (2)根据原子守恒确定关系式:上述例子中也可直接根据碳 原子守恒得出C0~CaC03
导航 (1)根据化学方程式确定关系式:写出发生反应的化学方程 式,根据量的关系写出关系式。 如把CO还原Fe2O3生成的CO2通入澄清石灰水中,求生成沉 淀的量。发生反应的化学方程式: 3CO+Fe2O3 2Fe+3CO2, CO2+Ca(OH)2 ══CaCO3↓+H2O。 则关系式为3CO~3CO2~3CaCO3 ,即CO~CaCO3。 (2)根据原子守恒确定关系式:上述例子中也可直接根据碳 原子守恒得出CO~CaCO3
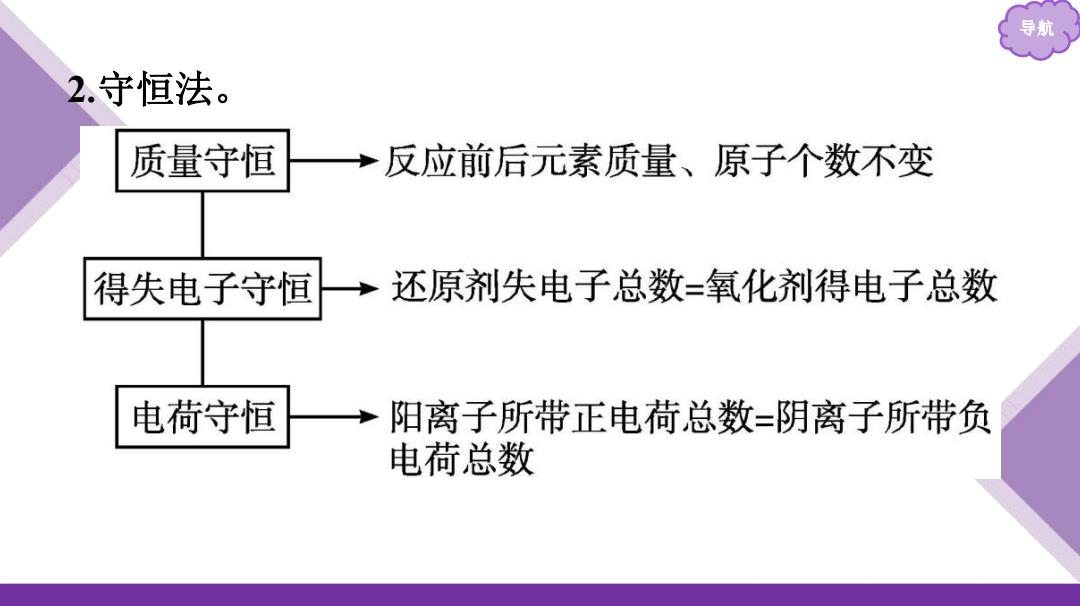
导航 2.守恒法。 质量守恒 ·反应前后元素质量、原子个数不变 得失电子守恒 ·还原剂失电子总数=氧化剂得电子总数 电荷守恒 阳离子所带正电荷总数=阴离子所带负 电荷总数
导航 2.守恒法

导 3.差量法。 根据化学反应前后物质的有关物理量发生的变化,找出“理 论差量”,如反应前后的质量差、物质的量差、气体体积差等。 该差量的大小与反应物的有关量成正比。差量法就是借助这 种比例关系,解决一定量变的计算题的方法。 例如,把一铁棒插入CuSO4溶液后,过一段时间取出,铁棒质 量增加了4g,据此可求出参加反应的Fe的质量
导航 3.差量法。 根据化学反应前后物质的有关物理量发生的变化,找出“理 论差量”,如反应前后的质量差、物质的量差、气体体积差等。 该差量的大小与反应物的有关量成正比。差量法就是借助这 种比例关系,解决一定量变的计算题的方法。 例如,把一铁棒插入CuSO4溶液后,过一段时间取出,铁棒质 量增加了4 g,据此可求出参加反应的Fe的质量

导航、 Fe+CuSO4一FeSO4+Cu△m(增加) 56g 64g8g m(Fe) 4g 56g = 8g m(Fe) 4g m(Fe)=28 g
导航 Fe+CuSO4 ══FeSO4+Cu Δm(增加) 56 g 64 g 8 g m(Fe) 4 g 𝟓𝟔 𝐠 𝒎(𝐅𝐞) = 𝟖 𝐠 𝟒 𝐠 m(Fe)=28 g

导航 4.极值法一极端假设的计算方法。 极值法就是将复杂的问题假设为处于某一个或某两个极端 状态,并站在极端的角度分析问题,求出一个极值,推出未知量 的值,或求出两个极值,确定未知量的范围,从而使复杂的问题 简单化。可用于判断混合物的组成
导航 4.极值法——极端假设的计算方法。 极值法就是将复杂的问题假设为处于某一个或某两个极端 状态,并站在极端的角度分析问题,求出一个极值,推出未知量 的值,或求出两个极值,确定未知量的范围,从而使复杂的问题 简单化。可用于判断混合物的组成