
试卷代号:2320 座位号■ 中央广播电视大学2006一2007学年度第二学期“开放专科”期末考试 物流管理专业 物流管理定量分析基础 试题 2007年7月 题 号 二 三 四 总 分 分 数 得 分 评卷人 一、单项选择题(每小题4分,共20分) 1.若某物资的总供应量大于总需求量,则可增设一个( ),其需求量取总供应量与总 需求量的差额,并取各产地到该销地的单位运价为0,可将不平衡运输问题化为平衡运输问 题。 A.虚产地 B.虚销地 C.需求量 D.供应量 minS=-x1+3x2+4x3 x1十2.x2+x3≤4 2x1十3x2+x3≥5 2.线性规划问题 的标准形式为( ) x23 x1x2x3≥0 maxS'=x1-3.x2-4.x3十0x4+0x6+0.x6 x1+2x2十xg十x4=4 2x1+3.x2十x3-x6=5 A. Ta-T6=3 x1T2,T3x45,x6≥0 1630
试卷代号 :2320 座位号巨二{ 中央广播电视大学2006-2007学年度第二学期“开放专科”期末考试 物流管理专业 物流管理定量分析基础 试题 200 年 7月 题 号 四 总 分 分 数 登_创些兰全 一、单项选择题 (每小题 4分 ,共 20分) }.若某物资的总供应) }3}.大于总需求量 ,则可增设一个( ),其需求量取总供应 量与总 需求量 的差额 ,并取各产地到该销 地的一单位运价 为 。,可将不平衡运 输问题化 为平衡运输问 题 。 A.虚产地 B.虚销地 C.需求量 }}.供应量 min5= 一x,十一3.x:一+一牛r, ‘一二;镇4 二:) 5 2.线性规划问题 的标准形式为( 、一1,x},.x-多C maxS'=x,一3.x:一4x{十O.x、牛Ox。一卡O.x} x:斗一2工:十x;,+xa=4 2.z',一}3x:一长}s -_,x}=J _r:一 ‘了。= 3 x,.::,二 ,、一.,,:。,二;)0 1630

minS=-x1+3x2+4xg+0x4十0x5十0x6 x1+2x2+x3+x4=4 2x1十3x2十x3-x3=5 B. x2-x6=3 x1,x2,x3,x4,x5,x8≥0 maxS'=x1-3x2-4x3+0x4+0x5十0x6 x1十22十x3-x4=4 2x1十3x2十x3+x:=5 C. x2十x6=3 x1,x2,x3,x4,x5,x6≥0 minS=-x1+3x2+4x3十0x4十0xs十0x6 x1十2x2+x3-x4=4 2x1十3x2+x3十x6=5 D. x2-x6=3 x1,x2x3,x4,x6,x6≥0 3.矩阵 的逆矩阵是( )。 A. 0 01 4.设某公司运输某物品的总成本(单位:百元)函数为C(q)=500+2g十q2,则运输量为 100单位时的边际成本为( )百元/单位。 A.202 B.107 C.10700 D.702 5.由曲线y=e,直线x=1,x=2及x轴围成的曲边梯形的面积表示为()。 B.e'dz c. e'dx D.- 1631
minS=一x,+3x2 --4x3 -}-Ox4+Ox, +0x6 x,+2 x2+ x,十x,=4 2x,+ 3x2+x3一x}=5 x2一x6=3 x x2,x3,x4,x,,x6)0 一 之 .| 、 maxS‘=x,一3x:一4x3 +0x4 -{-Ox} -f-Oxs x,+2x2+x3一x4=4 2 x,+3x:十一x,+x,=J x2+x6=3 x x2 ,x;x x, ,x6,0 了1 | 之、 | | minS=一x, -3x2+4x3 +0x4 }-Ox,十0x6 x1 +2x2十x3一x4=4 2x1十3x2 -f-x3 }-x,=5 x2一x6=3 二工,二:,x3,二;,二5,二6,0 一 了一 胜 ﹃ ! 1 1 .l e e l 八 ︺ 11 , . 1 , . J 尸| 之 3.矩阵 的逆矩阵是( ) 门 J.es wel 一 n︺ 11 ﹃. 1 1.1 干 . 一 且 ﹃一 引 , 1 动. 1 j.土 八州 U -! .|l lL . 一| .||| |曰 1 - 一 . D. 十 一 1 」 d | | 阳 . C. 4.设某公 司运输某物品 100单位时的边际成本为( 的总成本(单位:百元)函数为C (q>二500-}2q}-了,则运输量为 )百元/单位。 A. 202 C. 10700 107 702 由曲线y-er,直线x= “·{:2zC}.T C.丁一dx 1,二=2及 二轴围成的曲边梯形的面积表示为( X J U e 厂 ! ‘ . B {e' dx 1631

得分 评卷人 二、计算题(每小题7分,共21分) a- 01 6. ,求:AB+2B。 7.设y=x2e,求:y。 8.计算定积分:(2x+)dx 得 分 评卷人 三、编程题(每小题6分,共12分)】 9.试写出用MATLAB软件计算函数y=e+1一In(2x)的二阶导数的命令语句。 10.试写出用MATLAB软件计算定积分 √x+2dx的命令语句。 得 分 评卷人 四、应用题(第11、12题各14分,第13题19分,共47分) 11.运输某物品q百台的成本函数为C(q)=4g2+200(万元),收人函数为 R(g)=100q一q(万元),问:运输量为多少时利润最大?并求最大利润。 12.某物流公司下属企业在一个生产周期内生产甲、乙两种产品,这两种产品分别需要 A,B,C,D四种不同的机床来加工,这四种机床的可用工时分别为1500,1200,1800,1400。每 件甲产品分别需要A,B,C机床加工4工时、2工时、5工时;每件乙产品分别需要A,B,D机 床加工3工时、3工时、2工时。又知甲产品每件利润6元,乙产品每件利润8元。试建立在上 述条件下,如何安排生产计划,使企业生产这两种产品能获得利润最大的线性规划模型,并写 出用MATLAB软件计算该线性规划问题的命令语句。 1632
得 分 评 卷人 二、计算题 (每小题 7分 ,共 21分) 」,求:““}- 213。 1 1 C乙 一 一 厂 .l e L B -一 , 门 ! leeeJ 尽 胜|卜 口 -一 已 知 A 7.设 .Y - xz e},求 : 2、 仁乙x 十 — 夕dX 。 广 ! 8.计算定积分:J 得 分 评卷人 三、编程题(每小题 6分 ,共 12分) 9.试写出用MATLAB软件计算函数.v=犷+' -ln(2x)的二阶导数的命令语句。 .试写出用MATLAB软件计算定积分{卜/x ' + 2} dx的命令语句· 得 分 评卷人 四、应用题 (第 11,12题各 14分 ,第 13题 19分,共 47分 ) 11.运输 某 物 品 4百 台 的成 本 函数 为 C(q)= 4了 -f- 200(万元 ),收 人 函数 为 R(妇=100q-了(万元),问:运输量为多少时利润最大?并求最大利润。 12.某物流公司下属企业在一个生产周期内生产甲、乙两种产品,这两种产品分别需要 A,B,C,D四种不同的机床来加工,这四种机床的可用工时分别为 1500,1200,1800,1400。每 件甲产品分别需要 A,B,C机床加工 4工时、2工时、.J工时;每件乙产品分别需要 A,13, U机 床加工 3工时、3工时、2工时。又知甲产品每件利润 6元,乙产品每件利润 8元。试建立在上 述条件下 ,如何安排生产计划 ,使企业生产这两种产品能获得利润最大的线性规划模型 ,并写 出用MATLAB软件计算该线性规划问题的命令语句。 1632

13.某公司从三个产地A1,A2,A,运输某物资到三个销地B,,B2,B,各产地的供应量 (单位:吨)、各销地的需求量(单位:吨)及各产地到各销地的单位运价(单位:百元/吨)如下表 所示: 运输平衡表与运价表 销地 Bu B2 B 供应量 b B2 B3 产地 Ar 60 5 4 1 A2 100 8 9 2 A 140 4 3 6 需求量 140 110 50 300 (1)在下表中写出用最小元素法编制的初始调运方案: 运输平衡表与运价表 销地 B Ba B 供应量 B B2 B 产地 A 60 5 4 1 A2 100 8 9 2 A 140 4 6 需求量 140 110 50 300 (2)检验上述初始调运方案是否最优,若非最优,求最优调运方案,并计算最低运输总费 用。 1633
13.某公司从三个产地 A Az,A;、运输某物资到三个销地 Bi,B2,Bs,各产地的供应量 (单位:吨)、各销地的需求量(单位:吨)及各产地到各销地的单位运价(单位:百元/吨)如下表 所示: 运输平衡表与运价表 几拌 B, B2 B, I 供应量 一UZ B, Al 60 {5 4 1 AZ 100 {8 9 2 A} 140 {4 3 6 需求量 140 110 50 300 (1)在下表中写出用最小元素法编制的初始调运方案: 运输平衡表与运价表 \产\地\} \ } \ 地 \ B1 B: B。 供应一B、 U2 B, AC }} 一5 4 1 A2 100 一8 9 2 A_} 140 4 3 6 需求量 140 110 50 300 } (2)检验上述初始调运方案是否最优,若非最优,求最优调运方案,并计算最低运输总费 1633

试卷代号:2320 中央广播电视大学2006一2007学年度第二学期“开放专科”期末考试 物流管理专业物流管理定量分析基础试题答案及评分标准 (供参考) 2007年7月 一、单项选择题(每小题4分,共20分) 1.B 2.A 3.D 4.A 5.C 二、计算题(每小题7分,共21分) 6.A8+2B= ETECE 7分 7.y'=(x2)'·e+x2·(e2)'=(2x+x2)e* 7分 8.(2x+2)dr=(x+21nlx)=3+21h2 7分 三、编程题(每小题6分,共12分) 9. >>clear; >>syms x y; 2分 >>y=exp(x2+1)-log(2*x): 4分 >>dy=diff(y,2) 6分 10. >clear; >>syms x y; 2分 >>y=sqr1(x3+2x); 4分 >>int(y,1,4) 6分 1634
试卷代号:2320 中央广播电视大学2006-2007学年度第二学期“开放专科”期末考试 物流管理专业 物流管理定量分析基础 试题答案及评分标准 (供参考) 200?年 z月 一、单项选择题(每小题 4分,共 20分) 1.B 2. A 3. D 4.A 5. C 二、计算题(每小题 7分,共 21分) 分 分 ︻丫 一丫 ﹁ les lwe l |eJ 八︹ 0曰 一 10 广 !十 十 1 一一 ﹃ ! 一 ﹂ ︵0 月任 一 2 一 12 一 4 厂 | l we weL + 门 f 、l es吸 I esJ O U 月任 -| l leJ 八曰 月任 广 ! ! | L 十 ﹃ | l we -J 八曰 月任 9 ︺ 月任 一 一 广 1 1 十 ﹂ ﹁.|1 习 0 曰 ,1 6. AB-}-2B= 一 2 一 4 =( x2)‘·e} -t- xu·( e})‘=(2x-}-x2 )e} 2、, X , lGx 十 一 夕ax = x (x2+ 21n = 3十 21n2 7分 "y 产十 ﹂ ︹了 O U 三、编程题 (每小题 6分 ,共 12分) n uclear; 分 分 分 9 户 ‘斗 ︸卜 >> syms x y; ; y=exp(x'2+1)一log>dy=diff(y,2) to ; clear, 分 分 分 0乙 刁斗 内卜 ︶ >> syms x y; }?Y二sgrt(x'3-f-2"x); >>int(y} 1,4) 1634

四、应用题(第11、12题各14分,第13题19分,共47分) 11.利润函数L(g)=R(q)-C(g)=100g-5g2一200 6分 令边际利润ML(q)=100-10g=0,得惟一驻点g=10(百台) 11分 故当运输量为10百台时,可获利润最大。最大利润为L(10)-300(万元) 14分 12.设生产甲、乙两种产品的产量分别为x1件和x2件。显然,x1,x≥0 1分 maxS=6x1+8x2 4x1+3x2≤1500 2x1+3.x2≤1200 线性规划模型为: 8分 5.x1≤1800 2x2≤1400 x:,x2≥0 计算该线性规划模型的MATLAB语句为: >clear; >>C=-[68]: >>A=[43:23:50:02]: 10分 >>B=[1500:1200;1800:1400]: >>LB=[0:0]: 12分 >>[X,fval,exitflag]=linprog(C,A,B,[]],LB) 14分 13.用最小元素法编制的初始调运方案如下表所示: 运输平衡表与运价表 销地 BI B2 B3 供应量 BI 1B2 B3 产地 Al 10 50 60 5 4 1 A2 100 100 8 9 2 A3 30 110 140 3 6 需求量 140 110 50 300 12分 1635
四、应用题 (第 11,12题各 14分,第 13题 19分 ,共 47分) 11.利润函数L钩)=R(q) -C(q) =100q-5q2 -200 令边际利润 MI A=巨43;23;50;0 2]; >>I3=仁1500;1200;1800;1400]; >>L13=巨。;0]; >>巨X,foal,exitflag口=linprog(C,/A,F3,[],巨】,LI3) 13.用最小元素法编制 的初始调运方案 如一下表所示: 运输平衡表与运价表 6乡全 11分 14乡于 1分 8乡全 10乡全 12乡于 1牛分 1 1 | | J vl es re! | we l 12分 )63 }}
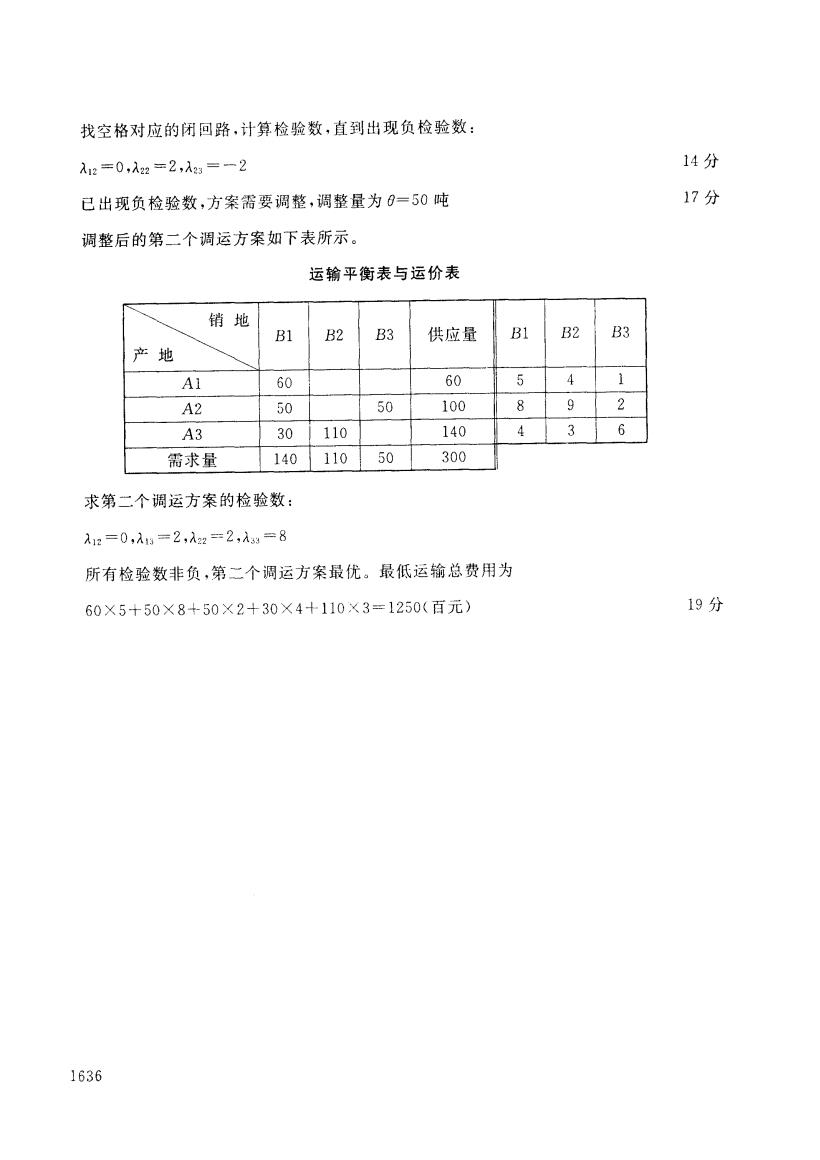
找空格对应的闭回路,计算检验数,直到出现负检验数: 入12=0,λ22=2,λ23=一2 14分 已出现负检验数,方案需要调整,调整量为0=50吨 17分 调整后的第二个调运方案如下表所示。 运输平衡表与运价表 销地 B1 B2 B3 供应量 B1 B2 B3 产地 Al 60 60 5 4 1 A2 50 50 100 8 9 2 A3 30 110 140 4 3 6 需求量 140 110 50 300 求第二个调运方案的检验数: 112=0,入13=2,入22=2,A33=8 所有检验数非负,第二个调运方案最优。最低运输总费用为 60×5+50×8+50×2+30×4+110×3=1250(百元) 19分 1636
找空格对应的闭回路 ,计算检验数 ,直到出现负检验数 : },z =O,}lzz =2八z3=一2 已出现负检验数,方案需要调整,调整量为 B= 。吨 调整后的第二个调运方案如下表所示 。 运输平衡表与运价表 24分 17分 }产\地 } \ }、\ 地B1 B2 B3 供应量 一E32 B3 Al 60.i 60 }5 4 1 A2 }0 50 100 一 9 2 A3 30 110 140 一4 3 6 需求量 140 110 50 300 求第二个调运方案的检验数: 又12今0,久1:、=2+}zz=Z,}1s3“8 所有检验数非负 ,第二个调运方案最优。最低运输总费用为 60X5十50X8斗一50X2斗30X4斗一110;'C3=1250(百元) 19分 1636