
Chapter 3 Kinetic Models
Kinetic Models Chapter 3
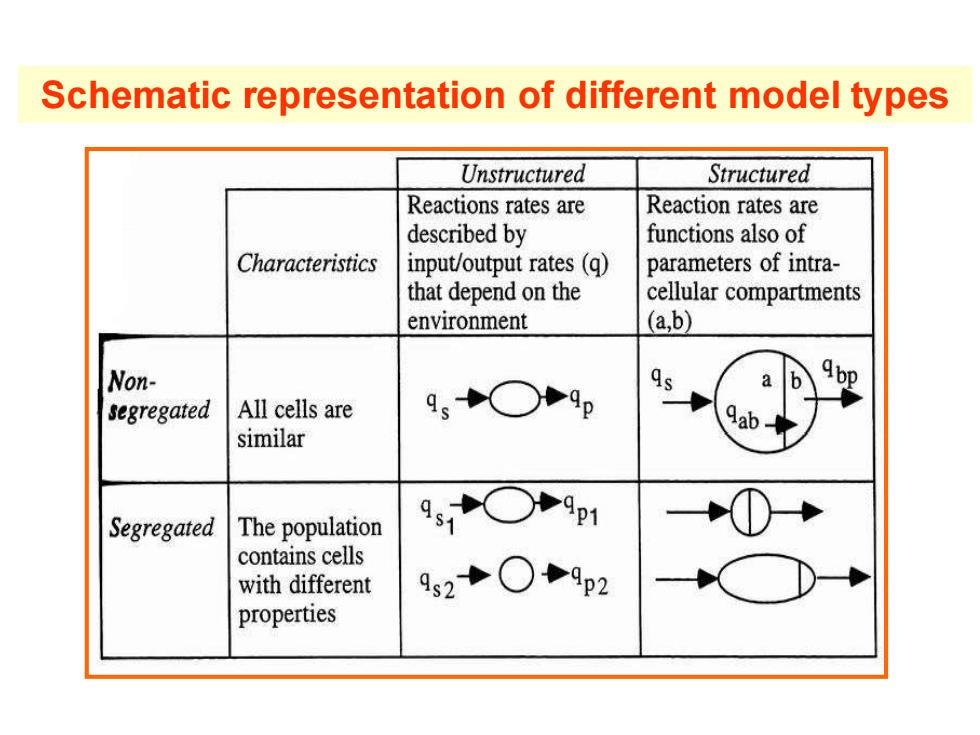
Schematic representation of different model types Unstructured Structured Reactions rates are Reaction rates are described by functions also of Characteristics input/output rates(q) parameters of intra- that depend on the cellular compartments environment (a,b) Non- 9○P9p a segregated All cells are similar Segregated The population 91○P9p1 contains cells with different 92+○9p2 properties
Schematic representation of different model types

3.1.A general mass balance of the reactor Time Ut+At slope= dy/dt ←—△t→ t+△t Euler's method to solve a first order differential equation to calculate how the variable y varies with time t.Initial values ofy and t must be known.The t-scale is then divided into very small intervals(At) so that the slope dy/dt can be condidered practically constant in the interval t to t+At.The value ofy at the end of this interval is then obtained as yt+At=yt+t*dy/dt.The new values tAt and ytAt are then used as initial values for the next calculation.The time interval illustrated in the figure above is oversized.For simulation of a typical batch process the time interval is usually in the range of one second or below
3.1. A general mass balance of the reactor

Q0+9g,0 A perfectly mixed reactor with medium volume V and the concentration y of a component in 9 the reactor.Medium flow rates are designated as F and gas flow rates as O,respectively.Concentrations in gas are labelled with subscript g. Subscripts i and o refer to parameters of inlet and outlet V y flows,respectively.A separation factor, 6, specifies the concentration of y in the outlet medium. Qi yg,i Change=Input -Outlet +Reaction d(Vy)=Fy+Qys.-Fo-Qoys.0+Vry dt Where ry is the volumetric reaction rate (kg m-3 h-1)for production (ry>O)or consumption(ry<O)of the component y
Change = Input -Outlet +Reaction Fiyi Qiyg i F y Q yg Vry dt d Vy = + , − 0 − 0 ,0 + ( ) Where ry is the volumetric reaction rate (kg m-3 h -1 ) for production (ry >0)or consumption (ry <0) of the component y

a2=r()+() dⅣ=F:-Fo d We can obtaina general mass balance equation that describes the change of y with time 命=0-0+0-8++号鲁
( ) dt y dV dt dy V dt d Vy + = ( ) Fi Fo dt dV = − g o o g i i y y o i i y V Q y V Q y r V F y y V F dt dy = ( − ) + ( − ) + + , − , We can obtain a general mass balance equation that describes the change of y with time

3.2.Biological reaction rate models Volumetric reaction rate,r(kg m-3 h-1) r=gX Where q is a certain specific rate(kg kg) X is the concentration of the biocatalyst(kg m3) The specific(q)and volumetric(r)reaction rates are further specified by subscripts 4s and rs A limiting substrate qs2 and rs2 A non-limiting substrate qo and ro oxygen gp and rp product gx (mostly written u)and rx biomass
Volumetric reaction rate, r (kg m-3 h-1) Where q is a certain specific rate (kg kg-1 h -1 ) X is the concentration of the biocatalyst (kg m-3 ) qs and rs A limiting substrate qs2 and rs2 A non-limiting substrate qo and ro oxygen qp and rp product qx (mostly written μ) and rx biomass 3.2. Biological reaction rate models r=qX The specific (q) and volumetric (r) reaction rates are further specified by subscripts
Model >Substrate consumption model >Cell growth model >Product formation model
Model ➢Substrate consumption model ➢Cell growth model ➢Product formation model

① Substrate consumption Monod model S gs=gs.m S+Ks u=u max S S+Ks Competitive inhibition: S gs =g9s.mx S+Ks(1+1/Ki) Non-competitive inhibition as,max S 9s= (1+I/Ki)S+Ks
① Substrate consumption s s s S K S q q + = , max S Ks S + = max (1 / ) , max i s s S Ks I K S q q + + = S Ks S I Ki q q s s + + = (1 / ) , max Monod model Competitive inhibition: Non-competitive inhibition
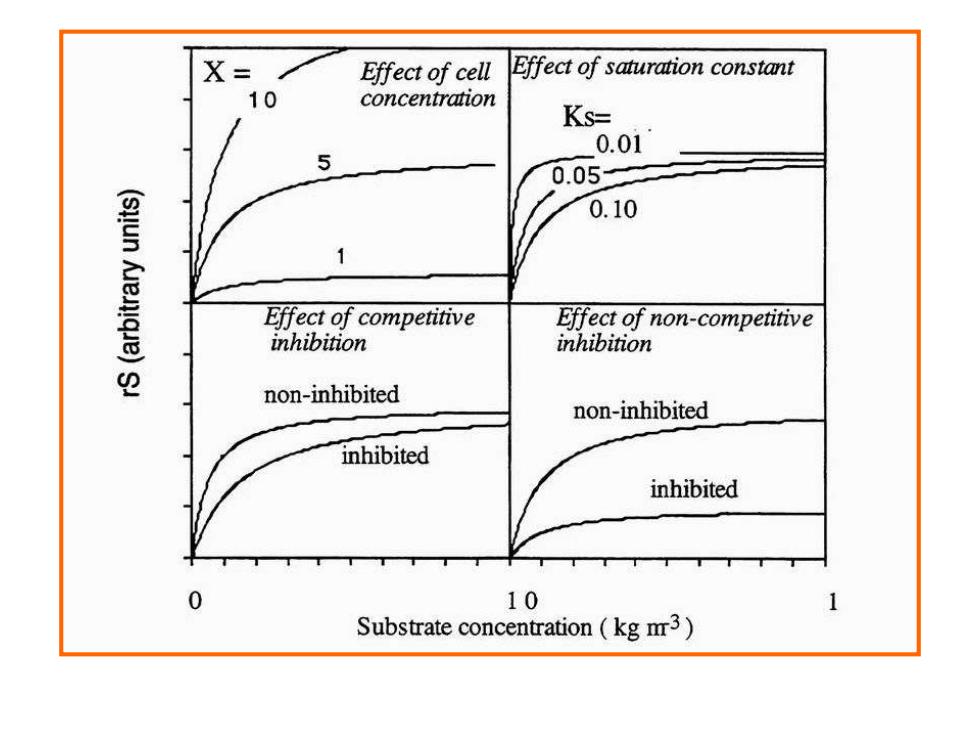
X= Effect of cell Effect of saturation constant 10 concentration Ks= 0.01 0.05 0.10 Effect of competitive Effect of non-competitive inhibition inhibition non-inhibited non-inhibited inhibited inhibited 0 10 Substrate concentration(kg m3)

cell growth and biomass yield rx=uX u=gs Yx/s H=dX I dt X where Yx/s (kg kg-1)is the yield coefficient Substrate Product Yield coefficient(kg kg-1) Carbohydrate 1) Cells 0.5 Carbohydrate 2) Cells 0.7 Carbohydrate 3) Cells 0.1 Hydrocarbon Cells 1 Methanol Cells 0.5 Oxygen Cells 1 Oxygen Cells 5) 0.3 Glucose Ethanol 0.45 Sucrose Citric acid 0.9 Glucose Penicillin 0.08 1)Aerobic metabolism with ammonia as N-source 2)Aerobic metabolism with amino acids as N-source 3)Anaerobic metabolism 4)With carbohydrate as energy source 5)With hydrocarbon as energy source
② cell growth and biomass yield dt X dX 1 = Substrate Product Yield coefficient (kg kg-1 ) Carbohydrate 1) Cells 0.5 Carbohydrate 2) Cells 0.7 Carbohydrate 3) Cells 0.1 Hydrocarbon Cells 1 Methanol Cells 0.5 Oxygen Cells 4) 1 Oxygen Cells 5) 0.3 Glucose Ethanol 0.45 Sucrose Citric acid 0.9 Glucose Penicillin 0.08 1) Aerobic metabolism with ammonia as N-source 2)Aerobic metabolism with amino acids as N-source 3) Anaerobic metabolism 4) With carbohydrate as energy source 5)With hydrocarbon as energy source rx=μX μ=qs Yx/s where Yx/s (kg kg-1) is the yield coefficient