
金融随机分析 课程名称:金融随机分析Stochastic Analysis for Finance 课程性质:选修 学分课时:2学分,32课时 主讲教师:邓军助理教授 所属院系:金融学院金融工程系 电话:64493331,E-mail:jundeng(@uibe.edu.cn 教学对象:全校本科生 学术诚信:本课程对于学生的学术诚信的要求遵从《对外经济贸易大学学生违纪处分条例》、《对外经济贸易大学学生 学习违纪处分实施细则》、《对外经济贸易大学考场纪律》的规定。 考核方式:平时作业成绩 期末考试,闭卷考试,笔试。 其中平时成绩占40%,期末考试占60% 出勤要求:遵从《对外经济贸易大学本科生课堂学习规范》,要求学生关闭一切电子设备;不能 无故缺席上课;上课专心听讲,积极参与课堂讨论;课后认真复习课堂上讲授内容,独立完成教 师布置的任务;并预习新课。学生缺勤不得多于总课时的四分之一。教师可以根据考勤情况决定 学生是否可以参加考试、是否扣分。 先修课程:高等数学、概率论 课程简介 随机分析是战后兴起并蓬勃发展的一门崭新学科,根植于二十世纪的泛函分析与概率论理论基础,随着tO随机积分的 构造而确立学科地位,后于1973年的Black-Sholes期权定价公式引发的“第二次华尔街革命”达到鼎盛,至今仍在世界金融市场体系 与学术研究中被广泛应用。对于金融工程专业的本科生而言,拥有坚实的随机分析基础知识,对于面向工业界还是学术界的求职与后 续职业发展,均为必要。本课程整理随机分析的理论脉络与金融应用,立足于严格的数学推导论证,也兼顾介绍实践应用。通过介绍 布朗运动、to随机积分、风险中性测度的构造与金融意义,使学生掌握随机分析领域的数学基础及其缘由,具备相关领域求职应聘与 申请深造时所需的知识技能,并了解随机分析理论在金融应用中的作用。 二、教学目标 本课程的定位是:讲解随机分析在金融中应用的基础知识,提高学生分析问题的能力 三、课程资料 1、教材:无指定教材 2、参考资料: Stochastic Calculus for Finance ll:Continuous Time Models,Steven Shreve,2004. 2.Stochastic Calculus for Finance I:The Binomial Asset Pricing Model(Springer Finance),Steven Shreve,2004. Notes on Stochastic Finance,Nicolas Privault,2013,http://www.ntu.edu.sg/home/nprivault/indext.html Stochastic Finance:An Introduction in Discrete Time,Hans Follmer,Alexander Schied,Walter de Gruyter,2004. Essentials of Stochastic Finance:Facts,Models,Theory,Albert N.Shiryaev and N.Kruzhilin,World Scientific Pub,1999. 其他参考资料随课程内容安排 四、学习效果及达成途径 1.学习效果 通过本课程的学习,希望达成的学习效果如下: 了解随机分析的基础理论框架 应该应用随机分析知识进行简单理论推导 对简单金融产品能够定价 2达成学习效果的途径 上课跟着老师思路走;课后完成相应的作业;认真准备期末考试。 五、教学进度计划表 本课程教学周为16周,具体安排如下: 周次 内容提要 阅读材料 作业与考试 1 课程介绍 教学内容 2 概率论基础知识:概率空 间 Notes on Stochastic Finance 教学内容 慨率论基础知识:随机变 3 量和数学期望 Notes on Stochastic Finance 教学内容 Essentials of Stochastic 随机过程知识:Sigma代 4 数,代数流 Finance:Facts,Models, 教学内容 Theory
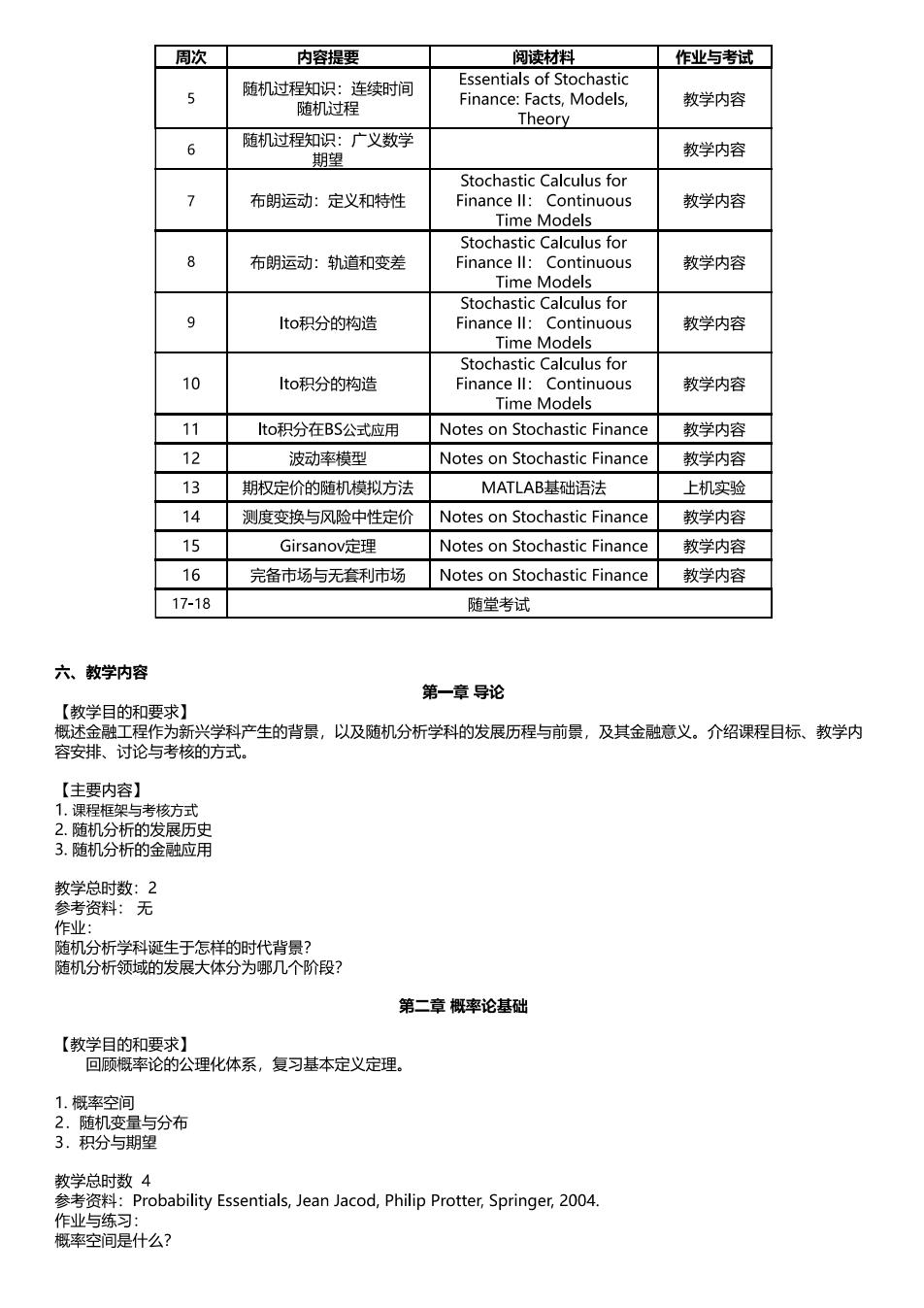
周次 内容提要 阅读材料 作业与考试 随机过程知识:连续时间 Essentials of Stochastic 随机过程 Finance:Facts,Models, 教学内容 Theory 6 随机过程知识:广义数学 期望 教学内容 Stochastic Calculus for 7 布朗运动:定义和特性 Finance ll:Continuous 教学内容 Time Models Stochastic Calculus for 8 布朗运动:轨道和变差 Finance ll:Continuous 教学内容 Time Models Stochastic Calculus for 9 Ito积分的构造 Finance ll:Continuous 教学内容 Time Models Stochastic Calculus for 10 Ito积分的构造 Finance ll:Continuous 教学内容 Time Models 11 to积分在BS公式应用 Notes on Stochastic Finance 教学内容 12 波动率模型 Notes on Stochastic Finance 教学内容 13 期权定价的随机模拟方法 MATLAB:基础语法 上机实验 14 测度变换与风险中性定价 Notes on Stochastic Finance 教学内容 15 Girsanov定理 Notes on Stochastic Finance 教学内容 16 完备市场与无套利市场 Notes on Stochastic Finance 教学内容 17-18 随堂考试 六、教学内容 第一章导论 【教学目的和要求】 概述金融工程作为新兴学科产生的背景,以及随机分析学科的发展历程与前景,及其金融意义。介绍课程目标、教学内 容安排、讨论与考核的方式。 【主要内容】 1.课程框架与考核方式 2.随机分析的发展历史 3.随机分析的金融应用 教学总时数:2 参考资料:无 作业: 随机分析学科诞生于怎样的时代背景? 随机分析领域的发展大体分为哪几个阶段? 第二章概率论基础 【教学目的和要求】 回顾概率论的公理化体系,复习基本定义定理。 1.概率空间 2.随机变量与分布 3.积分与期望 教学总时数4 参考资料:Probability Essentials,Jean Jacod,Philip Protter,,Springer,2004. 作业与练习: 概率空间是什么?

随机变量是什么? 随机变量的积分和一般函数的积分有哪些区别和联系? 第三章信息与条件期望 【教学目的和要求】 基于连续时间随机过程知识,详细讲解域流、条件期望、停时等概念。 1.连续时间随机过程 2.信息与域流 3.一般条件期望 4.有限维分布族与修正过程 教学总时数4 参考资料:Probability Essentials,,Jean Jacod,Philip Protter,,Springer,,2004. 作业与练习:: 域流的定义是什么?它的含义是什么? 一般条件期望是一个数吗?请举例说明。 有限维分布族相同的随机过程,是否一定互为修正?证明或举出反例。 第四章布朗运动 【教学目的和要求】 理解布朗运动的定义和性质,以及Lvy刻画定理。了解均方有界变差过程的特点。对布朗运动的广泛应用形成印象。 随机游动及其极限 布朗运动的定义与简单性质 Ley刻画定理 平方有界变差过程 反射原理 教学总时数4 参考资料: Stochastic Calculus for Finance ll:Continuous Time Models,Steven Shreve,2004 Essentials of Stochastic Finance:Facts,Models,Theory 作业与练习: 叙述布朗运动的定义 证明反射原理 计算 第五章随机分析与随机微分方程 【教学目的和要求】 在比照普通Riemann积分的基础上,构造to随机积分,并阐释其鞅性质与金融意义,为金融衍生工具定价理论建立理论基 础。理解随机微分方程的形式,熟练掌握to引理。掌握一定的数值模拟与计算方法,并进行实践操作。 1.从简单被积函数到一般被积函数 2.to积分的金融意义 3.定义:从积分形式到微分形式 4.to引理及其应用 5.Black-Sholes模型 6.其它波动率模型与金融意义 7.期权定价的随机模拟方法(MATLAB.上机实验或演示) 教学总时数10 Stochastic Calculus for Finance ll:Continuous Time Models Black,Fischer,and Myron Scholes."The pricing of options and corporate liabilities."The journal of political economy(1973):637-654. Essentials of Stochastic Finance:Facts,Models,Theory Note on Stochastic Finance 作业与练习: t0积分与普通积分的主要区别是什么? Black-Scholes模型具有哪些优良性质?

请使用随机模拟方法为Black-Scholes模型下的欧式看涨期权定价。 第六章测度变换与风险中性定价 【教学目的和要求】 掌握连续时间欧式期权在Black-Sholes模型下的风险中性定价,了解Black-Sholes模型的缺陷、厚尾现象和市场参数校准。 对随机分析理论的金融应用建立比较全面的认识。 1.Radon-Nikodym:导数 2.Girsanov定理 3.风险中性测度与期权定价 4.完备市场与无套利市场 5.市场流动性与参数校准 6.其它结构化产品 教学总时数6 Stochastic Calculus for Finance ll:Continuous Time Models Essentials of Stochastic Finance:Facts,Models,Theory Note on Stochastic Finance 作业与练习: Black-Scholes模型下如何进行风险测度变换? 无套利市场有哪些特征? 为什么我们要进行市场参数校准?