
第二章用网络等效简化电路分析 当电路规模比较大时,建立和求解电路方程都比较困 难,此时,可以利用网络等效的概念将电路规模减小,从 而简化电路分析。当我们对某个负载电阻或电阻单口网络 的电压,电流和电功率感兴趣,如图2-1(a)所示,可以用 单口网络的等效电路来代替单口网络,得到图2-1(b)和(c) 所示的电阻分压电路和分流电路,从而简化电路的分析。 a 含源 线性 岛商 单口 网络 网 b (a) (b) (c) 图2-1
第二章 用网络等效简化电路分析 当电路规模比较大时,建立和求解电路方程都比较困 难,此时,可以利用网络等效的概念将电路规模减小,从 而简化电路分析。当我们对某个负载电阻或电阻单口网络 的电压,电流和电功率感兴趣,如图2-1(a)所示,可以用 单口网络的等效电路来代替单口网络,得到图2-1(b)和(c) 所示的电阻分压电路和分流电路,从而简化电路的分析。 图2-1

本章介绍利用网络等效概念简化电路分析的一些方法 先讨论电阻分压电路和分流电路,再介绍线性电阻单口 网络的电压电流关系及其等效电路,然后讨论电阻星形 联结联接和三角形联结的等效变换,最后讨论简单非线 性电阻电路的分析。 §2-1电阻分压电路和分流电路 本节通过对常用的电阻串联分压电路和电阻并联分 流电路的讨论,导出电阻串联的分压公式和电阻并联 的分流公式,并举例说明它的使用
本章介绍利用网络等效概念简化电路分析的一些方法, 先讨论电阻分压电路和分流电路,再介绍线性电阻单口 网络的电压电流关系及其等效电路,然后讨论电阻星形 联结联接和三角形联结的等效变换,最后讨论简单非线 性电阻电路的分析。 §2-1电阻分压电路和分流电路 本节通过对常用的电阻串联分压电路和电阻并联分 流电路的讨论,导出电阻串联的分压公式和电阻并联 的分流公式,并举例说明它的使用

一、电阻分压电路 对图2-2所示两个电阻串联的分压电路进行分析,得 出一些有用的公式。 Ri i 图2-2 对图2-2所示电阻串联分压电路列出KCL方程 i=i,=2 列出KVL方程 W=W1+2
一、电阻分压电路 对图 2-2所示两个电阻串联的分压电路进行分析,得 出一些有用的公式。 图 2-2 对图2-2所示电阻串联分压电路列出KCL方程 1 2 i = i = i 列出KVL方程 u = u1 + u2

列出电路元件的VCR方程 u=us 41=Ri1 42=R22 将电阻元件的欧姆定律代入KVL方程,得到电流的计算 公式 4s=41+u2FRi+R2i2=(R1+R2)i i- us R1+R2 将它代入电阻元件的欧姆定律,得到计算电阻电压的分 压公式 R R2 R+R s R+R2 s
列出电路元件的VCR方程 S 1 1 1 2 2 2 u = u u = R i u = R i 将电阻元件的欧姆定律代入KVL方程,得到电流i的计算 公式 1 2 S S 1 2 1 1 2 2 1 2 ( ) R R u i u u u R i R i R R i + = = + = + = + 将它代入电阻元件的欧姆定律,得到计算电阻电压的分 压公式 S 1 2 2 S 2 1 2 1 1 u R R R u u R R R u + = + =

般来说,个电阻串联时,第k个电阻上电压可按 以下分压公式计算 (21) k=1 电阻串联分压公式表示某个电阻上的电压与总电压 之间的关系。分压公式说明某个电阻电压与其电阻值成 正比例,电阻增加时其电压也增大。 值得注意的是电阻串联分压公式是在图2-2电路所 示的电压参考方向得到的,与电流参考方向的选择无关 当公式中涉及的电压变量4或s的参考方向发生变化时, 公式中将出现一个负号
一般来说,n个电阻串联时,第k个电阻上电压可按 以下分压公式计算 (2 1) S 1 u - R R u n k k k k = = 电阻串联分压公式表示某个电阻上的电压与总电压 之间的关系。分压公式说明某个电阻电压与其电阻值成 正比例,电阻增加时其电压也增大。 值得注意的是电阻串联分压公式是在图2-2电路所 示的电压参考方向得到的,与电流参考方向的选择无关, 当公式中涉及的电压变量uk或uS的参考方向发生变化时, 公式中将出现一个负号

例2-1电路如图2-3所示,求R=02,42,122,∞时的电压Ub° 62 2 图2-3 解:利用电阻串联分压公式可以求得电压U和Uc 602 122 Ua心 ×8V=6V x8V 2Ω+62 12Ω+R 将电阻R之值代入上式,求得电压V后,再用KVL求得 Uab,计算结果如下所示:
例2-1 电路如图2-3所示,求R=0,4,12,∞时的电压Uab。 图2-3 解: 利用电阻串联分压公式可以求得电压Uac和Ubc 8V 12 12 8V 6 V 2 6 6 a c bc + = = + = R U U 将电阻R之值代入上式,求得电压Ubc后,再用KVL求得 Uab,计算结果如下所示:

2 62 122 R 0Ω 4Ω 12Ω2 00 6V 6V 6V 6V 8V 6V 4V 0V Uab=Uac一Ubc -2V 0 2V 6V 由计算结果可见,随着电阻的增加,电压U逐渐减 小,电压U由负变正,说明电压U的实际方向可以随着 电阻的变化而改变
R 0 4 12 ∞ Uac 6 V 6 V 6 V 6 V Ubc 8 V 6 V 4 V 0 V Uab =Uac-Ubc -2 V 0 2 V 6 V 由计算结果可见,随着电阻R的增加,电压Ubc逐渐减 小,电压Uab由负变正,说明电压Uab的实际方向可以随着 电阻R的变化而改变
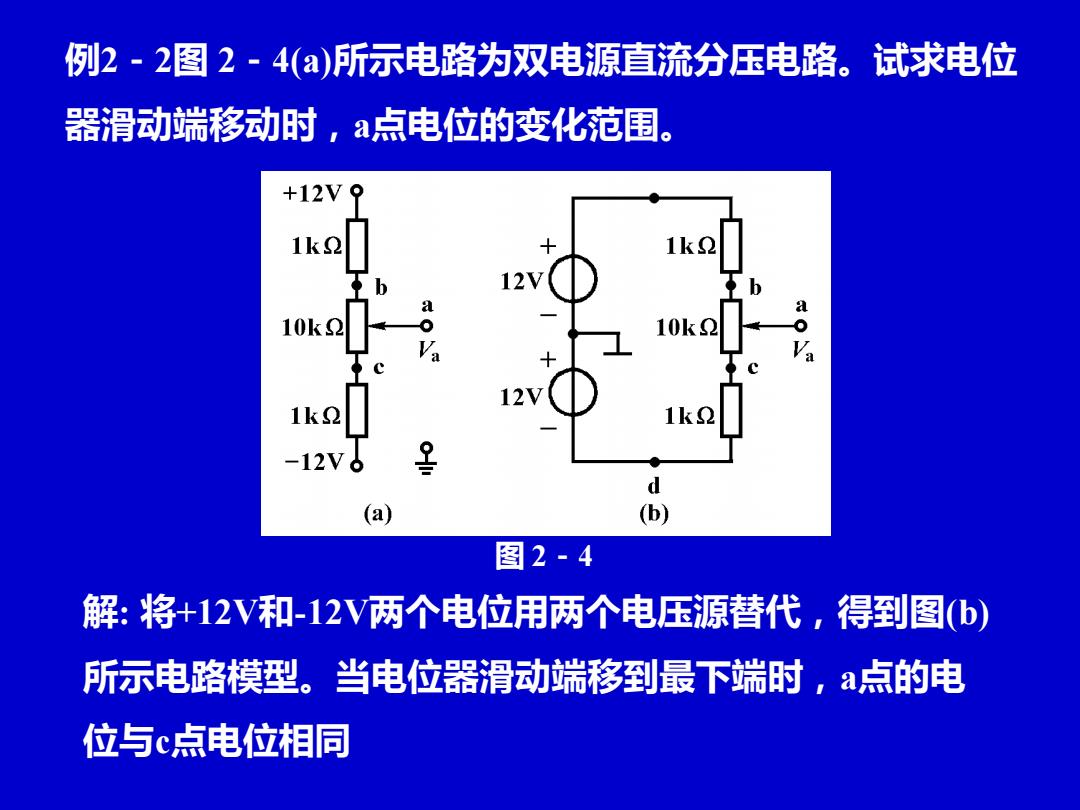
例2-2图2-4(a)所示电路为双电源直流分压电路。试求电位 器滑动端移动时,a点电位的变化范围。 +12V 1k2 1k2 9 10k2 10h 1k2 1k2 -12V (a) (b) 图2-4 解:将+12V和-12V两个电位用两个电压源替代,得到图b 所示电路模型。当电位器滑动端移到最下端时,a点的电 位与c点电位相同
例2-2图 2-4(a)所示电路为双电源直流分压电路。试求电位 器滑动端移动时,a点电位的变化范围。 图 2-4 解: 将+12V和-12V两个电位用两个电压源替代,得到图(b) 所示电路模型。当电位器滑动端移到最下端时,a点的电 位与c点电位相同
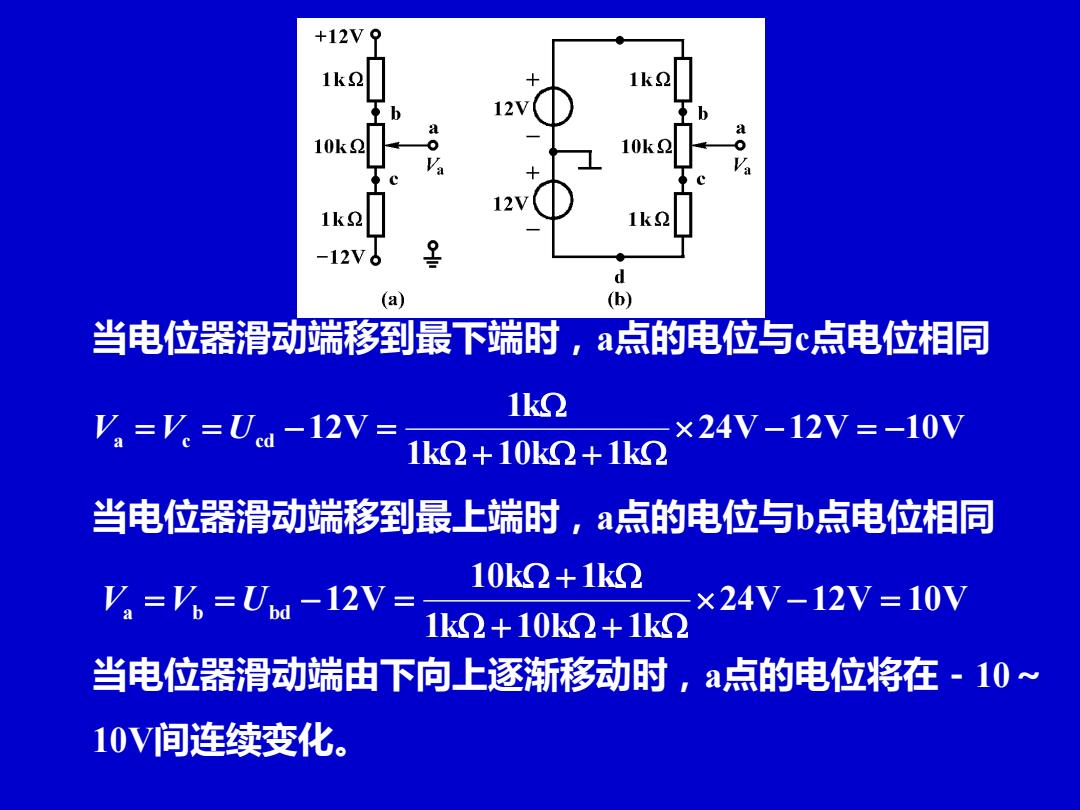
+12V9 1k2 1k0 10k2 10k 1k2 1k2 -12V (a) (b) 当电位器滑动端移到最下端时,a点的电位与c点电位相同 1k④ V=V=Ued-12V= ×24V-12V=-10V 1kΩ+10k④+1kΩ 当电位器滑动端移到最上端时,a点的电位与b点电位相同 10k2+1kΩ Va=Vo=Uid -12V ×24V-12V=10V 1k2+10k2+1kΩ 当电位器滑动端由下向上逐渐移动时,a点的电位将在-10~ 10V间连续变化
当电位器滑动端移到最下端时,a点的电位与c点电位相同 24V 12V 10V 1k 10k 1k 1k a c cd 12V − = − + + V =V = U − = 当电位器滑动端移到最上端时,a点的电位与b点电位相同 24V 12V 10V 1k 10k 1k 10k 1k a b bd 12V − = + + + V =V = U − = 当电位器滑动端由下向上逐渐移动时,a点的电位将在-10~ 10V间连续变化

双电源 电阻分压电路 胡翔骏制作 高等教育出版社 在幻灯片放映时,请用鼠标单击图片放映录像
在幻灯片放映时,请用鼠标单击图片放映录像