
第九章二阶电路分析 由二阶微分方程描述的电路称为二阶电路。 分析二阶电路的方法仍然是建立二阶微分方程, 并利用初始条件求解得到电路的响应。本章主要 讨论含两个动态元件的线性二阶电路,重点是讨 论电路的零输入响应。最后介绍如何利用计算机 程序分析高阶动态电路
第九章 二阶电路分析 由二阶微分方程描述的电路称为二阶电路。 分析二阶电路的方法仍然是建立二阶微分方程, 并利用初始条件求解得到电路的响应。本章主要 讨论含两个动态元件的线性二阶电路,重点是讨 论电路的零输入响应。最后介绍如何利用计算机 程序分析高阶动态电路
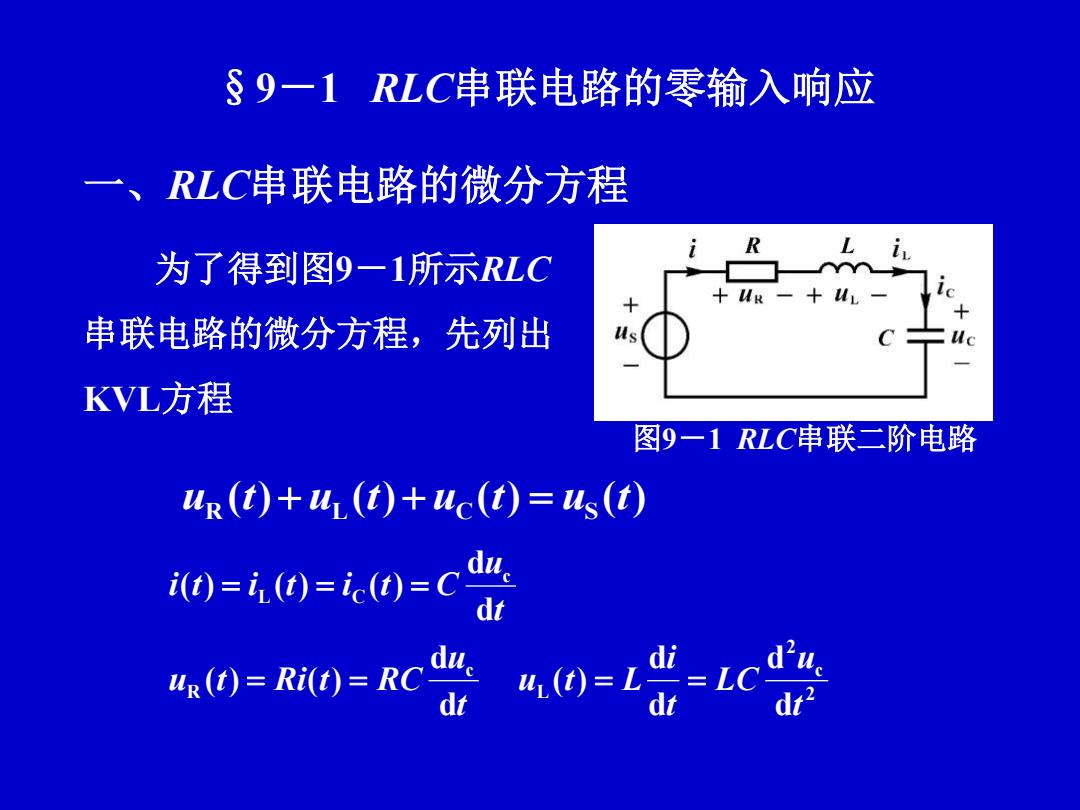
§9一1RLC串联电路的零输入响应 一、RLC串联电路的微分方程 L i 为了得到图9一1所示RLC +u 串联电路的微分方程,先列出 c KVL方程 图9一1RLC串联二阶电路 ur (t)+u (t)+uc(t)=us(t) 0=0-=40=c0 4,0=R0=Rc
§9-1 RLC串联电路的零输入响应 一、RLC串联电路的微分方程 图9-1 RLC串联二阶电路 ( ) ( ) ( ) ( ) R L C S u t u t u t u t 2 c 2 L c R c L C d d d d ( ) d d ( ) ( ) d d ( ) ( ) ( ) t u LC t i u t L t u u t Ri t RC t u i t i t i t C 为了得到图9-1所示RLC 串联电路的微分方程,先列出 KVL方程

根据前述方程得到以下微分方程 (9-1) 这是一个常系数非齐次线性二阶微分方程。 零输入响应方程为 Lcdr+RC+=0 dt2 (9-2) dt 其特征方程为 LCs2+RCs+1=0 (9-3) 其特征根为 R S1,21 2L (9-4)
根据前述方程得到以下微分方程 ( ) (9 1) d d d d C S C 2 C 2 u u t t u RC t u LC 这是一个常系数非齐次线性二阶微分方程。 0 (9 2) d d d d C C 2 C 2 u t u RC t u LC 其特征方程为 1 0 (9 3) 2 LCs RCs 其特征根为 (9 4) 1 2 2 2 1 2 L LC R L R s , 零输入响应方程为

电路微分方程的特征根,称为电路的固有频率。当R, L,C的量值不同时,特征根可能出现以下三种情况 1>2时,p,为不相等的实根。过盟尼借识 2.R=2怎时,、,为两个相等的实根。 临界阻尼 情况。 3.R<乙时,S心,为共轭复数根。欠阻尼情况
电路微分方程的特征根,称为电路的固有频率。当R, L,C的量值不同时,特征根可能出现以下三种情况 1. 时, 为不相等的实根。过阻尼情况。 C L R 2 1 2 s ,s 2. 时, 为两个相等的实根。临界阻尼 情况。 1 2 s ,s C L R 2 3. 时, 为共轭复数根。欠阻尼情况。 C L R 2 1 2 s ,s

二、过阻尼情况 当R>2时, 电路的固有频率s1,S,为两个不相同的 实数,齐次微分方程的解答具有下面的形式 uc(t)=Ke"+Ke (9-5) 式中的两个常数K1,K,由初始条件i(0)和4(0)确定。 uc(0)=K1+K2 (9-6) 对式9一5)求导,再令仁0得到 duc(t)m=Ks+K3S:= (9-7 dt
二、过阻尼情况 当 时,电路的固有频率s 1,s 2为两个不相同的 实数,齐次微分方程的解答具有下面的形式 C L R 2 ( ) e e (9 5) 1 2 C 1 2 s t s t u t K K 式中的两个常数K1,K2由初始条件iL (0)和uc (0) 确定。 (0) (9 6) uC K1 K2 对式(9-5)求导,再令t=0得到 (9 7) (0) d d ( ) L 0 1 1 2 2 C C i K s K s t u t t

求解以上两个方程,可以得到 w0-] -] 由此得到电容电压的零输入响应,再利用KCL方程和 电容的VCR可以得到电感电流的零输入响应
求解以上两个方程,可以得到 C i s u s s K C i s u s s K (0) (0) 1 (0) (0) 1 L 1 C 1 2 2 L 2 C 2 1 1 - = - = 由此得到电容电压的零输入响应,再利用KCL方程和 电容的VCR可以得到电感电流的零输入响应

例9-1电路如图9-1所示,已知R=32,L=0.5H,C=0.25F, 4c(0)=2V,(0)=1A,求电容电压和电感电流的零输 入响应。 32 0.5Hi ic 0.25F 图9一1RLC串联二阶电路 解:将R,L,C的量值代入式(9一4)计算出固有频率 R S12= 2L
例9-1 电路如图9-1所示,已知R=3,L=0.5H, C=0.25F, uC (0)=2V, iL (0)=1A,求电容电压和电感电流的零输 入响应。 4 2 3 3 8 3 1 1 2 2 2 2 1 2 L LC R L R s , 解:将R,L,C的量值代入式(9-4)计算出固有频率 图9-1 RLC串联二阶电路

将固有频率、=-2和s2-4代入式(9一5)得到 uc(t)=Kje+Ke- (t≥0) 利用电容电压的初始值uc(0)=2V和电感电流的初始值 i(0)=1A得到以下两个方程: uc(0)=K1+K2=2 K=6 @1=2,-4K=0=4一 dt K24 最后得到电容电压的零输入响应为 uc(t)(6e 2-4e-)V (t≥0)
将固有频率s 1 =-2和s 2 =-4代入式(9-5)得到 ( ) e e ( 0) 4 2 2 C 1 u t K K t t t 利用电容电压的初始值uC (0)=2V和电感电流的初始值 iL (0)=1A得到以下两个方程: 4 (0) 2 4 d d ( ) (0) 2 L 0 1 2 C C 1 2 C i K K t u t u K K t K1 =6 K2 =-4 ( ) (6e 4e )V ( 0) 2 4 C u t t t t 最后得到电容电压的零输入响应为
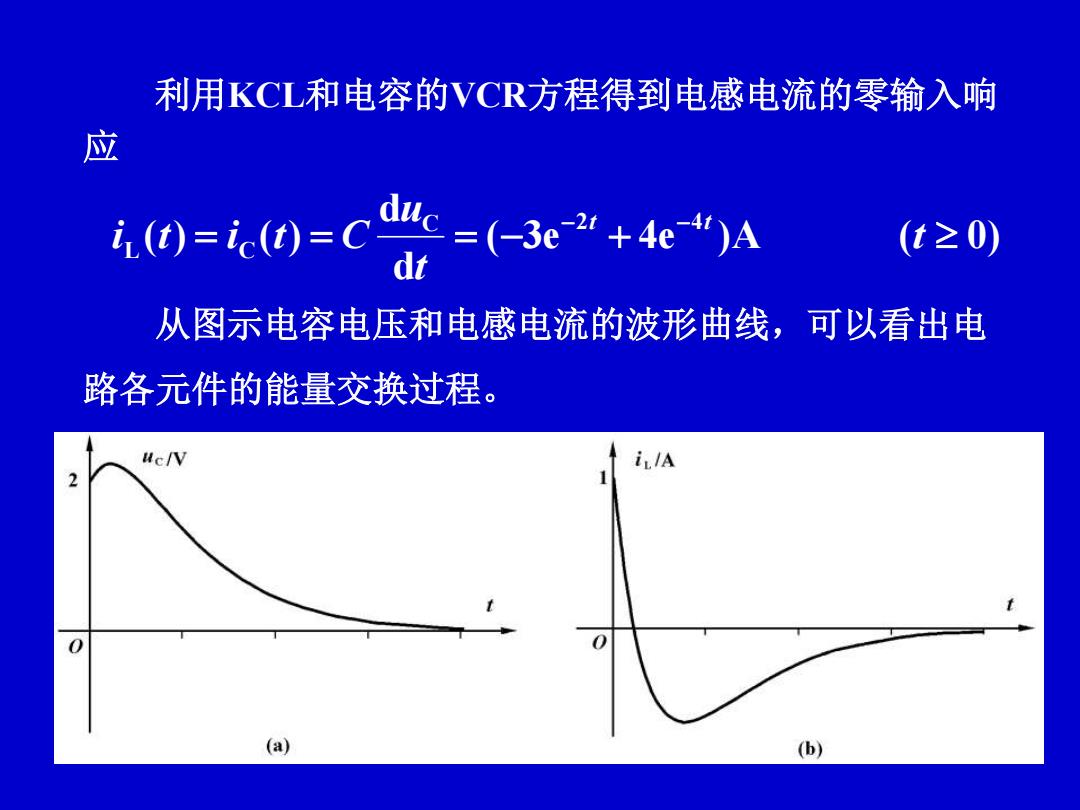
利用KCL和电容的VCR方程得到电感电流的零输入响 应 i (t)=ic(t)=C e=(-3e-2”+4e")A (t≥0) dt 从图示电容电压和电感电流的波形曲线,可以看出电 路各元件的能量交换过程。 uc/V i/A 2 0 (a) (b)
利用KCL和电容的VCR方程得到电感电流的零输入响 应 ( 3e 4e )A ( 0) d d ( ) ( ) C 2 4 L C t t u i t i t C t t 从图示电容电压和电感电流的波形曲线,可以看出电 路各元件的能量交换过程
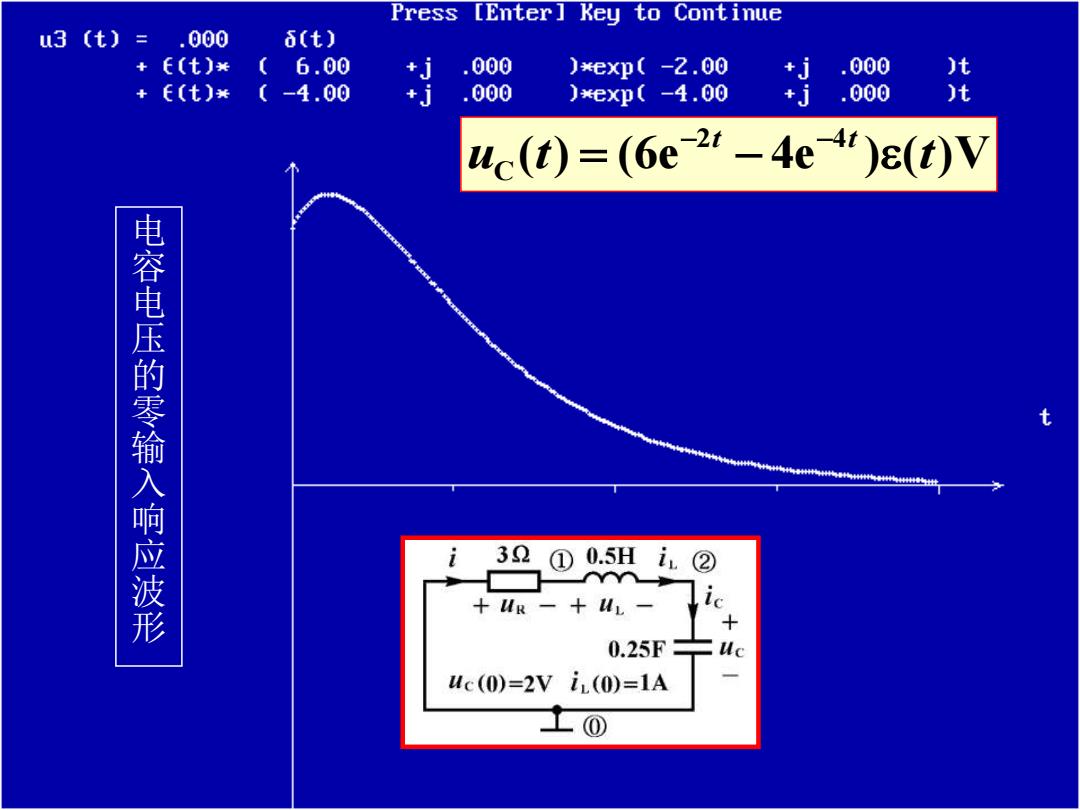
Press [Enter]Key to Continue u3(t)=.000 (t) +E(t)¥ (6.00 +j .000 )exp(-2.00 +j .000 )t +E〔t)* (-4.00 +j .000 )exp(-4.00 +j.000 )t 4c(t)=(6e21-4e4r)ε(t)V 电容电压的零输入响应波形 i 32 ① 0.5H i② +R-+ 4L- ic + 0.25F= Mc(0)=2ViL(0)=1A
( ) ( 6 e 4 e ) ( ) V 2 4 C u t t t t 电容电压的零输入响应波形