
第八章一阶电路分析 由一阶微分方程描述的电路称为一阶电路。本章主要 讨论由直流电源驱动的含一个动态元件的线性一阶电路。 含一个电感或一个电容加上一些电阻元件和独立电源组成 的线性一阶电路,可以将连接到电容或电感的线性电阻单 口网络用戴维宁-诺顿等效电路来代替(如图8-1和8-2 所示)。 (b) (a) (b) 图8-1 图8-2
第八章 一阶电路分析 由一阶微分方程描述的电路称为一阶电路。本章主要 讨论由直流电源驱动的含一个动态元件的线性一阶电路。 含一个电感或一个电容加上一些电阻元件和独立电源组成 的线性一阶电路,可以将连接到电容或电感的线性电阻单 口网络用戴维宁-诺顿等效电路来代替(如图8-1和8-2 所示)。 图8-1 图8-2
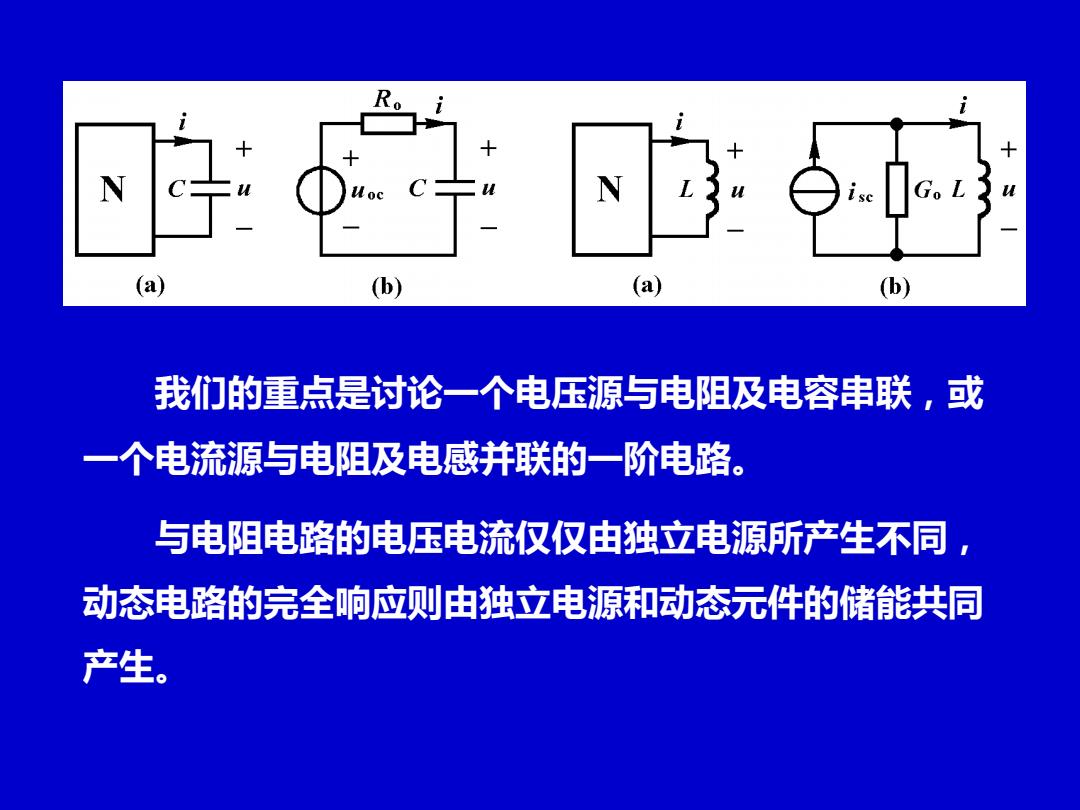
(a) (b) (a) (b) 我们的重点是讨论一个电压源与电阻及电容串联,或 一个电流源与电阻及电感并联的一阶电路。 与电阻电路的电压电流仅仅由独立电源所产生不同, 动态电路的完全响应则由独立电源和动态元件的储能共同 产生
我们的重点是讨论一个电压源与电阻及电容串联,或 一个电流源与电阻及电感并联的一阶电路。 与电阻电路的电压电流仅仅由独立电源所产生不同, 动态电路的完全响应则由独立电源和动态元件的储能共同 产生

仅由动态元件初始条件引起的响应称为零输入响应。 仅由独立电源躬引起的响应称为零状态响应。 动态电路分析的基本方法是建立微分方程,然后用数 学方法求解微分方程,得到电压电流响应的表达式
仅由动态元件初始条件引起的响应称为零输入响应。 仅由独立电源引起的响应称为零状态响应。 动态电路分析的基本方法是建立微分方程,然后用数 学方法求解微分方程,得到电压电流响应的表达式
§8-1零输入响应 一、 RC电路的零输入响应 图8-3(a)所示电路中的开关原来连接在1端,电压源U。 通过电阻R对电容充电,假设在开关转换以前,电容电压 已经达到U。在0时开关迅速由1端转换到2端。 已经充电 的电容脱离电压源而与电阻并联,如图(b)所示。 >0 (a) (b) 图8-3
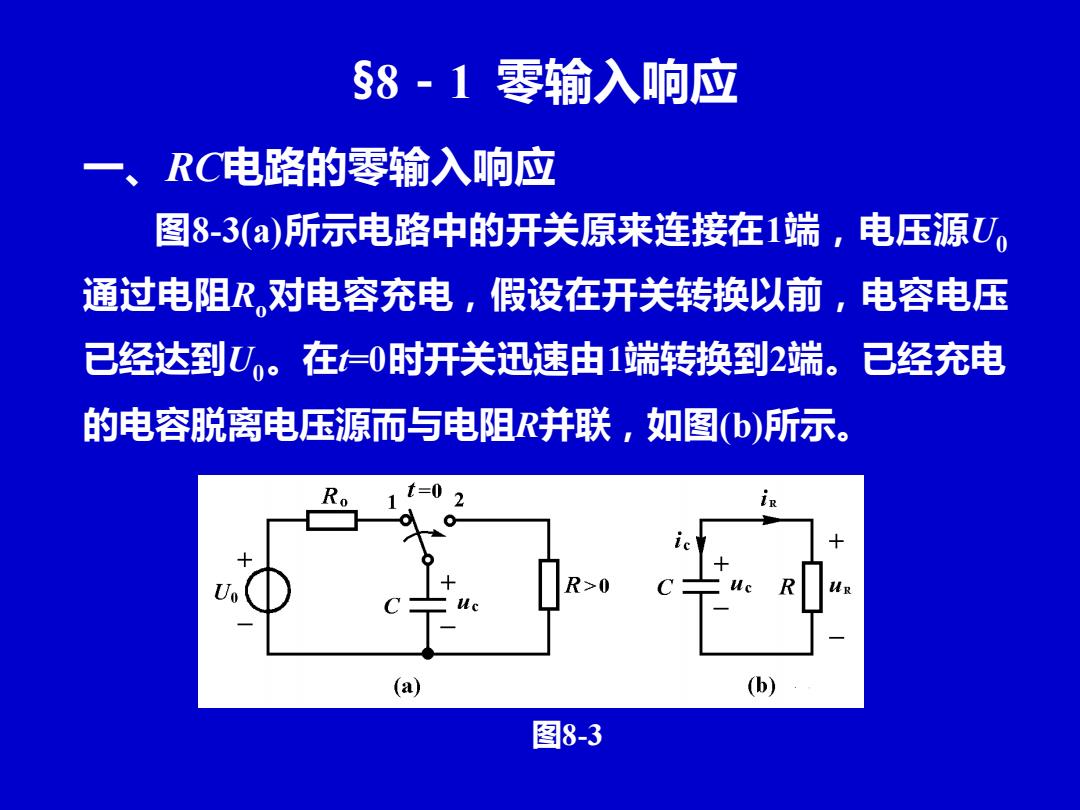
§8-1 零输入响应 图8-3(a)所示电路中的开关原来连接在1端,电压源U0 通过电阻Ro对电容充电,假设在开关转换以前,电容电压 已经达到U0。在t=0时开关迅速由1端转换到2端。已经充电 的电容脱离电压源而与电阻R并联,如图(b)所示。 图8-3 一、RC电路的零输入响应
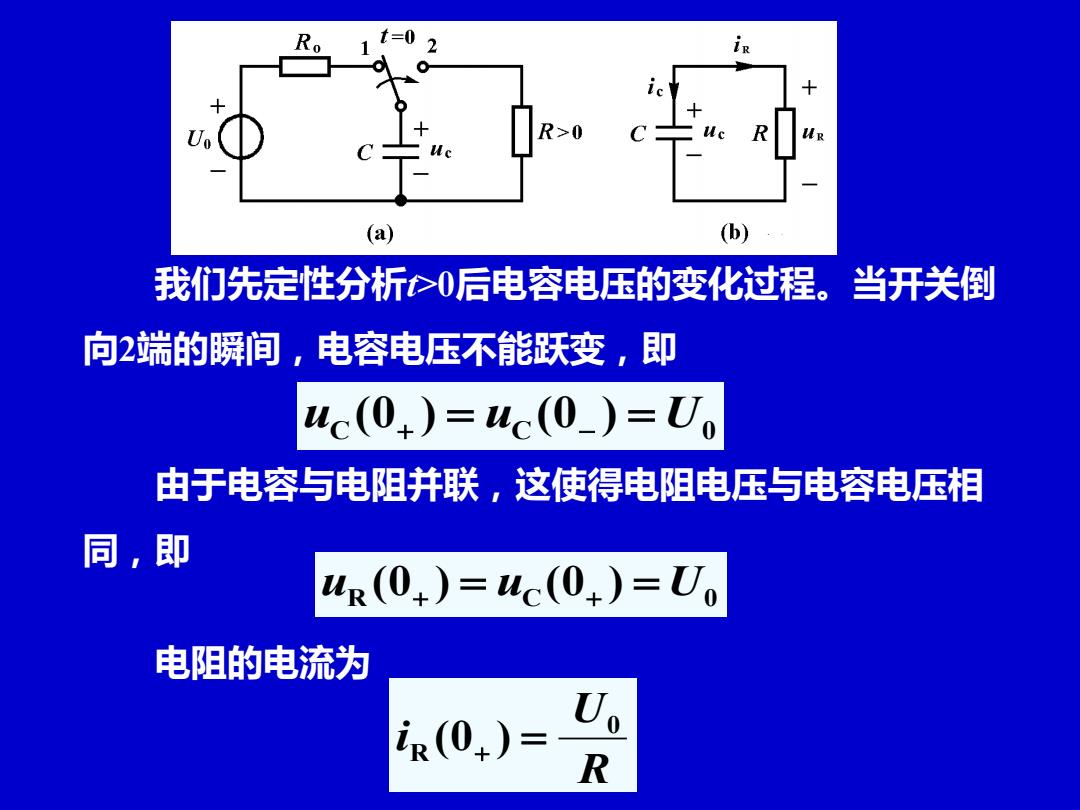
in (a) (b) 我们先定性分析>0后电容电压的变化过程。当开关倒 向2端的瞬间,电容电压不能跃变,即 4c(0+)=uc(0_)=Uo 由于电容与电阻并联,这使得电阻电压与电容电压相 同,即 uk(0+)=u(0+)=Uo 电阻的电流为 iR(0+)= R
我们先定性分析t>0后电容电压的变化过程。当开关倒 向2端的瞬间,电容电压不能跃变,即 C C 0 u (0+ ) = u (0− ) = U 由于电容与电阻并联,这使得电阻电压与电容电压相 同,即 R C 0 u (0+ ) = u (0+ ) = U 电阻的电流为 R U i 0 R (0+ ) =

该电流在电阻中引起的功率和能量为 p(t)=R项(t) W(FRR(传)d5 电容中的能量为 -C 随着时间的增长,电阻消耗的能量需要电容来提供 这造成电容电压的下降。一直到电容上电压变为零和电容 放出全部存储的能量为止。也就是电容电压从初始值 4c0)=U逐渐减小到零的变化过程。这一过程变化的快慢 取决于电阻消耗能量的速率
该电流在电阻中引起的功率和能量为 = t p t Ri t W t R i d 0 2 R R 2 R ( ) ( ) ( )= ( ) 电容中的能量为 随着时间的增长,电阻消耗的能量需要电容来提供, 这造成电容电压的下降。一直到电容上电压变为零和电容 放出全部存储的能量为止。也就是电容电压从初始值 uC (0+ )=U0逐渐减小到零的变化过程。这一过程变化的快慢 取决于电阻消耗能量的速率。 ( ) 2 1 ( ) 2 C C W t = Cu t
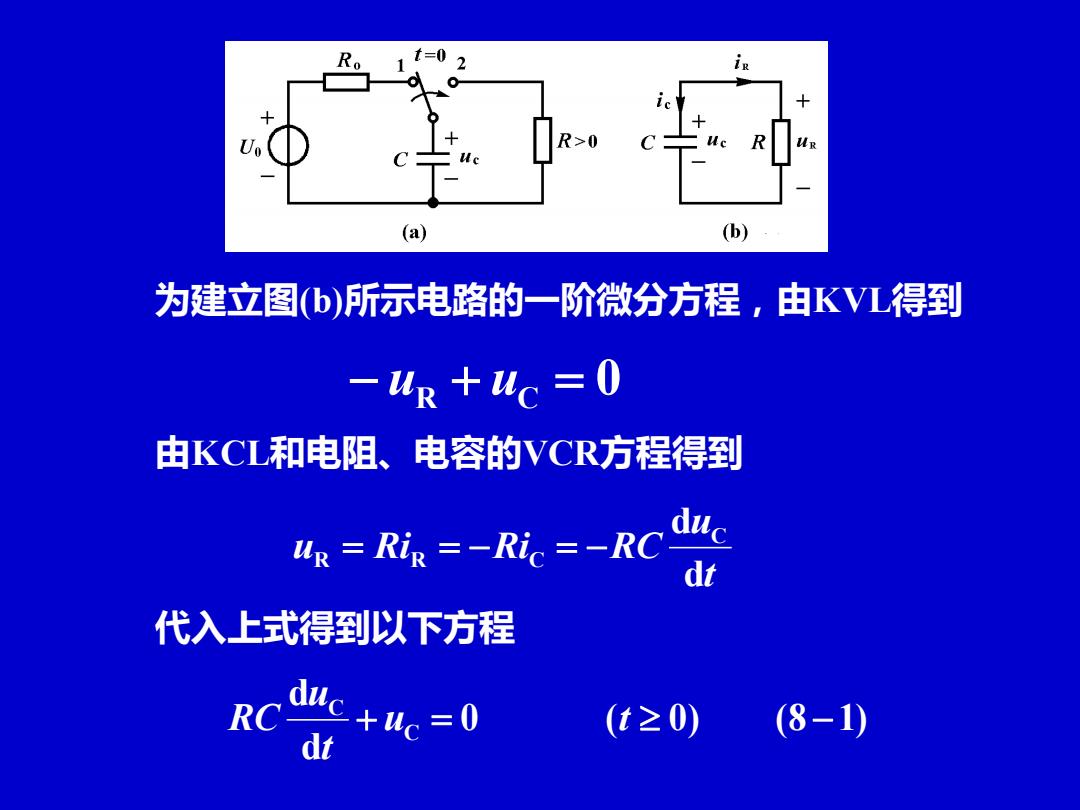
in (a) (b) 为建立图(b)所示电路的一阶微分方程,由KVL得到 -ur uc 0 由KCL和电阻、电容的VCR方程得到 4m=R=-R=-RC d 代入上式得到以下方程 Rc+=0 (t≥0) (8-1) dt
为建立图(b)所示电路的一阶微分方程,由KVL得到 0 − uR + uC = 由KCL和电阻、电容的VCR方程得到 t u u Ri Ri RC d d C R = R = − C = − 代入上式得到以下方程 0 ( 0) (8 1) d d C C + u = t − t u RC
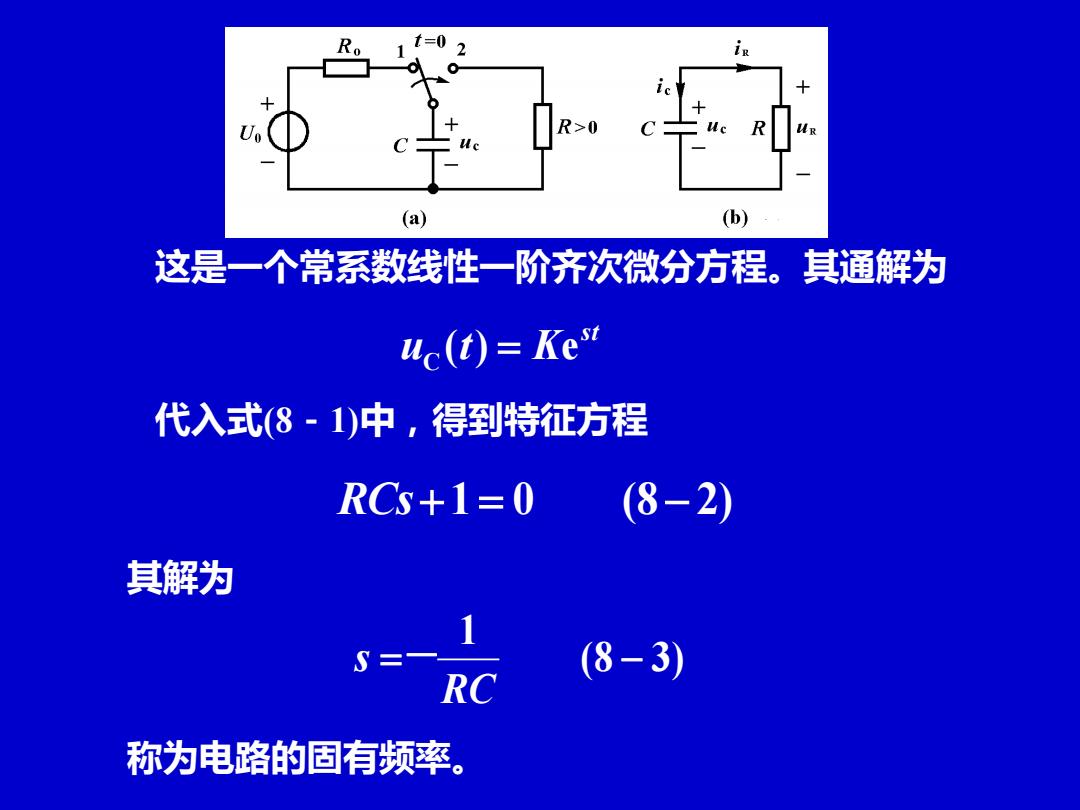
\B7 (a) (b) 这是一个常系数线性一阶齐次微分方程。其通解为 uc(t)=Kex 代入式(8-1)中,得到特征方程 RC+1=0 (8-2) 其解为 S三一 (8-3) RC 称为电路的固有频率
这是一个常系数线性一阶齐次微分方程。其通解为 st u (t) Ke C = 代入式(8-1)中,得到特征方程 RCs+1 = 0 (8− 2) 其解为 (8 3) 1 = − RC s - 称为电路的固有频率

于是电容电压变为 uc(t)=Ke RC t≥0 式中K是一个常量,由初始条件确定。当=0时上式变 为 uc(0.)=Ke RC =K 根据初始条件 uc(0+)=uc(0_)=U 求得 K=U
于是电容电压变为 ( ) e t 0 C = − RC t u t K 式中K是一个常量,由初始条件确定。当t=0+时上式变 为 u K K RC t = = − + (0 ) e C 根据初始条件 C C 0 u (0+ ) = u (0− ) = U 求得 K = U0
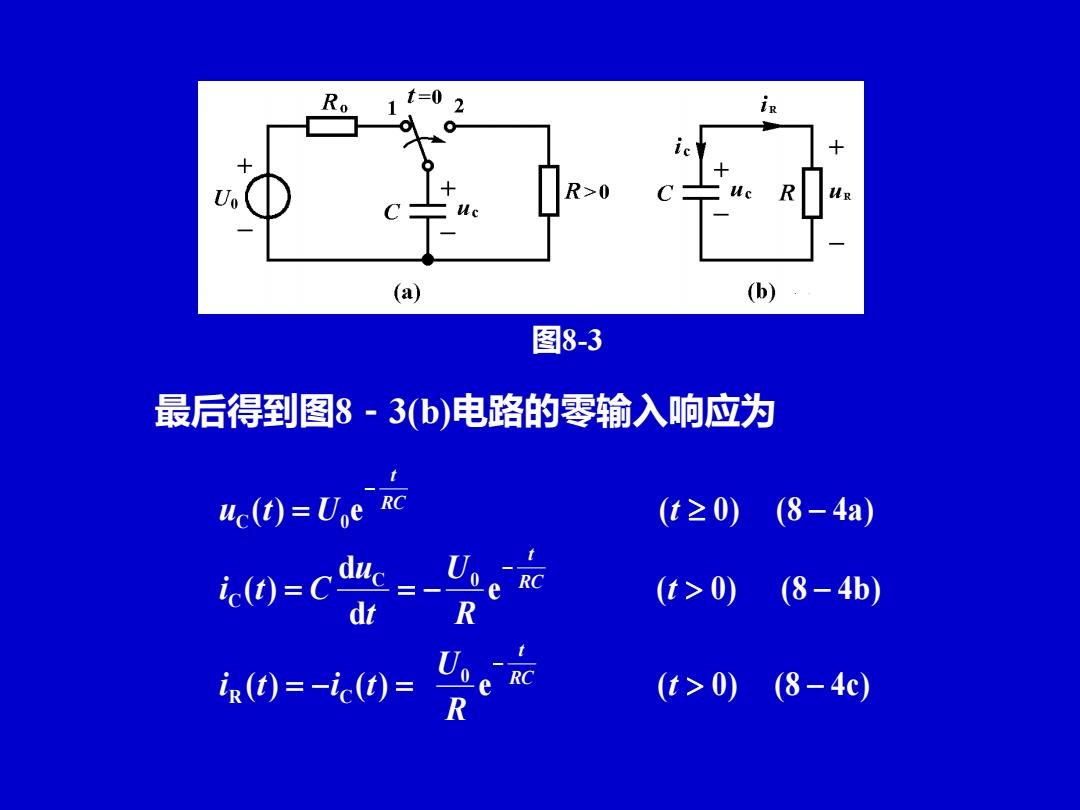
in ic (a) (b) 图8-3 最后得到图8-3b)电路的零输入响应为 uc(t)=Ue rc (t≥0) (8-4a) 40=c此e-乐c安 (t>0)(8-4b) dt k0=-=费女 (t>0)(8-4c)
( ) ( ) e ( 0) (8 4c) e ( 0) (8 4b) d d ( ) ( ) e ( 0) (8 4a) 0 R C C 0 C C 0 = − = − = = − − = − − − − t R U i t i t t R U t u i t C u t U t RC t RC t RC t 最后得到图8-3(b)电路的零输入响应为 图8-3