
明 肥市第五中学 Hefei No.5 Senior High School 理驾学 第七章随机变量及 其分布 善行健美 7.3.1离散型随机变量的均值
7.3.1离散型随机变量的均值 第七章 随机变量及 其分布

对于离散型随机变量,可以由它的概率分布列确定与该随机变 量相关事件的概率。但在实际问题中,有时我们更感兴趣的是随机 变量的某些数字特征。例如,要了解某班同学在一次数学测验中的 总体水平,很重要的是看平均分;要了解某班同学数学成绩是否 “两极分化”则需要考察这个班数学成绩的方差。 我们还常常希望直接通过数字来反映随机变量的某个方面的特征, 最常用的有期望与方差
问题导学 对于离散型随机变量,可以由它的概率分布列确定与该随机变 量相关事件的概率。但在实际问题中,有时我们更感兴趣的是随机 变量的某些数字特征。例如,要了解某班同学在一次数学测验中的 总体水平,很重要的是看平均分;要了解某班同学数学成绩是否 “两极分化”则需要考察这个班数学成绩的方差。 我们还常常希望直接通过数字来反映随机变量的某个方面的特征, 最常用的有期望与方差
探究1.甲乙两名射箭运动员射中目标靶的环数的分布列如下表所示: 环数X 7 8 9 10 甲射中的概率 0.1 0.2 0.3 0.4 乙射中的概率 0.15 0.25 0.4 0.2 如何比较他们射箭水平的高低呢? 类似两组数据的比较,首先比较击中的平均环数如果平均环数相等,再看稳定性.假设甲 m n2 n3 ns 射箭n次,射中7环、8环、9环和10环的频率分别为:n’n’n’n 甲n次射箭射中的平均环数 x=7x+8×+9x+10x24 n n n
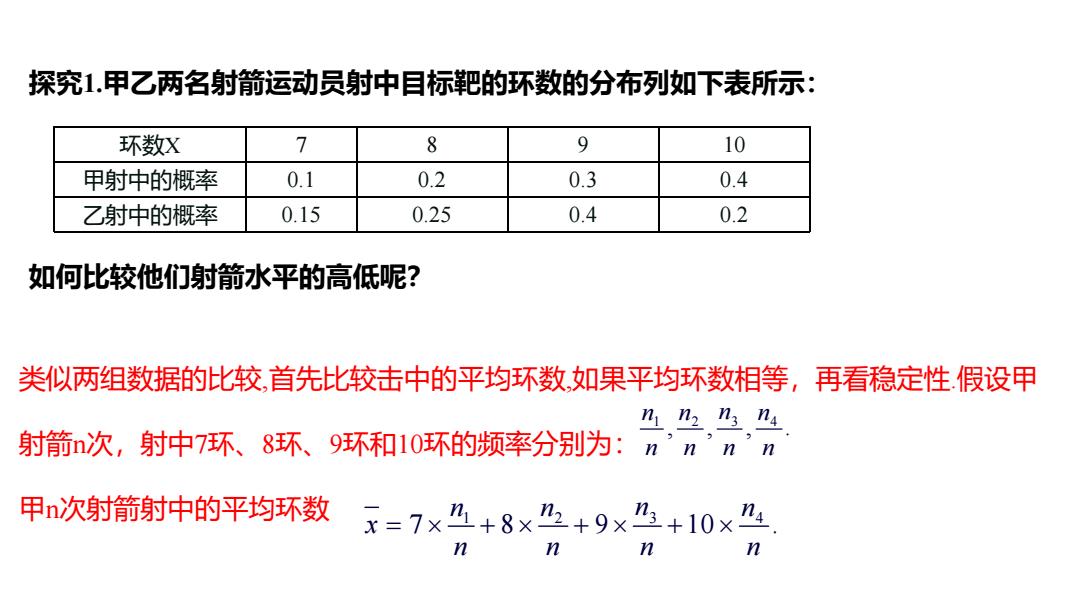
探究1.甲乙两名射箭运动员射中目标靶的环数的分布列如下表所示: 如何比较他们射箭水平的高低呢? 环数X 7 8 9 10 甲射中的概率 0.1 0.2 0.3 0.4 乙射中的概率 0.15 0.25 0.4 0.2 类似两组数据的比较,首先比较击中的平均环数,如果平均环数相等,再看稳定性.假设甲 射箭n次,射中7环、8环、9环和10环的频率分别为: 甲n次射箭射中的平均环数 1 2 3 4 , , , . n n n n n n n n 1 2 3 4 7 8 9 10 . n n n n x n n n n 问题探究

当n足够大时,频率稳定于概率,所以x稳定于7×0.1+8×0.2+9×0.3+10×0.4=9 即甲射中平均环数的稳定值(理论平均值)为9, 这个平均值的大小可以反映甲运动员的射箭水平 同理,乙射中环数的平均值为7×0.15+8×0.25+9×0.4+10×0.2=8.65 从平均值的角度比较,甲的射箭水平比乙高
当n足够大时,频率稳定于概率,所以x稳定于7×0.1+8×0.2+9×0.3+10×0.4=9. 即甲射中平均环数的稳定值(理论平均值)为9, 这个平均值的大小可以反映甲运动员的射箭水平. 同理,乙射中环数的平均值为7×0.15+8×0.25+9×0.4+10×0.2=8.65. 从平均值的角度比较,甲的射箭水平比乙高

一、离散型随机变量取值的平均值. 一般地,若离散型随机变量X的概率分布为: X X1 X2 Xi Xn P P2 Pi Pn 则称E(X)=x1p1+x2p2+…+xp:++xnPn 为随机变量X的均值(mean)或数学期望(mathematical expectation),数学期望简称期 望.均值是随机变量可能取值关于取值概率的加权平均数,它综合了随机变量的取值和 取值的概率,反映了随机变量取值的平均水平
一、离散型随机变量取值的平均值. 一般地,若离散型随机变量X的概率分布为: 为随机变量X的均值(mean)或数学期望(mathematical expectation),数学期望简称期 望.均值是随机变量可能取值关于取值概率的加权平均数,它综合了随机变量的取值和 取值的概率,反映了随机变量取值的平均水平. X x1 x2 … xi … xn P p1 p2 … pi … pn 概念解析

例1.在篮球比赛中,罚球命中1次得1分,不中得0分如果某运动员罚球命中的概率为0.8, 那么他罚球1次的得分的均值是多少? 分析:罚球有命中和不中两种可能结果,命中时X=1,不中时X0,因此随机变量X服从 两点分布,X的均值反映了该运动员罚球1次的平均得分水平 解:因为PX=1)=0.8,P(X=0)=0.2, 所以E(X=1×P(X=1)+0×P(X=0)=1×0.8+0×0.2=0.8 即该运动员罚球1次的得分X的均值是0.8
例1. 在篮球比赛中,罚球命中1次得1分,不中得0分,如果某运动员罚球命中的概率为0.8, 那么他罚球1次的得分X的均值是多少? 分析:罚球有命中和不中两种可能结果,命中时X=1,不中时X=0,因此随机变量X服从 两点分布,X的均值反映了该运动员罚球1次的平均得分水平. 解:因为P(X=1)=0.8,P(X=0)=0.2, 所以E(X)=1×P(X=1)+0×P(X=0)=1×0.8+0×0.2 =0.8 即该运动员罚球1次的得分X的均值是0.8. 典例解析

一般地,如果随机变量X服从两点分布, 那么:E(X)=1×p+0×(1-P)=p. X 1 0 P p 1-p
X 1 0 P p 1-p 概念解析

例2抛掷一枚质地均匀的骰子,设出现的点数为X,求X的均值 分析:先求出X的分布列,再根据定义计算X的均值。 解:X的分布列为P(X=k)=,k=1,2,3,4,5,6 因此,E(X)=(1+2+3+4+5+6)=3.5
例2.抛掷一枚质地均匀的骰子,设出现的点数为X,求X的均值. 分析:先求出X的分布列,再根据定义计算X的均值。 典例解析

求离散型随机变量的均值的步骤: (1)理解X的实际意义,写出X全部可能取值; (2)求出X取每个值时的慨率: (3)写出X的分布列(有时也可省略): (4)利用定义公式E(X)=1xP,求出均值
归纳总结

跟踪训练1某地最近出台一项机动车驾照考试规定:每位考试者一 年之内最多有4次参加考试的机会,一旦某次考试通过,即可领取驾照, 不再参加以后的考试,否则就一直考到第4次为止.如果李明决定参加驾 照考试,设他每次参加考试通过的概率依次为0.6,0.7,0.8,0.9,求在一年 内李明参加驾照考试次数X的分布列和的均值
跟踪训练 跟踪训练1.某地最近出台一项机动车驾照考试规定:每位考试者一 年之内最多有4次参加考试的机会,一旦某次考试通过,即可领取驾照, 不再参加以后的考试,否则就一直考到第4次为止.如果李明决定参加驾 照考试,设他每次参加考试通过的概率依次为0.6,0.7,0.8,0.9,求在一年 内李明参加驾照考试次数X的分布列和X的均值.