
5.1.1变化率问题导学案 【学习目标】 1.通过求高台跳水运动员在具体时刻的瞬时速度,体会求瞬时速度的一般方法 2通过求曲线处某点处切线斜率的过程,体会求切线斜率的一般方法 3.理解函数的平均变化率,瞬时变化率的概念。 【学习重难点】 重点:理解瞬时速度和曲线上某点处切线斜率的概念及算法 难点:理解函数的平均变化率,瞬时变化率的概念 【学习过程】 1.平均变化率 对于函数y=∫x),从x到x2的平均变化率: (1)自变量的改变量:△x=」 (2)函数值的改变量:△y= ()平均变化率是 2瞬时速度与瞬时变化率 (1)物体在 的速度称为瞬时速度, (2)函数f(x)在x=和处的瞬时变化率是函数f(x)从o到0十△x的平均变化率在△x→0时的极限, y 即lim△x △x-→0 3.曲线的切线斜率 (仙)设Po,∫o》,P心,f)是曲线y=寸)上任意不同两点,则平均变化率x二。 x-X0 fx十△x二0一为割线PoP的一 △x (2)当P点逐渐靠近Po点,即△x逐渐变小,当△x→0时,瞬时变化率 就是y =f(x)在xo处的的斜率即k= 问题1高台跳水运动员的速度 高台跳水运动中,运动员在运动过程中的重心相对于水面的高度(单位:)与起跳后的时间(单 位:S)存在函数关系 h(0=-4.91+4.81+11 如何描述用运动员从起跳到入水的过程中运动的快慢程度呢?
5.1.1 变化率问题 导学案 【学习目标】 1. 通过求高台跳水运动员在具体时刻的瞬时速度,体会求瞬时速度的一般方法. 2.通过求曲线处某点处切线斜率的过程,体会求切线斜率的一般方法. 3.理解函数的平均变化率,瞬时变化率的概念. 【学习重难点】 重点:理解瞬时速度和曲线上某点处切线斜率的概念及算法 难点:理解函数的平均变化率,瞬时变化率的概念 【学习过程】 1.平均变化率 对于函数 y=f (x),从 x1到 x2的平均变化率: (1)自变量的改变量:Δx=_______. (2)函数值的改变量:Δy=_____________. (3)平均变化率Δy Δx = = . 2.瞬时速度与瞬时变化率 (1)物体在________的速度称为瞬时速度. (2)函数 f (x)在 x=x0处的瞬时变化率是函数 f (x)从 x0到 x0+Δx 的平均变化率在 Δx→0 时的极限, 即 lim Δx→0 Δy Δx = . 3.曲线的切线斜率 (1)设 P0(x0,f (x0)),P(x,f (x))是曲线 y=f (x)上任意不同两点,则平均变化率f x -f x0 x-x0 = f x0+Δx -f x0 Δx 为割线 P0P 的_____. (2)当 P 点逐渐靠近 P0 点,即 Δx 逐渐变小,当 Δx→0 时,瞬时变化率 就是 y =f (x)在 x0处的____的斜率即 k= . 问题 1 高台跳水运动员的速度 高台跳水运动中,运动员在运动过程中的重心相对于水面的高度 h(单位:m)与起跳后的时间 t(单 位:s)存在函数关系 h(t)=-4.9t 2 +4.8t+11. 如何描述用运动员从起跳到入水的过程中运动的快慢程度呢?

直觉告诉我们,运动员从起跳到入水的过程中,在上升阶段运动的越来越慢,在下降阶段运动 的越来越快,我们可以把整个运动时间段分成许多小段,用运动员在每段时间内的平均速度近似的 描述它的运动状态。 例如,在0≤t0时,在时间段[1,1+△]内 。_A)-h1+ h(1+△)-h(1) 1-(1+△r) (1+△r)-1 -49(△)+5△L -4.9(a)1-5△4 -△r △ =-4.9△-5 =-4.9△-5 当△0时,在时间段E1,1十△]内 -0.01 T4.051 0.O1 -5.049 -0.001 -4.9951 0.001 -5.0049 -0.0001 -4.99951 0.0001 -5.0004 -0.00001 一4.999951 o.000 01 一5U0049 -0.000001 -4.9999951 0.000001 -5.0000049 问题2.抛物线的切线的斜率 我们知道,如果一条直线与一个圆只有一个公共点,那么这条直线与这个圆相切,对于一 般的曲线C,如何确定它的切线呢?下面我们以抛物线f(x)=x2为例进行研究 探究3.你认为应该如何定义抛物线f(x)=x2在点Po(1,1)处的切线? 与研究瞬时速度类似为了研究抛物线f(x)=x2在点Po(1,1)处的切线,我们通常在点Po(1,1)的附近 取一点P(x,x2),考察抛物线f(x)=x2的割线P。P的变化情况
直觉告诉我们,运动员从起跳到入水的过程中,在上升阶段运动的越来越慢,在下降阶段运动 的越来越快,我们可以把整个运动时间段分成许多小段,用运动员在每段时间内的平均速度 ̅近似的 描述它的运动状态。 例如,在 0 ≤ t ≤0.5 这段时间里, ̅ ( ) ( ) ( ) 在 1≤ t ≤2 这段时间里, ̅ ( ) ( ) ( ) 一般地,在 ≤ t ≤ 这段时间里, ̅ ( ) ( ) ( ) 探究 1: 计算运动员在 0 ≤ t ≤ 这段时间内的平均速度你发现了什么?你认为用平均速度描述运动 员的运动状态有什么问题吗? 为了精确刻画运动员的运动状态,需要引入瞬时速度的概念。 我们把物体在某一时刻的速度称为瞬时速度。 探究 2:瞬时速度与平均速度有什么关系?你能利用这种关系求运动员在 t=1 是的瞬时速度吗? 问题 2. 抛物线的切线的斜率 我们知道,如果一条直线与一个圆只有一个公共点,那么这条直线与这个圆相切,对于一 般的曲线 C,如何确定它的切线呢?下面我们以抛物线 ( ) 为例进行研究. 探究 3. 你认为应该如何定义抛物线 ( ) 在点 ( )处的切线? 与研究瞬时速度类似为了研究抛物线 ( ) 在点 ( )处的切线,我们通常在点 ( )的附近 取一点 ( ),考察抛物线 ( ) 的割线 的变化情况
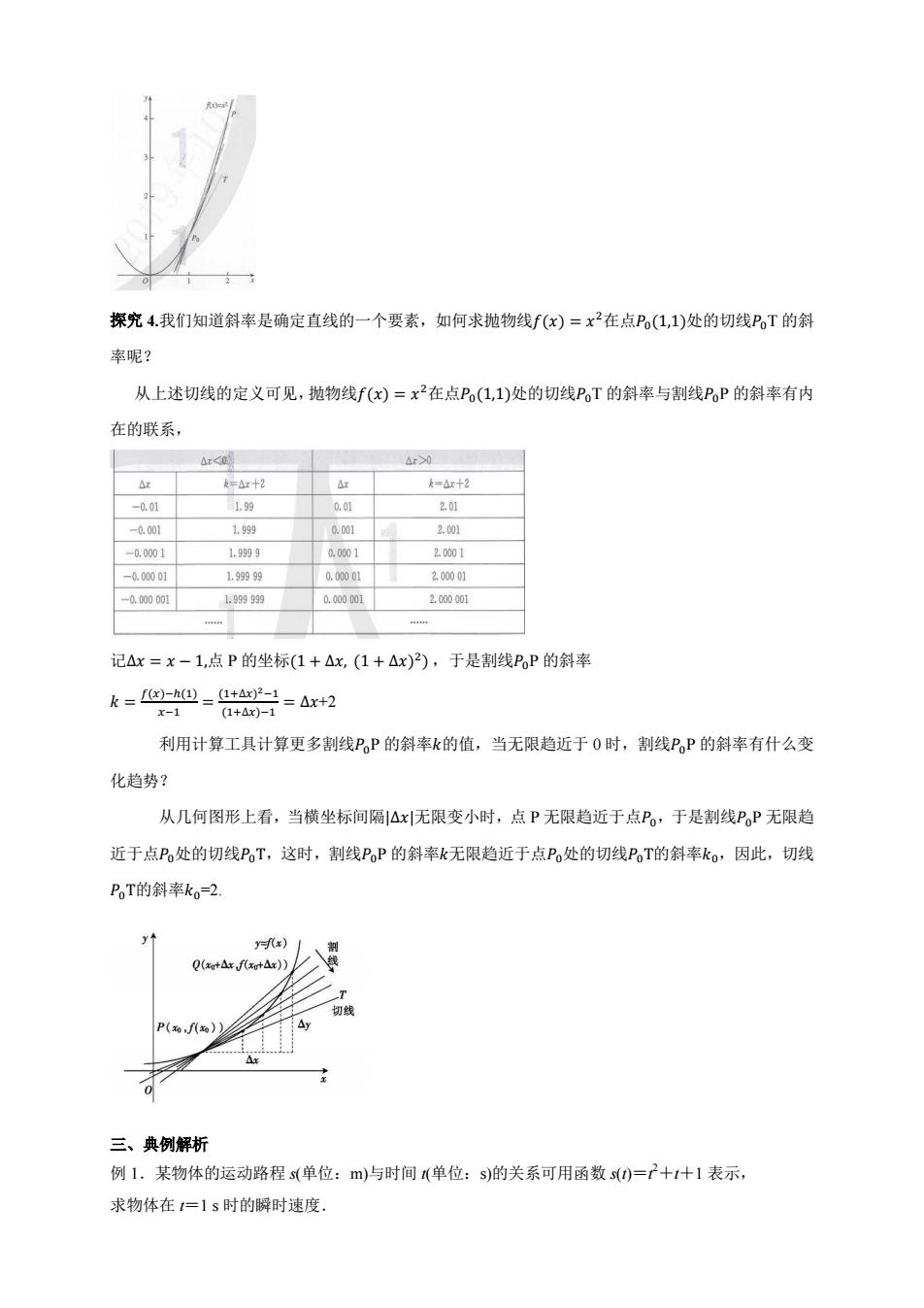
探究4.我们知道斜率是确定直线的一个要素,如何求抛物线f(x)=x2在点P(1,1)处的切线PoT的斜 率呢? 从上述切线的定义可见,抛物线f(x)=x2在点Po(1,1)处的切线PT的斜率与割线PP的斜率有内 在的联系, △r0 △x k=△x十2 k=△x+2 -0.01 1.99 0.01 201 -0.001 1.999 0.001 2.001 -0,0001 1.9999 0.0001 2.D801 -0.00001 1.99999 0.00001 2.00001 -0.000001 1.999999 0.000001 2.000001 444 4444 记△x=x-1,点P的坐标(1+△x,(1+△x)2),于是割线PP的斜率 k=f)-h@=L+a2- =△x+2 x-1 (1+Ax)-1 利用计算工具计算更多割线PP的斜率k的值,当无限趋近于0时,割线PP的斜率有什么变 化趋势? 从几何图形上看,当横坐标间隔△x无限变小时,点P无限趋近于点P。,于是割线PP无限趋 近于点Po处的切线PT,这时,割线PP的斜率k无限趋近于点Po处的切线PT的斜率ko,因此,切线 PT的斜率ko=2. y y=f(x) Q(xot△xf(xot△x)) 切线 三、典例解析 例1.某物体的运动路程s(单位:m)与时间(单位:s)的关系可用函数s()=+1+1表示, 求物体在1=1s时的瞬时速度
探究 4.我们知道斜率是确定直线的一个要素,如何求抛物线 ( ) 在点 ( )处的切线 T 的斜 率呢? 从上述切线的定义可见,抛物线 ( ) 在点 ( )处的切线 T 的斜率与割线 P 的斜率有内 在的联系, 记 点 P 的坐标( ( ) ) ,于是割线 P 的斜率 ( ) ( ) ( ) ( ) +2 利用计算工具计算更多割线 P 的斜率 的值,当无限趋近于 0 时,割线 P 的斜率有什么变 化趋势? 从几何图形上看,当横坐标间隔| |无限变小时,点 P 无限趋近于点 ,于是割线 P 无限趋 近于点 处的切线 ,这时,割线 P 的斜率 无限趋近于点 处的切线 的斜率 ,因此,切线 的斜率 =2. 三、典例解析 例 1.某物体的运动路程 s(单位:m)与时间 t(单位:s)的关系可用函数 s(t)=t 2+t+1 表示, 求物体在 t=1 s 时的瞬时速度.

求运动物体瞬时速度的三个步骤 设非匀速直线运动中物体的位移随时间变化的函数为s=s(1),则求物体在1=0时刻的 瞬时速度的步骤如下: 1写出时间改变量△1,位移改变量△s△=s(t十△t)一s(t), 2求平均速度:下- 3求瞬时速度:当△10时,总”常数 跟踪训练1.在本例条件不变的前提下,试求物体的初速度. 跟踪训练2.在本例条件不变的前提下,试问物体在哪一时刻的瞬时速度为9/s. 例2.己知函数y=x一 则该函数在点x=1处的切线斜率为? 当堂检测 1.物体自由落体的运动方程为s0=这,g=98mS2,若=1m:1+yS1=98s, △1 △1→0 那么下列说法中正确的是() A.9.8m/s是物体从0s到1s这段时间内的速率 B.9.8m/s是1s到(1+△1)s这段时间内的速率 C.9.8ms是物体在1=1s这一时刻的速率 D.9.8m/s是物体从1s到(1+△1)s这段时间内的平均速率 2.已知函数f)=2-1的图象上一点1,1)及其附近一点(1+A,/1+△x,则哈是等于 3.已知函数f(x)=3x+5,求f(x): (1)从0.1到0.2的平均变化率: (2)在区间xo,xo十△x]上的平均变化率. 4.求函数y=在x=2处的切线的斜率
求运动物体瞬时速度的三个步骤 设非匀速直线运动中物体的位移随时间变化的函数为 s=s(t) ,则求物体在 t=t0 时刻的 瞬时速度的步骤如下: 1 写出时间改变量 Δt,位移改变量 Δs Δs=s(t0+Δt) -s(t0 ) . 2 求平均速度: v = Δs Δt . 3 求瞬时速度 v:当 Δt→0 时,Δs Δt →v 常数 . 跟踪训练 1.在本例条件不变的前提下,试求物体的初速度. 跟踪训练 2.在本例条件不变的前提下,试问物体在哪一时刻的瞬时速度为 9 m/s. 例 2.已知函数 y=x- 1 x ,则该函数在点 x=1 处的切线斜率为? 当堂检测 1.物体自由落体的运动方程为 s(t)= 1 2 gt2,g=9.8 m/s2,若 v=lim Δt→0 s 1+Δt -s 1 Δt =9.8 m/s, 那么下列说法中正确的是( ) A.9.8 m/s 是物体从 0 s 到 1 s 这段时间内的速率 B.9.8 m/s 是 1 s 到(1+Δt)s 这段时间内的速率 C.9.8 m/s 是物体在 t=1 s 这一时刻的速率 D.9.8 m/s 是物体从 1 s 到(1+Δt)s 这段时间内的平均速率 2.已知函数 f (x)=2x 2-1 的图象上一点(1,1)及其附近一点(1+Δx,f (1+Δx)),则Δy Δx 等于________. 3.已知函数 f (x)=3x 2+5,求 f (x): (1)从 0.1 到 0.2 的平均变化率; (2)在区间[x0,x0+Δx]上的平均变化率. 4.求函数 y= 4 x 2在 x=2 处的切线的斜率.