志鸿优化系列丛书 志鸿优化网,永远提供更新的: 丛书主编任志湖。 http://www.zhyh.org 1.4.2 用空间向量研究距离、夹角问题 第2课时) 用空间向量研究夹角问题 课后·训练提升 基础巩固 1.若直线1的方向向量与平面α的法向量的夹角为150°,则直线1与平面a所成的角为) A.30° B.60° C.150° D.120° 答案B 2在长方体ABCD-4B1CD,中,若AB=2BC=2,DD1是则AC与BD,所成角的余弦值是() A.0 B.30 C.3v而 D而 70 70 70 答案A D 解析如图建立空间直角坐标系,则D0,0 ,B2.0,420,0C0,20所以BD-2-2星,元- 2,2,0) 设AC与BD1所成的角为Q,则cos0=lcos匹C-0 BDACI 3.在正四棱柱ABCD-A1B1CD1中,己知AA1=2AB,则CD与平面BDC所成角的正弦值为) A号 B③ 3 D 答案A 解析不妨设AB-1,则A41=2. 1
1 1.4.2 用空间向量研究距离、夹角问题 第 2 课时 用空间向量研究夹角问题 课后· 基础巩固 1.若直线 l 的方向向量与平面 α 的法向量的夹角为 150°,则直线 l 与平面 α 所成的角为( ) A.30° B.60° C.150° D.120° 答案:B 2.在长方体 ABCD-A1B1C1D1中,若 AB=2,BC=2,DD1= 3 2 ,则 AC 与 BD1 所成角的余弦值是( ) A.0 B. 3√70 70 C.- 3√70 70 D. √70 70 答案:A 解析:如图建立空间直角坐标系,则 D1 0,0,3 2 ,B(2,2,0),A(2,0,0),C(0,2,0),所以𝐵𝐷1 ⃗⃗ ⃗⃗ = -2,-2,3 2 ,𝐴⃗⃗𝐶 =(- 2,2,0). 设 AC 与 BD1 所成的角为 θ,则 cos θ=|cos|=|𝐵𝐷1 ⃗⃗⃗⃗⃗⃗⃗⃗ ·𝐴𝐶⃗⃗⃗⃗ | |𝐵𝐷1 ⃗⃗⃗⃗⃗⃗⃗⃗ ||𝐴𝐶⃗⃗⃗⃗ | =0. 3.在正四棱柱 ABCD-A1B1C1D1中,已知 AA1=2AB,则 CD 与平面 BDC1 所成角的正弦值为( ) A. 2 3 B. √3 3 C. √2 3 D. 1 3 答案:A 解析:不妨设 AB=1,则 AA1=2

志鸿优化系列丛书 志鸿优化网,永远提供更新的: 丛书主编任志河。 http://www.zhyh.org 以D1为原点,D1A1,D1C1,D1D所在直线分别为x轴、y轴、:轴,建立空间直角坐标系,如图所示,则 D0,0,2),C1(0,1,0,B1,1,2),C(0,1,2),所以DB-(1,1,0),DC1=-0,1,-2),DC=(0,1,0) 设n=(x,y,)为平面BDC的法向量, 则nD丽=0、即gty=0取m22, n DC=0, y-2z=0. 设CD与平面BDC1所成的角为O, 则sn0=-Dt=号 4.己知正四棱锥S-ABCD的侧棱长与底面边长相等,E为SB的中点,则AE,SD所成角的余弦值为 () A时 B c 房 客案c 解析不妨设正四棱锥的棱长为2,如图,以正方形ABCD的中心O为原点,建立空间直角坐标系,则 A1,-1,0),D-1-1,0,S0,022是是, 2’22 所以证-(号历1-lV2 2,2,2 设AE,SD所成的角为O, 则cos0=cos1m严= AEISDI 故AE,SD所成角的余弦值为号 5.(多选题)已知P为正方形ABCD所在平面外一点,PA⊥平面ABCD,若PA=AB,则平面PAB与平面 PCD所形成的二面角的大小可以为() A30° B.45° C.135° D.150° 答案BC 解析建立如图所示的空间直角坐标系A 2
2 以 D1 为原点,D1A1,D1C1,D1D 所在直线分别为 x 轴、y 轴、z 轴,建立空间直角坐标系,如图所示,则 D(0,0,2),C1(0,1,0),B(1,1,2),C(0,1,2),所以𝐷𝐵⃗ ⃗ =(1,1,0),𝐷𝐶1 ⃗⃗⃗⃗⃗ =(0,1,-2),𝐷𝐶⃗⃗⃗ =(0,1,0). 设 n=(x,y,z)为平面 BDC1 的法向量, 则{ 𝑛·𝐷𝐵⃗ ⃗ = 0, 𝑛·𝐷𝐶1 ⃗⃗⃗⃗⃗ = 0, 即 { 𝑥 + 𝑦 = 0, 𝑦-2𝑧 = 0, 取 n=(-2,2,1). 设 CD 与平面 BDC1 所成的角为 θ, 则 sin θ=|cos|=|𝐷𝐶⃗⃗⃗⃗⃗ ·𝑛| |𝐷𝐶⃗⃗⃗⃗⃗ ||𝑛| = 2 3 . 4.已知正四棱锥 S-ABCD 的侧棱长与底面边长相等,E 为 SB 的中点,则 AE,SD 所成角的余弦值为 ( ) A. 1 3 B. √2 3 C. √3 3 D. 2 3 答案:C 解析:不妨设正四棱锥的棱长为 2,如图,以正方形 ABCD 的中心 O 为原点,建立空间直角坐标系,则 A(1,-1,0),D(-1,-1,0),S(0,0,√2),E 1 2 , 1 2 , √2 2 , 所以𝐴𝐸⃗⃗⃗ = - 1 2 , 3 2 , √2 2 ,𝑆𝐷⃗⃗ =(-1,-1,-√2). 设 AE,SD 所成的角为 θ, 则 cos θ=|cos|=|𝐴𝐸⃗⃗⃗⃗⃗ ·𝑆𝐷⃗⃗⃗⃗ | |𝐴𝐸⃗⃗⃗⃗⃗ ||𝑆𝐷⃗⃗⃗⃗ | = √3 3 . 故 AE,SD 所成角的余弦值为√3 3 . 5.(多选题)已知 P 为正方形 ABCD 所在平面外一点,PA⊥平面 ABCD,若 PA=AB,则平面 PAB 与平面 PCD 所形成的二面角的大小可以为( ) A.30° B.45° C.135° D.150° 答案:BC 解析:建立如图所示的空间直角坐标系 Axyz

志鸿优化系列丛书 志鸿优化网永远提供更新的! 丛书主编任志湖。 http://www.zhyh.org 1 设PA=AB=1,则A(0,0,0),D0,1,0),P(0,0,1),于是AD=(0,1,0) 取PD的中点E,连接AE, 则o,》 于是正=(02》 易知AD是平面PAB的一个法向量,A正是平面PCD的一个法向量, 0s号 平面PAB与平面PCD所形成的二面角的余弦值为士三 .平面PAB与平面PCD所形成的二面角的大小为45°或135° 6.如图,在正方体ABCD-A1B1CD1中,M为CC的中点,O为底面ABCD的中心,P为A1B上的任意点, 则直线BM与OP所成的角为 D C B B 答案 解析如图,以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系. D 设正方体的棱长为2,A1P=x(0≤x≤2) 则O1,1,0),P(2,x,2),B2,2,0),M0,2,1)2 所以0丽=(1,x-1,2),BM=(-2,0,1). 所以O丽.BM=0,所以丽⊥BM,即OP⊥BM 3
3 设 PA=AB=1,则 A(0,0,0),D(0,1,0),P(0,0,1),于是𝐴𝐷⃗⃗⃗⃗ =(0,1,0). 取 PD 的中点 E,连接 AE, 则 E(0, 1 2 , 1 2 ), 于是𝐴𝐸⃗⃗⃗ = (0, 1 2 , 1 2 ). 易知𝐴𝐷⃗⃗⃗⃗ 是平面 PAB 的一个法向量,𝐴𝐸⃗⃗⃗ 是平面 PCD 的一个法向量, ∵cos= √2 2 , ∴平面 PAB 与平面 PCD 所形成的二面角的余弦值为± √2 2 . ∴平面 PAB 与平面 PCD 所形成的二面角的大小为 45°或 135°. 6.如图,在正方体 ABCD-A1B1C1D1 中,M 为 C1C 的中点,O 为底面 ABCD 的中心,P 为 A1B1 上的任意点, 则直线 BM 与 OP 所成的角为 . 答案: π 2 解析:如图,以 D 为原点,DA,DC,DD1 所在直线分别为 x 轴、y 轴、z 轴,建立空间直角坐标系. 设正方体的棱长为 2,A1P=x(0≤x≤2), 则 O(1,1,0),P(2,x,2),B(2,2,0),M(0,2,1), 所以𝑂𝑃⃗⃗⃗ =(1,x-1,2),𝐵𝑀⃗⃗⃗⃗ =(-2,0,1). 所以𝑂𝑃⃗⃗⃗ · 𝐵𝑀⃗⃗⃗⃗ =0,所以𝑂𝑃⃗⃗⃗ ⊥ 𝐵𝑀⃗⃗⃗⃗ ,即 OP⊥BM

志鸿优化系列丛书 志鸿优化网,永远提供更新的: 丛书主编任志湖。 http://www.zhyh.org 所以直线BM与OP所成的角为2 7.己知点E,F分别在正方体ABCD-AB1C1D1的棱BB1,CC1上,且B1E-2EB,CF-2FC1,则平面AEF与 平面ABCD的夹角的正切值为 图案 解析如图,建立空间直角坐标系 D 设正方体的棱长为1,则41,00,111F(0,1),所以正=(0,1),丽=(1,0》 平面ABCD的一个法向量为n1=(0,0,1) 设平面AEF的法向量为2=(x,), 由n2AE=0,2EF=0,可得平面AEF的一个法向量为2=(1,-1,3) 所以csn>将=要 设平面AEF与平面ABCD的夫角为a则c0sa=c0s<,3匹从而sina= 11 11 ⑦ 所以tanu=3 8.如图,在四面体ABCD中,CA=CB=CD=BD=2,AB=AD=√Z.求异面直线AB与CD所成角的余弦值. B 解如图,取BD的中点O,连接OA,0C,则由题意知,OALBD,OC⊥BD,0A=1,OC=V3 又CA=2,所以OA2+OC2=CA2,所以OA⊥OC 4
4 所以直线 BM 与 OP 所成的角为π 2 . 7.已知点 E,F 分别在正方体 ABCD-A1B1C1D1的棱 BB1,CC1 上,且 B1E=2EB,CF=2FC1,则平面 AEF 与 平面 ABCD 的夹角的正切值为 . 答案: √2 3 解析:如图,建立空间直角坐标系. 设正方体的棱长为 1,则 A(1,0,0),E 1,1,1 3 ,F(0,1, 2 3 ),所以𝐴𝐸⃗⃗⃗ = (0,1, 1 3 ) ,𝐸𝐹⃗⃗ = (-1,0, 1 3 ). 平面 ABCD 的一个法向量为 n1=(0,0,1). 设平面 AEF 的法向量为 n2=(x,y,z), 由 n2·𝐴𝐸⃗⃗⃗ =0,n2·𝐸𝐹⃗⃗ =0,可得平面 AEF 的一个法向量为 n2=(1,-1,3). 所以 cos= 𝑛1·𝑛2 |𝑛1||𝑛2| = 3√11 11 . 设平面 AEF 与平面 ABCD 的夹角为 α,则 cos α=|cos|=3√11 11 ,从而 sin α= √22 11 . 所以 tan α= √2 3 . 8. 如图,在四面体 ABCD 中,CA=CB=CD=BD=2,AB=AD=√2.求异面直线 AB 与 CD 所成角的余弦值. 解:如图,取 BD 的中点 O,连接 OA,OC,则由题意知,OA⊥BD,OC⊥BD,OA=1,OC=√3. 又 CA=2,所以 OA2+OC2=CA2 ,所以 OA⊥OC

志鸿优化系列丛书 志鸿优化网永远提供更新的! 丛书主编任志河。 http://www.zhyh.org 以O为原点,OB,OC,OA所在直线分别为x轴、y轴、:轴,建立空间直角坐标系, 则B(1,0,0),D(-1,0,0),C(0,V3,0),A0,0,1)2 所以BA-(-1,0,1),CD=(1,-3,0) 设异面直线AB与CD所成的角为O, 则os0-6osAD1恶-号 BAICDI 故异面直线AB与CD所成角的余弦值为 9.如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FEAB⊥AD,M为EC的中 点,AF=AB=BC=FE-2AD. (I)求异面直线BF与DE所成的角的大小: (2)求证:平面AMDL平面CDE (3)求平面ABCD与平面CDE的夹角的余弦值. (1)解图如图,以A为原点,AB,AD,AF所在直线分别为x轴、y轴、z轴,建立空间直角坐标系 设AB=1,则B(1,0,0),C(1,1,0),D0,2,0),E0,1,1),F(0,0,1), 所以BF-(-1,0,1),D元=(0,-1,1) 设BF与DE所成的角为O, 则coscos1=2 BFIDEI 所以0=60° 所以异面直线BF与DE所成的角为60° (2应明(1)知,丽.1,正10,1, AD=(0,2,0),所以C正.AM=0,CE.AD-0 5
5 以 O 为原点,OB,OC,OA 所在直线分别为 x 轴、y 轴、z 轴,建立空间直角坐标系, 则 B(1,0,0),D(-1,0,0),C(0,√3,0),A(0,0,1), 所以𝐵𝐴⃗⃗⃗ =(-1,0,1),𝐶𝐷⃗⃗⃗ =(-1,-√3,0). 设异面直线 AB 与 CD 所成的角为 θ, 则 cos θ=|cos|=|𝐵𝐴⃗⃗⃗⃗⃗ ·𝐶𝐷⃗⃗⃗⃗⃗ | |𝐵𝐴⃗⃗⃗⃗⃗ ||𝐶𝐷⃗⃗⃗⃗⃗ | = √2 4 . 故异面直线 AB 与 CD 所成角的余弦值为√2 4 . 9.如图,在五面体 ABCDEF 中,FA⊥平面 ABCD,AD∥BC∥FE,AB⊥AD,M 为 EC 的中 点,AF=AB=BC=FE=1 2 AD. (1)求异面直线 BF 与 DE 所成的角的大小; (2)求证:平面 AMD⊥平面 CDE; (3)求平面 ABCD 与平面 CDE 的夹角的余弦值. (1)解:如图,以 A 为原点,AB,AD,AF 所在直线分别为 x 轴、y 轴、z 轴,建立空间直角坐标系. 设 AB=1,则 B(1,0,0),C(1,1,0),D(0,2,0),E(0,1,1),F(0,0,1),M 1 2 ,1,1 2 . 所以𝐵𝐹⃗⃗⃗ =(-1,0,1),𝐷𝐸⃗⃗⃗⃗ =(0,-1,1). 设 BF 与 DE 所成的角为 θ, 则 cos θ=|cos|=|𝐵𝐹⃗⃗⃗⃗⃗ ·𝐷𝐸⃗⃗⃗⃗⃗ | |𝐵𝐹⃗⃗⃗⃗⃗ ||𝐷𝐸⃗⃗⃗⃗⃗ | = 1 2 , 所以 θ=60°. 所以异面直线 BF 与 DE 所成的角为 60°. (2)证明:由(1)知,𝐴𝑀⃗⃗⃗⃗ = 1 2 ,1,1 2 ,𝐶𝐸⃗⃗ =(-1,0,1), 𝐴𝐷⃗⃗⃗⃗ =(0,2,0),所以𝐶𝐸⃗⃗ · 𝐴𝑀⃗⃗⃗⃗ =0,𝐶𝐸⃗⃗ · 𝐴𝐷⃗⃗⃗⃗ =0

志鸿优化系列丛书 志鸿优化网永远提供更新的! 丛书主编任志河。 http://www.zhyh.org 所以CE⊥AM,CE⊥AD,即CE⊥AM,CE⊥AD 又AM∩AD=A.所以CE⊥平面AMD 又CEc平面CDE, 所以平面AMD⊥平面CDE. (3解设平面CDE的法向量为n=(xy,, 剥8脚+2=8取n叫11n '(n-DE=0, 因为FAL⊥平面ABCD,所以AF=(0,0,1)为平面ABCD的一个法向量. 设平面ABCD与平面CDE的夹角为O, 剥cos0 dcos-n.F--=9 故平面MBCD与平面CDE的夫角的余弦值为号 拓展提高 1.在长方体ABCD-A1B1C1D1中,己知B1C和CD与底面所成的角分别为60°和45°,则异面直线 B1C和CD所成角的余弦值为() AS B.@ 答案A 解析由题意可知,∠CB1C=60°,∠DCD1-45°,所以CC=V3B1C1,CD1=DD1. 设B1C=1, 则CC1-V3,CD1=V3 如图,以A1为原点,建立空间直角坐标系,则B1(V3,0,0),C(3,1,V3),C(3,1,0),D0,1,V3),所以 B1C=(0,1,3),C1D=(-V30,V3). 设B1C和CD所成的角为O, 则cos0-cos=5 BICIC D 6
6 所以𝐶𝐸⃗⃗ ⊥ 𝐴𝑀⃗⃗⃗⃗ , 𝐶𝐸⃗⃗ ⊥ 𝐴𝐷⃗⃗⃗⃗ ,即 CE⊥AM,CE⊥AD. 又 AM∩AD=A,所以 CE⊥平面 AMD. 又 CE⊂平面 CDE, 所以平面 AMD⊥平面 CDE. (3)解:设平面 CDE 的法向量为 n=(x,y,z), 则{ 𝑛·𝐶𝐸⃗⃗ = 0, 𝑛·𝐷𝐸⃗⃗⃗⃗ = 0, 即 { -𝑥 + 𝑧 = 0, -𝑦 + 𝑧 = 0, 取 n=(1,1,1). 因为 FA⊥平面 ABCD,所以𝐴𝐹⃗⃗⃗ =(0,0,1)为平面 ABCD 的一个法向量. 设平面 ABCD 与平面 CDE 的夹角为 θ, 则 cos θ=|cos|=|𝑛·𝐴𝐹⃗⃗⃗⃗ | |𝑛||𝐴𝐹⃗⃗⃗⃗ | = √3 3 . 故平面 ABCD 与平面 CDE 的夹角的余弦值为√3 3 . 拓展提高 1.在长方体 ABCD-A1B1C1D1中,已知 B1C 和 C1D 与底面所成的角分别为 60°和 45°,则异面直线 B1C 和 C1D 所成角的余弦值为( ) A. √6 4 B. √10 4 C. √3 2 D. √3 4 答案:A 解析:由题意可知,∠CB1C1=60°,∠DC1D1=45°,所以 CC1=√3B1C1,C1D1=DD1. 设 B1C1=1, 则 CC1=√3,C1D1=√3. 如图,以 A1 为原点,建立空间直角坐标系,则 B1(√3,0,0),C(√3,1,√3),C1(√3,1,0),D(0,1,√3),所以 𝐵⃗⃗ 1 ⃗⃗𝐶 =(0,1,√3),𝐶⃗⃗ 1 ⃗𝐷⃗ =(-√3,0,√3). 设 B1C 和 C1D 所成的角为 θ, 则 cos θ=|cos|=|𝐵⃗⃗⃗ 1 ⃗⃗⃗𝐶⃗ ·𝐶⃗⃗⃗ 1 ⃗⃗⃗𝐷⃗⃗ | |𝐵⃗⃗⃗ 1 ⃗⃗⃗𝐶⃗ ||𝐶⃗⃗⃗ 1 ⃗⃗⃗𝐷⃗⃗ | = √6 4

志鸿优化系列丛书 志鸿优化网,永远提供更新的: 丛书主编任志河。 http://www.zhyh.org 故异面直钱B,C和CD所成角的余弦值为9 2.如图,在四棱锥P-ABCD中,底面ABCD为菱形,且PA⊥平面ABCD,PA=AD=AC,F为PC的中点,则 平面PBC与平面BDF的夹角的正切值为() 号 B 4 C D23 3 3 含案p 解析设AC与BD交于点O,连接OF,则由题意可知,OB,OC,OF两两互相垂直. 以O为原点,OB,OC,OF所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,如图所示 设PA=AD=AC=1,则BD=V3, 所以0o.00,0d,rog,cog0)p0) 所以元-0,1-1r-,元-(0号d 易知OC=(0,2,0)为平面BDF的一个法向量. 设平面PBC的法向量为n=(xy,) (y-z=0, 则n严=0即区」 n=0,2x+=0,取nl,v3v 设平面PBC与平面BDF的夹角为O, 则cos0-cosn元1- 所以n0-29m0=29 3 所以平面PBC与平面BDF的夹角的正切值为 2 7
7 故异面直线 B1C 和 C1D 所成角的余弦值为√6 4 . 2. 如图,在四棱锥 P-ABCD 中,底面 ABCD 为菱形,且 PA⊥平面 ABCD,PA=AD=AC,F 为 PC 的中点,则 平面 PBC 与平面 BDF 的夹角的正切值为( ) A. √3 6 B. √3 4 C. √3 3 D. 2√3 3 答案:D 解析:设 AC 与 BD 交于点 O,连接 OF,则由题意可知,OB,OC,OF 两两互相垂直. 以 O 为原点,OB,OC,OF 所在直线分别为 x 轴、y 轴、z 轴,建立空间直角坐标系,如图所示. 设 PA=AD=AC=1,则 BD=√3, 所以 O(0,0,0),B √3 2 ,0,0 ,F 0,0,1 2 ,C 0,1 2 ,0 ,P(0,- 1 2 ,1). 所以𝑃𝐶⃗⃗ =(0,1,-1),𝐵𝐶⃗⃗⃗ = - √3 2 , 1 2 ,0 ,⃗𝑂𝐶⃗⃗ = 0,1 2 ,0 . 易知⃗𝑂𝐶⃗⃗ = (0, 1 2 ,0)为平面 BDF 的一个法向量. 设平面 PBC 的法向量为 n=(x,y,z). 则{ 𝑛·𝑃𝐶⃗⃗ = 0, 𝑛·𝐵𝐶⃗⃗⃗ = 0, 即{ 𝑦-𝑧 = 0, - √3 2 𝑥 + 1 2 𝑦 = 0, 取 n=(1,√3,√3). 设平面 PBC 与平面 BDF 的夹角为 θ, 则 cos θ=|cos|=√21 7 . 所以 sin θ= 2√7 7 ,tan θ= 2√3 3 . 所以平面 PBC 与平面 BDF 的夹角的正切值为2√3 3
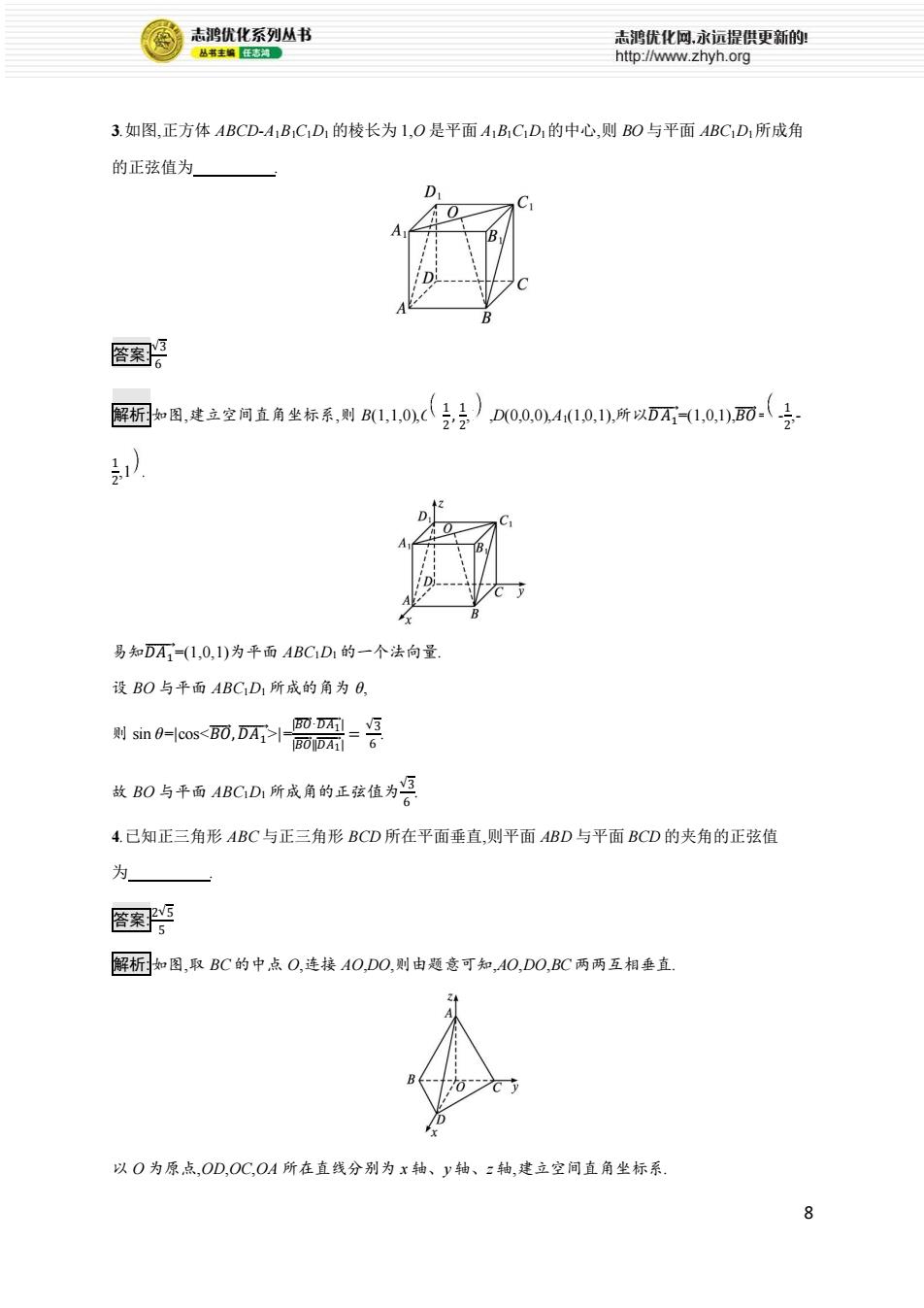
志鸿优化系列丛书 志鸿优化网永远提供更新的! 丛书主编任志河。 http://www.zhyh.org 3.如图,正方体ABCD-A1B1C1D1的棱长为1,O是平面A1BC1D1的中心,则BO与平面ABC1D1所成角 的正弦值为」 A B 含案 解图,建立空间直角坐标系,则B(1,10,c2)D00,04(10,1,所以DA-10,1),0.之 以 D 易知DA=(1,0,1)为平面ABCD1的一个法向量 设BO与平面ABC1D1所成的角为0, 剥血as0,所需-号 故B0与平面ABCD1所成角的正弦值为 4.己知正三角形ABC与正三角形BCD所在平面垂直,则平面ABD与平面BCD的夹角的正弦值 为 图系 解析如图,取BC的中点O,连接AO,DO,则由题意可知,AO,DO,BC两两互相垂直. 以O为原点,OD,OC,OA所在直线分别为x轴、y轴、:轴,建立空间直角坐标系. 8
8 3.如图,正方体 ABCD-A1B1C1D1 的棱长为 1,O 是平面 A1B1C1D1的中心,则 BO 与平面 ABC1D1所成角 的正弦值为 . 答案: √3 6 解析:如图,建立空间直角坐标系,则 B(1,1,0),O 1 2 , 1 2 ,1 ,D(0,0,0),A1(1,0,1),所以𝐷𝐴1 ⃗⃗⃗⃗ =(1,0,1),𝐵𝑂⃗⃗⃗⃗ = - 1 2 ,- 1 2 ,1 . 易知𝐷𝐴1 ⃗⃗⃗⃗ =(1,0,1)为平面 ABC1D1 的一个法向量. 设 BO 与平面 ABC1D1 所成的角为 θ, 则 sin θ=|cos|=|𝐵𝑂⃗⃗⃗⃗⃗ ·𝐷𝐴1 ⃗⃗⃗⃗⃗⃗⃗⃗ | |𝐵𝑂⃗⃗⃗⃗⃗ ||𝐷𝐴1 ⃗⃗⃗⃗⃗⃗⃗⃗ | = √3 6 . 故 BO 与平面 ABC1D1 所成角的正弦值为√3 6 . 4.已知正三角形 ABC 与正三角形 BCD 所在平面垂直,则平面 ABD 与平面 BCD 的夹角的正弦值 为 . 答案: 2√5 5 解析:如图,取 BC 的中点 O,连接 AO,DO,则由题意可知,AO,DO,BC 两两互相垂直. 以 O 为原点,OD,OC,OA 所在直线分别为 x 轴、y 轴、z 轴,建立空间直角坐标系

志鸿优化系列丛书 志鸿优化网,永远提供更新的! 丛书主编任志湖。 http://www.zhyh.org 设BC=1,则40,090号)五(0.0】 所以0=,0盟,m-2,丽-〈0 显然O丽-).0,)为平面BCD的一个法向量 设平面ABD的法向量为n=(xy,), 则n丽=0即 y+2 =0 n BD=0, 2x+iy=0. 取x=1,则y=-V3,=1. 所以n=(1,-V3,1)为平面ABD的一个法向量. 设平面ABD与平面BCD的夹角为O, 则cos0 -cos0),若平面a与平面xOy的 夹角为45°,则a= 含案光 解析由题意可知,A正(-3,4,0),AC=(-3,0,a,平面x0y的一个法向量为n=(00,1) 设平面a的法向量为u=(xy,z), 则u亚=0即3x+y=0 '(uAC=0, -3x+az=0, 所以3x=4y=ae 取u-(传异1) 由题意得cos= 1一= a2,a2 23 √+6+1 又0,故a号 6.如图,正方形ACDE所在的平面与平面ABC垂直,M为CE与AD的交点,AC⊥BC,且AC=BC 9
9 设 BC=1,则 A 0,0,√3 2 ,B 0,- 1 2 ,0 ,D √3 2 ,0,0 , 所以𝑂𝐴⃗⃗⃗ = 0,0,√3 2 ,𝐵𝐴⃗⃗⃗ = 0,1 2 , √3 2 ,𝐵𝐷⃗ ⃗ = √3 2 , 1 2 ,0 . 显然𝑂𝐴⃗⃗⃗ = 0,0,√3 2 为平面 BCD 的一个法向量. 设平面 ABD 的法向量为 n=(x,y,z), 则{ 𝑛·𝐵𝐴⃗⃗⃗ = 0, 𝑛·𝐵𝐷⃗ ⃗ = 0, 即{ 1 2 𝑦 + √3 2 𝑧 = 0, √3 2 𝑥 + 1 2 𝑦 = 0. 取 x=1,则 y=-√3,z=1. 所以 n=(1,-√3,1)为平面 ABD 的一个法向量. 设平面 ABD 与平面 BCD 的夹角为 θ, 则 cos θ=|cos|=|𝑛·𝑂𝐴⃗⃗⃗⃗⃗ | |𝑛||𝑂𝐴⃗⃗⃗⃗⃗ | = √5 5 . 所以 sin θ= 2√5 5 . 故平面 ABD 与平面 BCD 的夹角的正弦值为2√5 5 . 5.在空间中,已知平面 α 过点 A(3,0,0)和 B(0,4,0)及 z 轴上一点 C(0,0,a)(a>0),若平面 α 与平面 xOy 的 夹角为 45°,则 a= . 答案: 12 5 解析:由题意可知,𝐴𝐵⃗⃗⃗ =(-3,4,0),𝐴𝐶⃗⃗ =(-3,0,a),平面 xOy 的一个法向量为 n=(0,0,1). 设平面 α 的法向量为 u=(x,y,z), 则{ 𝑢·𝐴𝐵⃗⃗⃗ = 0, 𝑢·𝐴𝐶⃗⃗ = 0, 即{ -3𝑥 + 4𝑦 = 0, -3𝑥 + 𝑎𝑧 = 0, 所以 3x=4y=az. 取 u=( 𝑎 3 , 𝑎 4 ,1). 由题意得|cos|= 1 √𝑎2 9 + 𝑎2 16+1 = √2 2 , 又 a>0,故 a= 12 5 . 6. 如图,正方形 ACDE 所在的平面与平面 ABC 垂直,M 为 CE 与 AD的交点,AC⊥BC,且 AC=BC

志鸿优化系列丛书 志鸿优化网永远提供更新的! 丛书主编任志湖。 http://www.zhyh.org (I)求证:AML平面EBC (2)求直线AB与平面EBC所成的角的大小 解以A为原点,建立空间直角坐标系,如图所示 不妨设AC=2,则A0,0,0),M(0,1,1),B2,2,0),C(0,2,0),E(0,0,2) (1)证明:AM-(0,1,1),EC=(0,2,-2),CB=(2,0,0), ∴.AM.EC-0,AM.CE-0. ∴.AM⊥EC,AMLCB. 又ECNCB=C, ∴.AML平面EBC (2),AM⊥平面EBC ∴.AM=(0,1,1)为平面EBC的一个法向量 设直线AB与平面EBC所成的角为O, AB=(2,2,0), 如0-os丽,丽疆-号 ABIAMI ∴.0=30° ,∴.直线AB与平面EBC所成的角为30°· 挑h战创新 如图,四棱柱ABCD-A1B1C1D1的所有棱长都相等,ACOBD=O,A1C∩B1D1=O1,四边形ACC1A1和四 边形BDD1B1均为矩形 10
10 (1)求证:AM⊥平面 EBC; (2)求直线 AB 与平面 EBC 所成的角的大小. 解:以 A 为原点,建立空间直角坐标系,如图所示. 不妨设 AC=2,则 A(0,0,0),M(0,1,1),B(2,2,0),C(0,2,0),E(0,0,2). (1)证明:∵𝐴𝑀⃗⃗⃗⃗ =(0,1,1),𝐸𝐶⃗⃗ =(0,2,-2),𝐶𝐵⃗⃗⃗ =(2,0,0), ∴𝐴𝑀⃗⃗⃗⃗ · 𝐸𝐶⃗⃗ =0,𝐴𝑀⃗⃗⃗⃗ · 𝐶𝐵⃗⃗⃗ =0. ∴AM⊥EC,AM⊥CB. 又 EC∩CB=C, ∴AM⊥平面 EBC. (2)∵AM⊥平面 EBC, ∴𝐴𝑀⃗⃗⃗⃗ =(0,1,1)为平面 EBC 的一个法向量. 设直线 AB 与平面 EBC 所成的角为 θ, ∵𝐴𝐵⃗⃗⃗ =(2,2,0), ∴sin θ=|cos|=|𝐴𝐵⃗⃗⃗⃗⃗ ·𝐴𝑀⃗⃗⃗⃗⃗⃗ | |𝐴𝐵⃗⃗⃗⃗⃗ ||𝐴𝑀⃗⃗⃗⃗⃗⃗ | = 1 2 . ∴θ=30°. ∴直线 AB 与平面 EBC 所成的角为 30°. 挑战创新 如图,四棱柱 ABCD-A1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形 ACC1A1和四 边形 BDD1B1 均为矩形