
9.2.1总体取值规律的估计 课后·训练提升 基础巩固 1为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单 位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17刀,将其按从左到右的顺序分别编号 为第一组,第二组,…,第五组,根据试验数据制成的频率分布直方图如图所示己知第一组与第 二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为(). 补频率组距 0.36 0.24 0.16 0.08 02131415167舒张压Pa A.6 B.8 C.12 D.18 窨案 解标志愿者的总人数为 0,16+024x-50,故第三组人数为50×0,36×1=18,有疗效的人数为 20 18-6=12. 2.某校为了解高三学生的身体情况,抽取了100名女生的体重(单位:kg).将所得的数据整理后, 绘制出了频率分布直方图如图所示,则所抽取的女生中体重在区间[40,45)内的人数是(). ↑频率/组距 0.10 0.08 0.06 0.04 0.02 9045505560体重kg A.10 B.2 C.5 D.15 含答案A 解析由题图可知女生体重在区间[40,45)内的人数为0.02×5×100=10. 3.某校高一年级学生到校方式的条形统计图如图所示,根据图形可得出骑自行车人数占高一 年级学生总人数的( 人数 150 120 90 60 30 0 步行骑自行车坐公共到校方式 汽车 A.20% B.30% C.50% D.60% 答案B
9.2.1 总体取值规律的估计 课后· 基础巩固 1.为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单 位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号 为第一组,第二组,…,第五组,根据试验数据制成的频率分布直方图如图所示.已知第一组与第 二组共有 20 人,第三组中没有疗效的有 6 人,则第三组中有疗效的人数为( ). A.6 B.8 C.12 D.18 答案 C 解析志愿者的总人数为 20 (0.16+0.24)×1 =50,故第三组人数为 50×0.36×1=18,有疗效的人数为 18-6=12. 2.某校为了解高三学生的身体情况,抽取了 100 名女生的体重(单位:kg).将所得的数据整理后, 绘制出了频率分布直方图如图所示,则所抽取的女生中体重在区间[40,45)内的人数是( ). A.10 B.2 C.5 D.15 答案 A 解析由题图可知女生体重在区间[40,45)内的人数为 0.02×5×100=10. 3.某校高一年级学生到校方式的条形统计图如图所示,根据图形可得出骑自行车人数占高一 年级学生总人数的( ). A.20% B.30% C.50% D.60% 答案 B

解标某校高一年级学生总数为60+90+150=300(人),骑自行车人数为90,骑自行车人数占高 一年级学生总数的百分比为器×100%-30% 4.某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布扇形 图、“90后”从事互联网行业岗位分布条形图如图所示,则下列结论中不一定正确的是() 注:“90后”指1990年及以后出生,“80后”指1980-1989年之间出生,80前”指1979年及以前 出生 “80前”3% “90后”56% 80后”41% “90后”从事互联网行业岗位分布图 技术口 ☐39.6% 运营 ☐17% 市场 013.2% 设计[ 门12.3% 职能0 ☐9.8% 产品☐6.5% 其他☐1.6% A.互联网行业从业人员中90后”占一半以上 B.互联网行业中从事技术岗位的90后”的人数超过总人数的20% C.互联网行业中从事运营岗位的90后”比从事运营岗位的“80前”多 D.互联网行业中从事运营岗位的90后”比从事运营岗位的“80后”多 答案D 解析对于选项A,互联网行业从业人员中“90后”占56%,占一半以上,该选项正确 对于选项B,互联网行业中从事技术岗位的90后”的人数占总人数的39.6%×56%=22.176%, 超过总人数的20%,该选项正确. 对于选项C,互联网行业中从事运营岗位的“90后”占总人数的56%×17%-9.52%大于互联网 行业中“80前”所占比例,该选项正确. 对于选项D,互联网行业中从事运营岗位的“90后”占总人数的56%×17%=9.52%,互联网行业 中“80后”占总人数的41%,即互联网行业中从事运营岗位的“90后”不一定比从事运营岗位 的“80后”多.该选项不正确. 5.对某种电子元件使用寿命进行跟踪调查,所得样本频率分布直方图如图所示.由图可知,这一 批电子元件中寿命在区间[100,300)内的电子元件的数量与寿命在区间[300,600]上的电子元 件的数量的比是(). 频率组距 250 400 3 2000 2000 100200300400500600寿命/h A.12 B.13 C.14 D.1.6 答案
解析某校高一年级学生总数为 60+90+150=300(人),骑自行车人数为 90,骑自行车人数占高 一年级学生总数的百分比为 90 300×100%=30%. 4.某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布扇形 图、“90 后”从事互联网行业岗位分布条形图如图所示,则下列结论中不一定正确的是( ). 注:“90 后”指 1990 年及以后出生,“80 后”指 1980~1989 年之间出生,“80 前”指 1979 年及以前 出生. A.互联网行业从业人员中“90 后”占一半以上 B.互联网行业中从事技术岗位的“90 后”的人数超过总人数的 20% C.互联网行业中从事运营岗位的“90 后”比从事运营岗位的“80 前”多 D.互联网行业中从事运营岗位的“90 后”比从事运营岗位的“80 后”多 答案 D 解析对于选项 A,互联网行业从业人员中“90 后”占 56%,占一半以上,该选项正确. 对于选项 B,互联网行业中从事技术岗位的“90 后”的人数占总人数的 39.6%×56%=22.176%, 超过总人数的 20%,该选项正确. 对于选项 C,互联网行业中从事运营岗位的“90 后”占总人数的 56%×17%=9.52%,大于互联网 行业中“80 前”所占比例,该选项正确. 对于选项 D,互联网行业中从事运营岗位的“90 后”占总人数的 56%×17%=9.52%,互联网行业 中“80 后”占总人数的 41%,即互联网行业中从事运营岗位的“90 后”不一定比从事运营岗位 的“80 后”多.该选项不正确. 5.对某种电子元件使用寿命进行跟踪调查,所得样本频率分布直方图如图所示.由图可知,这一 批电子元件中寿命在区间[100,300)内的电子元件的数量与寿命在区间[300,600]上的电子元 件的数量的比是( ). A.1∶2 B.1∶3 C.1∶4 D.1∶6 答案 C

解韧由题意,寿命在区间[10,300)内的电子元件的领率为100200+20)-0.2,寿命在区 间[30,60]上的电子元件的频率为10×品0+高+2)-0.8则寿命在区间[10,30)内的 电子元件的数量与寿命在区间[300,600]上的电子元件的数量的比是0.2,0.8=1:4 ↑频率/组距 0.035 0.030 0.020 0.010 0.005 100110120130140150身高/cm 6.从某小学随机抽取100名学生,将他们的身高数据(单位:cm)按 [100,110),[110,120),120,130),[130,140),140,150]分组,绘制成频率分布直方图如图所示.从身 高在区间[120,130),[130,140),[140,150)内的学生中,用分层随机抽样的方法抽取18人参加一 项活动,则从身高在区间[140,150]上的学生中选取的人数应为( A.3 B.4 C.5 D.6 含案A 解桐各组频率等于各组矩形的面积,因此身高在区间[120,130),[130,140),[140,150)内的频率 分别为0.3,0.2,0.1,身高在区间[120,130),[130,140),[140,150)内的频数分别为30,20,10,分层随 机抽样的比例为080=品所以从身高在区间同140,150上的学生中选取的人教为 18 10×品-3 7.为了解某校高三学生的身体状况,用分层随机抽样的方法抽取部分男生和女生的体重,将男 生的体重数据整理后,绘制出频率分布直方图如图所示.已知图中从左到右前三个小组频率之 比为1‘2:3,第二小组频数为12,若全校男生、女生比例为3:2,则全校抽取学生数为 频率/组距 0.0375 0.0125 005560657075体重kg 客案0 解析由题图可知,第四组与第五组的频率和为(0.0125+0.0375)×50.25,因为从左到右前三个 小组频率之比为1:2:3,第二小组频数为12,所以前三个小组的频数为36,从而男生有 3 0.25=48(人) 又国为全校男生、女生比例为3:2,所以全校抽取学生数为48×-80, 8.某校八年级学生参加“史地生会考”,八年级(1)班25名学生的成绩(满分为100分)统计如 下:90,74,88,65,98,75,81,42,85,70,55,80,95,88,72,87,60,56,76,66,7872,82,63,100
解析由题意,寿命在区间[100,300)内的电子元件的频率为 100×( 1 2 000 + 3 2 000)=0.2,寿命在区 间[300,600]上的电子元件的频率为 100×( 1 400 + 1 250 + 3 2 000)=0.8,则寿命在区间[100,300)内的 电子元件的数量与寿命在区间[300,600]上的电子元件的数量的比是 0.2∶0.8=1∶4. 6.从某小学随机抽取 100 名学生,将他们的身高数据(单位:cm)按 [100,110),[110,120),[120,130),[130,140),[140,150]分组,绘制成频率分布直方图如图所示.从身 高在区间[120,130),[130,140),[140,150)内的学生中,用分层随机抽样的方法抽取 18 人参加一 项活动,则从身高在区间[140,150]上的学生中选取的人数应为( ). A.3 B.4 C.5 D.6 答案 A 解析各组频率等于各组矩形的面积,因此身高在区间[120,130),[130,140),[140,150)内的频率 分别为 0.3,0.2,0.1,身高在区间[120,130),[130,140),[140,150)内的频数分别为 30,20,10,分层随 机抽样的比例为 18 30+20+10 = 3 10.所以从身高在区间[140,150]上的学生中选取的人数为 10× 3 10=3. 7.为了解某校高三学生的身体状况,用分层随机抽样的方法抽取部分男生和女生的体重,将男 生的体重数据整理后,绘制出频率分布直方图如图所示.已知图中从左到右前三个小组频率之 比为 1∶2∶3,第二小组频数为 12,若全校男生、女生比例为 3∶2,则全校抽取学生数为 . 答案 80 解析由题图可知,第四组与第五组的频率和为(0.012 5+0.037 5)×5=0.25,因为从左到右前三个 小组频率之比为 1∶2∶3,第二小组频数为 12,所以前三个小组的频数为 36,从而男生有 36 1-0.25=48(人). 又因为全校男生、女生比例为 3∶2,所以全校抽取学生数为 48× 5 3 =80. 8.某校八年级学生参加“史地生会考”,八年级(1)班 25 名学生的成绩(满分为 100 分)统计如 下:90,74,88,65,98,75,81,42,85,70,55,80,95,88,72,87,60,56,76,66,78,72,82,63,100
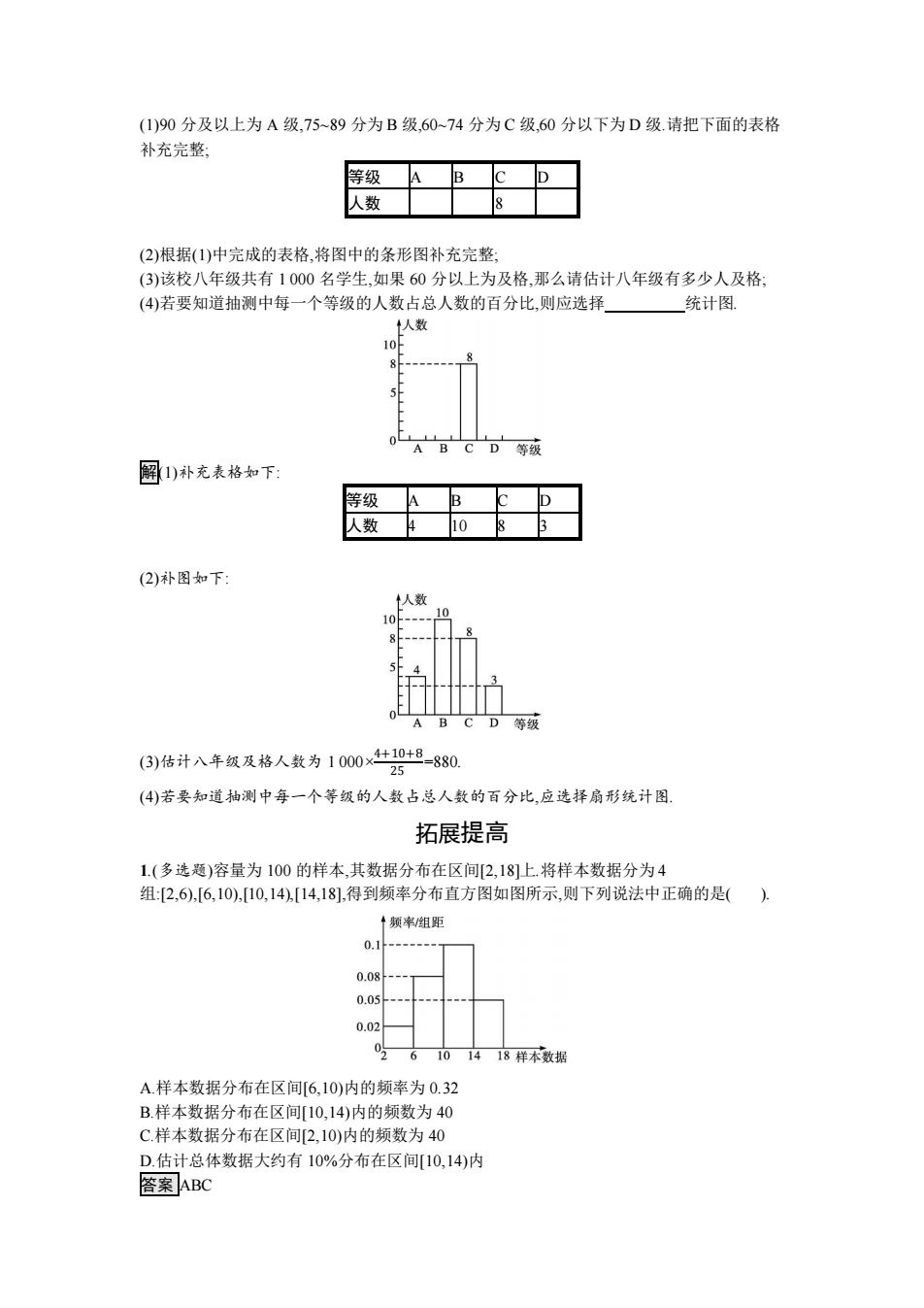
(1)90分及以上为A级,75~89分为B级,60~74分为C级,60分以下为D级.请把下面的表格 补充完整 等级 B D 人数 (2)根据(1)中完成的表格,将图中的条形图补充完整, (3)该校八年级共有1000名学生,如果60分以上为及格,那么请估计八年级有多少人及格: (4)若要知道抽测中每一个等级的人数占总人数的百分比,则应选择 统计图 人数 10 BCD等级 园)补充表格如下: 等级 A D 人数 4 10 (2)补图如下: 人数 10 10 ABCD等级 (3)估计八年级及格人数为1000×4±10+8-880. 25 (4)若要知道抽测中每一个等级的人数占总人数的百分比,应选择扇形统计图. 拓展提高 1.(多选题)容量为100的样本,其数据分布在区间[2,18]上.将样本数据分为4 组:[2,6),[6,10),[10,14),[14,18],得到频率分布直方图如图所示,则下列说法中正确的是() ↑频率组距 0.1 0.08- 0.05 0.02 6101418样本数据 A.样本数据分布在区间[6,10)内的频率为0.32 B.样本数据分布在区间[10,14)内的频数为40 C.样本数据分布在区间[2,10)内的频数为40 D.估计总体数据大约有10%分布在区间[10,14)内 答案ABC
(1)90 分及以上为 A 级,75~89 分为 B 级,60~74 分为 C 级,60 分以下为 D 级.请把下面的表格 补充完整; 等级 A B C D 人数 8 (2)根据(1)中完成的表格,将图中的条形图补充完整; (3)该校八年级共有 1 000 名学生,如果 60 分以上为及格,那么请估计八年级有多少人及格; (4)若要知道抽测中每一个等级的人数占总人数的百分比,则应选择 统计图. 解(1)补充表格如下: 等级 A B C D 人数 4 10 8 3 (2)补图如下: (3)估计八年级及格人数为 1 000× 4+10+8 25 =880. (4)若要知道抽测中每一个等级的人数占总人数的百分比,应选择扇形统计图. 拓展提高 1.(多选题)容量为 100 的样本,其数据分布在区间[2,18]上.将样本数据分为 4 组:[2,6),[6,10),[10,14),[14,18],得到频率分布直方图如图所示,则下列说法中正确的是( ). A.样本数据分布在区间[6,10)内的频率为 0.32 B.样本数据分布在区间[10,14)内的频数为 40 C.样本数据分布在区间[2,10)内的频数为 40 D.估计总体数据大约有 10%分布在区间[10,14)内 答案 ABC

解析由题图可知,样本数据分布在区间[6,10)内的频率为0.08×4=0.32,所以A正确样本数据 分布在区间[10,14)内的频数为100×(0.1×4)=40,所以B正确.样本数据分布在区间[2,10)内的 频数为100×(0.02+0.08)×4=40,所以C正确.估计总体数据分布在区间[10,14)内的比例为 0.1×4=0.4=40%.所以D错误.故选ABC. 2.某所学校一个学期的开支分布的扇形图如图①所示,该学期的水、电、交通开支(单位:万 元)如图②所示,则该学期的水电费开支占总开支的百分比为( 其他支出劳务支出 500 450 450 水、电、 5%100 400 交通支出 330 20% 办公 300 30% 支出 15% 150 维修支出 20% 50 教研训辅支出 水 电 交通 ① ② A.12.25% B.16.25% C.11.25% D.9.25% 答案B 解韧由题图②知,水、电支出占水、电、交通支出的比例为,200+450=马由题图⑦知, 200+450+150 16 水、电、交通支出占学校一个学期总开支的比例为因此,该学期的水电费开支占总开支的 百分比为号×-品-1625%故选B 3.统计某校n名学生的某次数学同步练习成绩(满分150分),根据成绩分数依次分成六 组:[90,100),[100,110),[110,120),[120,130),[130,140),[140,150],得到频率分布直方图如图所示. 若不低于140分的人数为110,给出四个结论:①m=0.031;②n=800:③100分以下的人数为60: ④分数在区间[120,140)内的人数超过总人数的一半.其中结论正确的是(). ↑频率组距 0.020 0.016 0.011 0.006 90100110120130140150分数 A.①② B.①③ C.②③ D.②④ 答案B 解桐由题意,根据频率分布直方图的性质得10(0.006+0.016+0.020+m+0.016+0.011)=1,解得 m=0.031.故①正确; 国为不低于140分的频率为001×10=0.1山,所以n品100,故②错误 由100分以下的频率为0.006×10=0.06,所以100分以下的人数为1000×0.06=60,故③正确; 分数在区间[120,140)内的人数占0.031×10+0.016×10=0.47,占小半,故@④猎误.所以说法正确 的是①③ 4.为了解学生的身体状况,某校随机抽取了一批学生测量体重经统计,这批学生的体重数据 (单位:千克)全部介于45至70之间.将数据分成以下5组:第1组[45,50),第2组[50,55),第3 组[55,60),第4组[60,65),第5组[65,70],得到频率分布直方图如图所示,则a= 现采
解析由题图可知,样本数据分布在区间[6,10)内的频率为 0.08×4=0.32,所以 A 正确.样本数据 分布在区间[10,14)内的频数为 100×(0.1×4)=40,所以 B 正确.样本数据分布在区间[2,10)内的 频数为 100×(0.02+0.08)×4=40,所以 C 正确.估计总体数据分布在区间[10,14)内的比例为 0.1×4=0.4=40%,所以 D 错误.故选 ABC. 2.某所学校一个学期的开支分布的扇形图如图①所示,该学期的水、电、交通开支(单位:万 元)如图②所示,则该学期的水电费开支占总开支的百分比为( ). A.12.25% B.16.25% C.11.25% D.9.25% 答案 B 解析由题图②知,水、电支出占水、电、交通支出的比例为 200+450 200+450+150 = 13 16,由题图①知, 水、电、交通支出占学校一个学期总开支的比例为1 5 ,因此,该学期的水电费开支占总开支的 百分比为13 16 × 1 5 = 13 80=16.25%.故选 B. 3.统计某校 n 名学生的某次数学同步练习成绩(满分 150 分),根据成绩分数依次分成六 组:[90,100),[100,110),[110,120),[120,130),[130,140),[140,150],得到频率分布直方图如图所示. 若不低于 140 分的人数为 110,给出四个结论:①m=0.031;②n=800;③100 分以下的人数为 60; ④分数在区间[120,140)内的人数超过总人数的一半.其中结论正确的是( ). A.①② B.①③ C.②③ D.②④ 答案 B 解析由题意,根据频率分布直方图的性质得 10(0.006+0.016+0.020+m+0.016+0.011)=1,解得 m=0.031.故①正确; 因为不低于 140 分的频率为 0.011×10=0.11,所以 n= 110 0.11=1 000,故②错误; 由 100 分以下的频率为 0.006×10=0.06,所以 100 分以下的人数为 1 000×0.06=60,故③正确; 分数在区间[120,140)内的人数占 0.031×10+0.016×10=0.47,占小半,故④错误.所以说法正确 的是①③. 4.为了解学生的身体状况,某校随机抽取了一批学生测量体重.经统计,这批学生的体重数据 (单位:千克)全部介于 45 至 70 之间.将数据分成以下 5 组:第 1 组[45,50),第 2 组[50,55),第 3 组[55,60),第 4 组[60,65),第 5 组[65,70],得到频率分布直方图如图所示,则 a= .现采

用分层随机抽样的方法,从第3,4,5组中随机抽取6名学生,则第3,4,5组抽取的学生人数依次 为 ↑频率组距 0.07 0.06 0.02 0.01 55055606570体重/千克 窨案.043,2,1 解桐由(0.01+0.02+a+0.06+0.07)×5-1,得a=0.04. 设第3,4,5组抽取的学生人数依次为x,y,二, 则xyz=0.060.04:0.02=321, 又x+y+2=6,所以x=3,y=2,2=1. 5.一工厂生产某种产品共计16800件,它们分别来自甲、乙、丙3条生产线.为检查这批产品 的质量,决定采用分层随机抽样的方法进行抽样已知从甲、乙、丙3条生产线抽取的产品个 数分别是a,b,c,且2b=a+c,则乙生产线生产了_ 件产品 答案5600 解析设甲、乙、丙3条生产线各自生产了T甲,T,T件产品,则a:b:c=T,:T,,T,即 品方前 b T甲+T丙=2T乙 又因为2b=a+c,所以 T甲+T乙+T丙=16800, 所以T2160=5600(件) 3 6.为增强市民节能环保意识,某市面向全市征召义务宣传志愿者,现从符合条件的500名志愿 者中随机抽取100名志愿者,他们的年龄情况如下表所示 分组(单位:岁) 频数 频率 20,25) 5 0.05 [25,30) ① 0.20 30,35) 35 ② [35,40) 30 0.30 40,451 10 0.10 合计 100 1.00 频率组距 0.08 0.07 0.06 0.05 .04 0.03 0.02 0.01 202530354045年龄/岁 (1)频率分布表中的①②位置应填什么数据?
用分层随机抽样的方法,从第 3,4,5 组中随机抽取 6 名学生,则第 3,4,5 组抽取的学生人数依次 为 . 答案 0.04 3,2,1 解析由(0.01+0.02+a+0.06+0.07)×5=1,得 a=0.04. 设第 3,4,5 组抽取的学生人数依次为 x,y,z, 则 x∶y∶z=0.06∶0.04∶0.02=3∶2∶1, 又 x+y+z=6,所以 x=3,y=2,z=1. 5.一工厂生产某种产品共计 16 800 件,它们分别来自甲、乙、丙 3 条生产线.为检查这批产品 的质量,决定采用分层随机抽样的方法进行抽样.已知从甲、乙、丙 3 条生产线抽取的产品个 数分别是 a,b,c,且 2b=a+c,则乙生产线生产了 件产品. 答案 5 600 解析设甲、乙、丙 3 条生产线各自生产了 T 甲,T 乙,T 丙件产品,则 a∶b∶c=T 甲∶T 乙∶T 丙,即 𝑎 𝑇甲 = 𝑏 𝑇乙 = 𝑐 𝑇丙 . 又因为 2b=a+c,所以{ 𝑇甲 + 𝑇丙 = 2𝑇乙 , 𝑇甲 + 𝑇乙 + 𝑇丙 = 16 800, 所以 T 乙= 16 800 3 =5 600(件). 6.为增强市民节能环保意识,某市面向全市征召义务宣传志愿者,现从符合条件的 500 名志愿 者中随机抽取 100 名志愿者,他们的年龄情况如下表所示. 分组(单位:岁) 频数 频率 [20,25) 5 0.05 [25,30) ① 0.20 [30,35) 35 ② [35,40) 30 0.30 [40,45] 10 0.10 合计 100 1.00 (1)频率分布表中的①②位置应填什么数据?

(2)补全频率分布直方图,再根据频率分布直方图估计这500名志愿者中年龄在区间[30,35)内 的人数 解1)设年龄在区间[25,30)内的频数为x,年龄在区间[30,35)内的频率为上 方法一:根据题意可得品-0,20,票y解得x-20,035,故⑦处应填20,②处应填0,35 方法二:由题意得5+x+35+30+10=100, 0.05+0.20+y+0.30+0.10=1.00, 解得x=20,y=0.35,故①处填20,②处填0.35. (2)由频率分布表知年龄在区间[25,30)内的频率是0.20,组距是5即题率-020-0.04 组距一 5 补全频率分布直方图如图所示, 频率组距 0.08 0.07-- 0.06--4- 0.05 0.04 0.03 0.02 0.01 02530354045年龄1岁 根据频率分布直方图估计这500名志愿者中年龄在区间[30,35)内的人数为500×0.35-175. 挑战创新 某高校在自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布 表如下 组号 分组 频数 频率 第1组 [160,165) 5 0.05 第2组 [165,170) ① 0.35 第3组 [170,175) 30 @ 第4组 [175,180) 20 0.20 第5组 180,1851 10 0.10 合计 100 1.00 (1)请先求出频率分布表中①②处应填写的数据,并完成频率分布直方图: ↑频率/组距 0.08 0.07 0.06 0.05 ----7- 0.04 0.03 0.02 0.01 160165170175180185成绩/分 (2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3,4,5组中用分层随机抽样的方 法抽取6名学生进入第二轮面试,求第3,4,5组每组各应抽取多少名学生进入第二轮面试 圆1)由题意可知,第2组的频数为0.35×100-35,第3组的频率为品-0.30,故①处填35,②处 填0.30
(2)补全频率分布直方图,再根据频率分布直方图估计这 500 名志愿者中年龄在区间[30,35)内 的人数. 解(1)设年龄在区间[25,30)内的频数为 x,年龄在区间[30,35)内的频率为 y. 方法一:根据题意可得 𝑥 100=0.20, 35 100=y,解得 x=20,y=0.35,故①处应填 20,②处应填 0.35. 方法二:由题意得 5+x+35+30+10=100, 0.05+0.20+y+0.30+0.10=1.00, 解得 x=20,y=0.35,故①处填 20,②处填 0.35. (2)由频率分布表知年龄在区间[25,30)内的频率是 0.20,组距是 5.即 频率 组距 = 0.20 5 =0.04. 补全频率分布直方图如图所示. 根据频率分布直方图估计这 500 名志愿者中年龄在区间[30,35)内的人数为 500×0.35=175. 挑战创新 某高校在自主招生考试成绩中随机抽取 100 名学生的笔试成绩,按成绩分组,得到的频率分布 表如下: 组号 分组 频数 频率 第 1 组 [160,165) 5 0.05 第 2 组 [165,170) ① 0.35 第 3 组 [170,175) 30 ② 第 4 组 [175,180) 20 0.20 第 5 组 [180,185] 10 0.10 合计 100 1.00 (1)请先求出频率分布表中①②处应填写的数据,并完成频率分布直方图; (2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第 3,4,5 组中用分层随机抽样的方 法抽取 6 名学生进入第二轮面试,求第 3,4,5 组每组各应抽取多少名学生进入第二轮面试. 解(1)由题意可知,第 2 组的频数为 0.35×100=35,第 3 组的频率为 30 100=0.30,故①处填 35,②处 填 0.30

频率分布直方图如图所示 ↑频率/组距 0.08--小----4--4- 0.07 0.06 0.05 0.04 0.03 0.02 0.01 160165170175180185成绩/分 (2)因为第3,4,5组共有60名学生,所以利用分层随机抽样在60名学生中抽取6名学生,抽样 比为品=六故第3组应抽取30×品-3(名)学生,第4组应抽取20品-2(名)学生,第5组应抽 取10×品=1(名)学生,所以第345组应抽取的学生人数分别为32,1
频率分布直方图如图所示. (2)因为第 3,4,5 组共有 60 名学生,所以利用分层随机抽样在 60 名学生中抽取 6 名学生,抽样 比为 6 60 = 1 10,故第 3 组应抽取 30× 1 10=3(名)学生,第 4 组应抽取 20× 1 10=2(名)学生,第 5 组应抽 取 10× 1 10=1(名)学生,所以第 3,4,5 组应抽取的学生人数分别为 3,2,1