8.5.3平面与平面平行 课后·训练提升 L.若平面a∥平面B,直线aca,点B∈B,则在平面B内过点B的所有直线中() A.不一定存在与a平行的直线 B.只有两条与a平行的直线 C.存在无数条与a平行的直线 D.存在唯一一条与a平行的直线 含案D 解桐因为直线α与点B可确定一个平面,该平面与平面B的交线即为在平面B内过点B,且 与直线α平行的直线,所以只有唯一一条。 2.在下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,则能得 到AB∥平面MNP的图形是( M 2 A.①② B.②④ C.②③ D.①④ 客案D 3.如图,在正方体ABCD-AB1CD1中,M,N,P分别是C1D1,BC,AD1的中点,则下列结论正确的 是() D A.MN∥AP B.MN∥BD1 C.MN∥平面BB1DD D.MN∥平面BDP 答案c 解析如图,取B1C的中点E,连接EM,NE,BD1,BD D P 因为M,N分别是CD1,BC的中点,所以BB1∥NE,BD1∥EM,又EM,NEt平面 BB1D1D,BB1B1D1C平面BB1D1D 所以EM∥平面BB1D1D,NE∥平面BB1DD 又EM∩NE=E,所以平面EMN∥平面BB1DD. 所以N∥平面BB1D1D
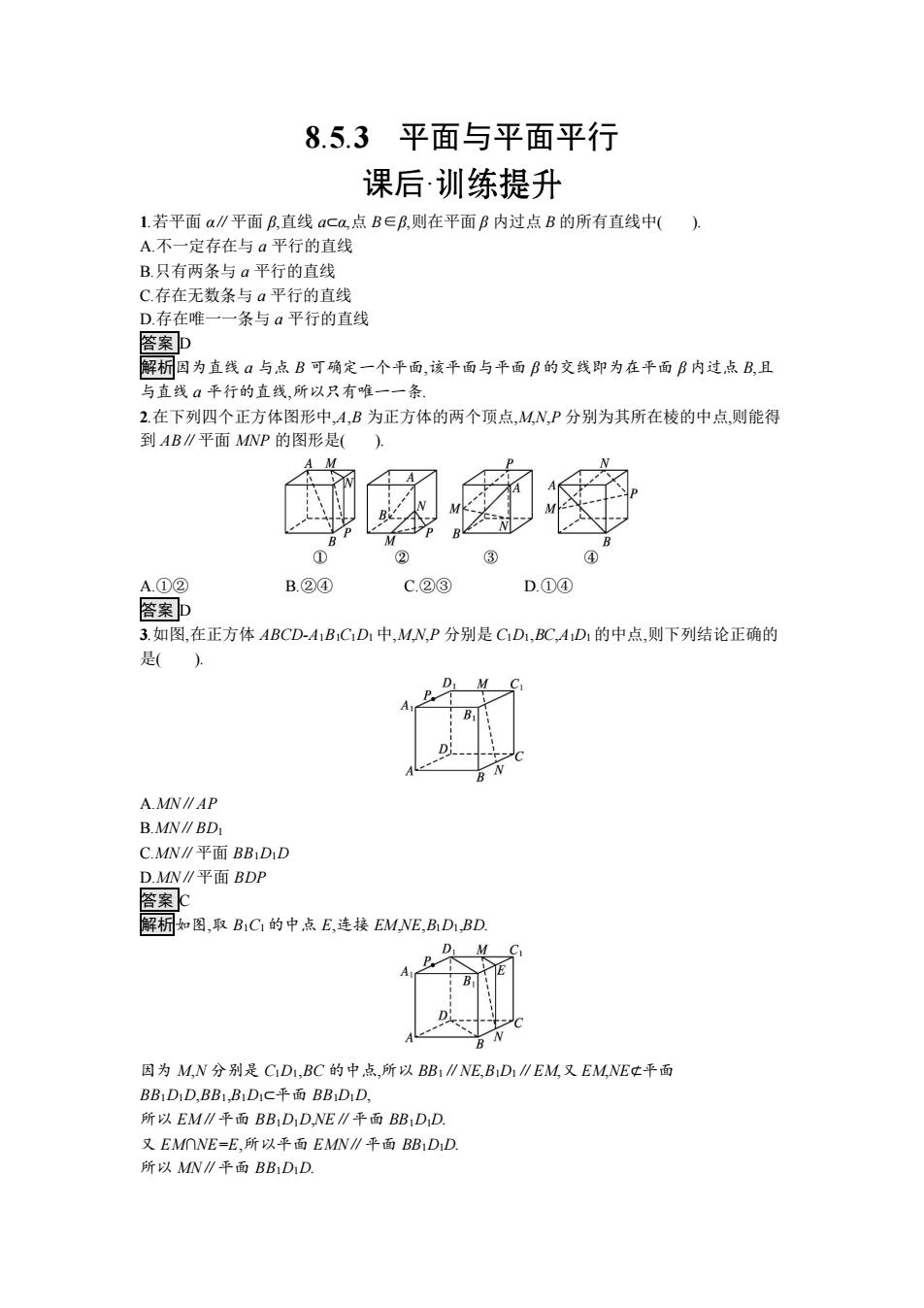
8.5.3 平面与平面平行 课后· 1.若平面 α∥平面 β,直线 a⊂α,点 B∈β,则在平面 β 内过点 B 的所有直线中( ). A.不一定存在与 a 平行的直线 B.只有两条与 a 平行的直线 C.存在无数条与 a 平行的直线 D.存在唯一一条与 a 平行的直线 答案 D 解析因为直线 a 与点 B 可确定一个平面,该平面与平面 β 的交线即为在平面 β 内过点 B,且 与直线 a 平行的直线,所以只有唯一一条. 2.在下列四个正方体图形中,A,B 为正方体的两个顶点,M,N,P 分别为其所在棱的中点,则能得 到 AB∥平面 MNP 的图形是( ). A.①② B.②④ C.②③ D.①④ 答案 D 3.如图,在正方体 ABCD-A1B1C1D1 中,M,N,P 分别是 C1D1,BC,A1D1 的中点,则下列结论正确的 是( ). A.MN∥AP B.MN∥BD1 C.MN∥平面 BB1D1D D.MN∥平面 BDP 答案 C 解析如图,取 B1C1 的中点 E,连接 EM,NE,B1D1,BD. 因为 M,N 分别是 C1D1,BC 的中点,所以 BB1∥NE,B1D1∥EM,又 EM,NE⊄平面 BB1D1D,BB1,B1D1⊂平面 BB1D1D, 所以 EM∥平面 BB1D1D,NE∥平面 BB1D1D. 又 EM∩NE=E,所以平面 EMN∥平面 BB1D1D. 所以 MN∥平面 BB1D1D

4.已知a,b,1是直线,a,B是平面,给出下列说法: ①若a∥b,aca,bcf,则a∥B: ②若a∥B,a与a相交,则a与B相交: ③若lca,mCa,且1∥B,m∥B,则a∥B: ④若a∥B,b∥a,且a∥B,则a∥b 其中说法错误的序号是」 答案①③④ 解析对于①,α,B可能相交,故①错误. 对于②假设a∥B或aCB,则由a∥B,知aCa或a∥a这与a与a相交矛盾,所以a与B相交, 故②正确 对于③当1∥m时,aB可能相交,故③错误 对于④a与b可能平行、相交或异面,故④错误 5.(多选题)一正方体的平面展开图如图所示,关于该正方体,下列说法正确的有(). A.BM∥平面ADNE B.CN∥平面ABFE C.平面BDM∥平面AFN D.平面BDE∥平面NCF 答案ABCD 解桐展开图可以折成正方体如图①所示。 图 图② 在正方体中,连接AN,如图②所示」 :AB∥MN,且AB=MNg ,:四边形ABMN是平行四边形 .:BMI∥AN,:BM∥平面ADNE. 同理可证CN∥平面ABFE,:A,B正确;
4.已知 a,b,l 是直线,α,β 是平面,给出下列说法: ①若 a∥b,a⊂α,b⊂β,则 α∥β; ②若 α∥β,a 与 α 相交,则 a 与 β 相交; ③若 l⊂α,m⊂α,且 l∥β,m∥β,则 α∥β; ④若 a∥β,b∥α,且 α∥β,则 a∥b. 其中说法错误的序号是 . 答案①③④ 解析对于①,α,β 可能相交,故①错误. 对于②,假设 a∥β 或 a⊂β,则由 α∥β,知 a⊂α 或 a∥α,这与 a 与 α 相交矛盾,所以 a 与 β 相交, 故②正确. 对于③,当 l∥m 时,α,β 可能相交,故③错误. 对于④,a 与 b 可能平行、相交或异面,故④错误. 5.(多选题)一正方体的平面展开图如图所示,关于该正方体,下列说法正确的有( ). A.BM∥平面 ADNE B.CN∥平面 ABFE C.平面 BDM∥平面 AFN D.平面 BDE∥平面 NCF 答案 ABCD 解析展开图可以折成正方体如图①所示. 图① 图② 在正方体中,连接 AN,如图②所示. ∵AB∥MN,且 AB=MN, ∴四边形 ABMN 是平行四边形. ∴BM∥AN.∴BM∥平面 ADNE. 同理可证 CN∥平面 ABFE,∴A,B 正确;

图③ 如图③在图②的基础上,连接NF,BE,BD,DM,CF,可以证明BM∥平面AFN,BD∥平面AFN,则 平面BDM∥平面AFN同理可证平面BDE∥平面NCF所以C.D正确」 6.如图,平面a过正方体ABCD-A1B1C1D1的三个顶点B,D,A,且a与底面A1B1C1D1的交线为 I,则I与BD1的位置关系是 B 管案平行 解析因为DD1∥BB1,DD1=BB1, 所以四边形BDD1B1是平行四边形. 所以BD∥B1D1. 又B1D1C平面A1B1C1D1,BDt平面A1B1CD1, 所以BD∥平面A1B1CD1. 又BDCa,an平面A1B1C1D1=l, 所以1∥BD.所以I∥B1D1. 7.如图,在正方体ABCD-A1B1CD1中,E,F,G,H分别为棱CC,CD1,D1D,CD的中点,N是BC的 中点,点M在四边形EFGH及其内部运动,则M满足 时,有MN∥平面B1BDD1. 0 答案点M在FH上 解析连接FH,FN(图略), :F,H分别是棱C1D,CD的中点 :FH∥DD1 :FHt平面B1BDD1,DD1C平面B1BDD1, :FH∥平面B1BDD1. 同理,N∥平面B1BDD1 又FHOHN=H, ,:平面FHN∥平面B1BDD1, 又平面FHNn平面EFGH=FH, .:当M∈FH时,MNc平面FHN
图③ 如图③,在图②的基础上,连接 NF,BE,BD,DM,CF,可以证明 BM∥平面 AFN,BD∥平面 AFN,则 平面 BDM∥平面 AFN,同理可证平面 BDE∥平面 NCF,所以 C,D 正确. 6.如图,平面 α 过正方体 ABCD-A1B1C1D1 的三个顶点 B,D,A1,且 α 与底面 A1B1C1D1 的交线为 l,则 l 与 B1D1 的位置关系是 . 答案平行 解析因为 DD1∥BB1,DD1=BB1, 所以四边形 BDD1B1 是平行四边形. 所以 BD∥B1D1. 又 B1D1⊂平面 A1B1C1D1,BD⊄平面 A1B1C1D1, 所以 BD∥平面 A1B1C1D1. 又 BD⊂α,α∩平面 A1B1C1D1=l, 所以 l∥BD.所以 l∥B1D1. 7.如图,在正方体 ABCD-A1B1C1D1 中,E,F,G,H 分别为棱 CC1,C1D1,D1D,CD 的中点,N 是 BC 的 中点,点 M 在四边形 EFGH 及其内部运动,则 M 满足 时,有 MN∥平面 B1BDD1. 答案点 M 在 FH 上 解析连接 FH,FN(图略), ∵F,H 分别是棱 C1D1,CD 的中点, ∴FH∥DD1. ∵FH⊄平面 B1BDD1,DD1⊂平面 B1BDD1, ∴FH∥平面 B1BDD1. 同理,HN∥平面 B1BDD1. 又 FH∩HN=H, ∴平面 FHN∥平面 B1BDD1, 又平面 FHN∩平面 EFGH=FH, ∴当 M∈FH 时,MN⊂平面 FHN
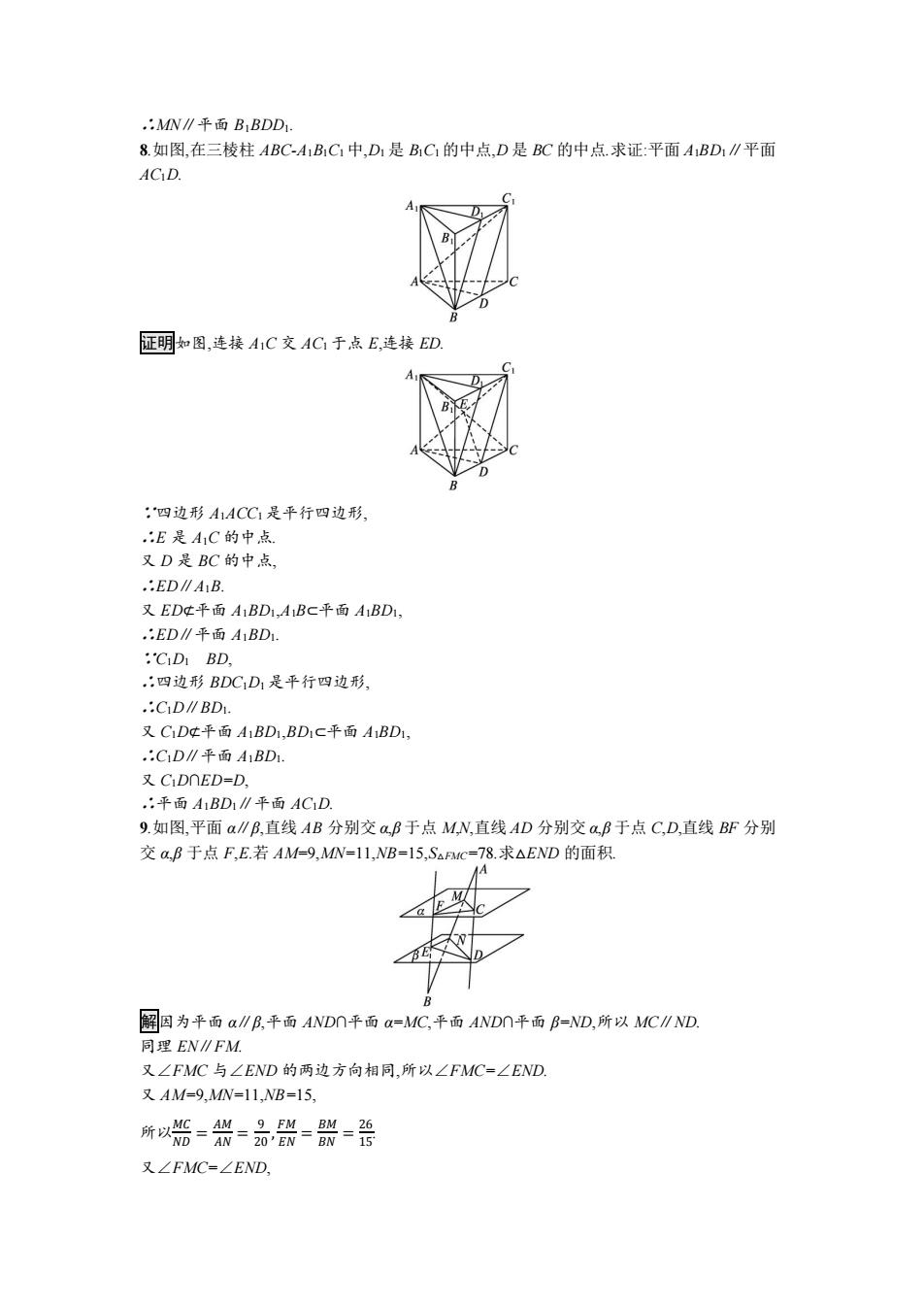
,MN∥平面B1BDD1 8.如图,在三棱柱ABC-A1B1C中,D1是B1C的中点,D是BC的中点.求证:平面A1BD1∥平面 ACD. 证明如图,连接A1C交AC于点E,连接ED, :四边形A1ACC1是平行四边形 .:E是A1C的中点 又D是BC的中点, .:ED∥A1B. 又EDt平面A1BD1,ABC平面A1BD1, .:ED∥平面A1BD1. :'CiD BD, :四边形BDCD1是平行四边形, .:CD∥BD. 又C1Dt平面A1BD1,BD1C平面A1BD1, ,C1D∥平面A1BD1: 又C1DnED=D. .:平面A1BD1∥平面AC1D 9.如图,平面a∥B,直线AB分别交a,B于点M,N,直线AD分别交a,B于点C,D,直线BF分别 交a,B于点F,E.若AM=9,MN=11,NB=15,SaFc=78.求△END的面积 解国为平面a,∥B,平面ANDn平面a=MC,平面ANDn平面B=ND,所以MC∥ND, 同理EN∥FM 又∠FMC与∠END的两边方向相同,所以∠FMC=∠END. 又AM=9,MN=11,NB=15, 所以荒=兴=品器=器=兽 又∠FMC=∠END
∴MN∥平面 B1BDD1. 8.如图,在三棱柱 ABC-A1B1C1 中,D1 是 B1C1 的中点,D 是 BC 的中点.求证:平面 A1BD1∥平面 AC1D. 证明如图,连接 A1C 交 AC1 于点 E,连接 ED. ∵四边形 A1ACC1 是平行四边形, ∴E 是 A1C 的中点. 又 D 是 BC 的中点, ∴ED∥A1B. 又 ED⊄平面 A1BD1,A1B⊂平面 A1BD1, ∴ED∥平面 A1BD1. ∵C1D1 BD, ∴四边形 BDC1D1 是平行四边形, ∴C1D∥BD1. 又 C1D⊄平面 A1BD1,BD1⊂平面 A1BD1, ∴C1D∥平面 A1BD1. 又 C1D∩ED=D, ∴平面 A1BD1∥平面 AC1D. 9.如图,平面 α∥β,直线 AB 分别交 α,β 于点 M,N,直线 AD 分别交 α,β 于点 C,D,直线 BF 分别 交 α,β 于点 F,E.若 AM=9,MN=11,NB=15,S△FMC=78.求△END 的面积. 解因为平面 α∥β,平面 AND∩平面 α=MC,平面 AND∩平面 β=ND,所以 MC∥ND. 同理 EN∥FM. 又∠FMC 与∠END 的两边方向相同,所以∠FMC=∠END. 又 AM=9,MN=11,NB=15, 所以𝑀𝐶 𝑁𝐷 = 𝐴𝑀 𝐴𝑁 = 9 20 , 𝐹𝑀 𝐸𝑁 = 𝐵𝑀 𝐵𝑁 = 26 15. 又∠FMC=∠END

所以Awc FM-MC-sin∠FMC SAEND EN-ND-sinEND 50 又SAFMC=78,所以SAEND=100 故△END的面积为100. 10.如图@在直角梯形ABCP中,4P∥BC,AP⊥AB,AB=BC=AP,D为AP的中点,E,F,G分别 为PC,PD,CB的中点,将△PCD沿CD折起,得到四棱锥P-ABCD,如图②所示. 图① 图② 求证:在四棱锥P-ABCD中,AP∥平面EFG. 证明在四棱锥P-ABCD中, :E,F分别为PC,PD的中点, .EF∥CD :AB∥CD, .:EF∥AB. ·EF¢平面PAB,ABC平面PAB .:EF∥平面PAB 同理EG∥平面PAB. 又EFNEG=E,EFc平面EFG,EGc平面EFG, .:平面EFG∥平面PAB. :APC平面PAB, .AP∥平面EFG
所以 𝑆△𝐹𝑀𝐶 𝑆△𝐸𝑁𝐷 = 1 2 𝐹𝑀·𝑀𝐶·sin∠𝐹𝑀𝐶 1 2 𝐸𝑁·𝑁𝐷·sin∠𝐸𝑁𝐷 = 26 15 × 9 20 = 39 50. 又 S△FMC=78,所以 S△END=100. 故△END 的面积为 100. 10.如图①,在直角梯形 ABCP 中,AP∥BC,AP⊥AB,AB=BC=1 2 AP,D 为 AP 的中点,E,F,G 分别 为 PC,PD,CB 的中点,将△PCD 沿 CD 折起,得到四棱锥 P-ABCD,如图②所示. 图① 图② 求证:在四棱锥 P-ABCD 中,AP∥平面 EFG. 证明在四棱锥 P-ABCD 中, ∵E,F 分别为 PC,PD 的中点, ∴EF∥CD. ∵AB∥CD, ∴EF∥AB. ∵EF⊄平面 PAB,AB⊂平面 PAB, ∴EF∥平面 PAB. 同理 EG∥平面 PAB. 又 EF∩EG=E,EF⊂平面 EFG,EG⊂平面 EFG, ∴平面 EFG∥平面 PAB. ∵AP⊂平面 PAB, ∴AP∥平面 EFG