8.5.1直线与直线平行 课后·训练提升 1.己知a,b,c,d均为直线,且a∥b,b∥c,c∥d,则a与d的位置关系是() A平行 B.相交 C.异面 D.不确定 答案A 解析:a∥b,b∥c,:a∥c.又c∥d,:a∥d 2.如图,在正方体ABCD-A1B1CD1中,直线Ic平面A1B1CD1,且直线I与直线B1C不平行,则 下列关系一定不可能成立的是(). A.1与AD平行 B.I与AD不平行 C.I与AC平行 D.I与BD平行 答案A 解析假设I∥AD,则由AD∥BC∥B1C1,知1∥BC,这与直线1与直线B1C1不平行矛盾,所以直 线1与直线AD不平行. 3.如图,在三棱柱ABC-A1B1C1中,E,F分别是AB,AC上的点,且AE:EB=AF:FC,则EF与 B1C1的位置关系是 答案平行 解析在△ABC中, 因为AE,EB=AFFC所以EF∥BC. 又在三棱柱ABC-A1B1C中,BC∥B1C1, 所以EF∥B1C. 4.如图,已知E,F分别是长方体ABCD-A1B1C1D1的棱AA1和棱CC1上的点,且AE=C1F,求证: 四边形EBFD1是平行四边形 证明如图,在DD1上取DM=AE,连接CM,EM
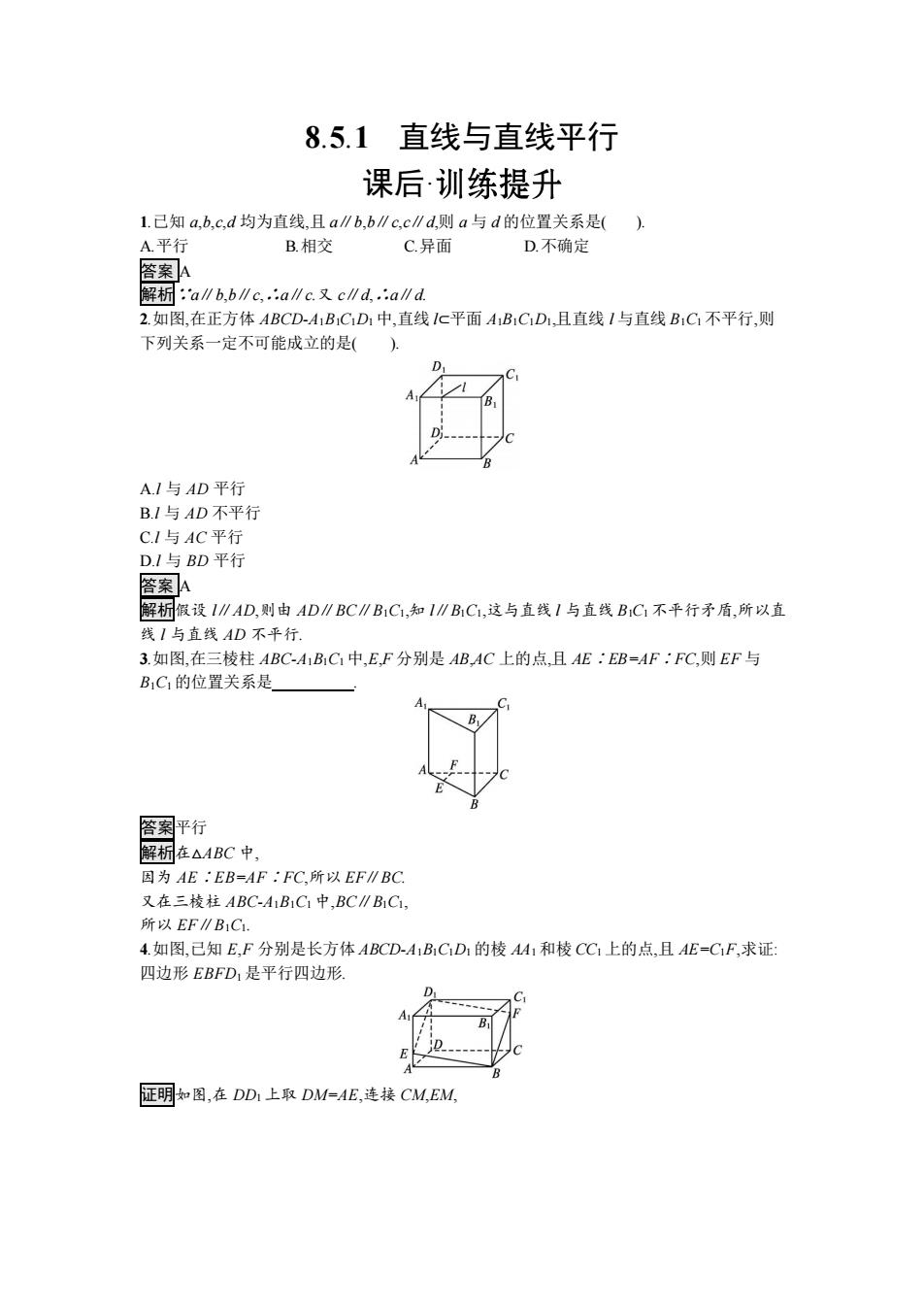
8.5.1 直线与直线平行 课后· 1.已知 a,b,c,d 均为直线,且 a∥b,b∥c,c∥d,则 a 与 d 的位置关系是( ). A.平行 B.相交 C.异面 D.不确定 答案 A 解析∵a∥b,b∥c,∴a∥c.又 c∥d,∴a∥d. 2.如图,在正方体 ABCD-A1B1C1D1 中,直线 l⊂平面 A1B1C1D1,且直线 l 与直线 B1C1 不平行,则 下列关系一定不可能成立的是( ). A.l 与 AD 平行 B.l 与 AD 不平行 C.l 与 AC 平行 D.l 与 BD 平行 答案 A 解析假设 l∥AD,则由 AD∥BC∥B1C1,知 l∥B1C1,这与直线 l 与直线 B1C1 不平行矛盾,所以直 线 l 与直线 AD 不平行. 3.如图,在三棱柱 ABC-A1B1C1 中,E,F 分别是 AB,AC 上的点,且 AE∶EB=AF∶FC,则 EF 与 B1C1 的位置关系是 . 答案平行 解析在△ABC 中, 因为 AE∶EB=AF∶FC,所以 EF∥BC. 又在三棱柱 ABC-A1B1C1 中,BC∥B1C1, 所以 EF∥B1C1. 4.如图,已知 E,F 分别是长方体 ABCD-A1B1C1D1 的棱 AA1 和棱 CC1 上的点,且 AE=C1F,求证: 四边形 EBFD1 是平行四边形. 证明如图,在 DD1 上取 DM=AE,连接 CM,EM

因为AA1∥DD1,所以四边形ADME是平行四边形,所以EM AD 又ADBC,所以EMBC 所以四边形BCME是平行四边形,所以BECM. 同理CMDF 所以BEDF, 所以四边形EBFD1是平行四边形. 5.如图,在平行六面体ABCD-A1B1CD1中,M,N,P分别是CC,B1C1,CD1的中点. 求证:∠NMP=∠BA1D. 证明如图,连接CB1,CD1. .'CD A1B1, :四边形A1B1CD是平行四边形, .A1D∥B1C :M,N分别是CC,B1C1的中点, .:MN∥B1C .:MN∥AD 同理,MP∥BA. :∠NMP与∠BA1D的两边分别平行且方向相反, .:∠NMP=∠BA1D 6.如图,P是△ABC所在平面外一点,D,E分别是△PAB,△PBC的重心 求证:DE∥AC,且DE-AC 证明如图,连接PD,PE并延长,分别交AB于点G,交BC于点H,则G,H分别是AB,BC的中点, 连接GH,则GH∥AC,且GH之AC
因为 AA1∥DD1,所以四边形 ADME 是平行四边形,所以 EM AD. 又 AD BC,所以 EM BC, 所以四边形 BCME 是平行四边形,所以 BE CM. 同理 CM D1F. 所以 BE D1F, 所以四边形 EBFD1 是平行四边形. 5.如图,在平行六面体 ABCD-A1B1C1D1 中,M,N,P 分别是 CC1,B1C1,C1D1 的中点. 求证:∠NMP=∠BA1D. 证明如图,连接 CB1,CD1. ∵CD A1B1, ∴四边形 A1B1CD 是平行四边形, ∴A1D∥B1C. ∵M,N 分别是 CC1,B1C1 的中点, ∴MN∥B1C. ∴MN∥A1D. 同理,MP∥BA1. ∴∠NMP 与∠BA1D 的两边分别平行且方向相反, ∴∠NMP=∠BA1D. 6.如图,P 是△ABC 所在平面外一点,D,E 分别是△PAB,△PBC 的重心. 求证:DE∥AC,且 DE=1 3 AC. 证明如图,连接 PD,PE 并延长,分别交 AB 于点 G,交 BC 于点 H,则 G,H 分别是 AB,BC 的中点, 连接 GH,则 GH∥AC,且 GH=1 2 AC

G氏 在△PHG中,由题意可知E PD PG =号所以DE∥GH且DEGH所以DEIAC,.且DE-AC E 7.如图,四边形ABED为正方形,四边形EFGD与四边形ADGC均为直角梯形,AC∥DG∥ EF,DA=DE=DG,AC=EF-DG.求证:BF∥CG, M 证明如图,取DG的中点M,连接AMFM :EF∥DG,EF-DG, .:EF∥DM,EF=DM :四边形EFMD为平行四边形, .:FM∥ED,FM=ED. :四边形ABED为正方形, .:AB∥FM,AB=FM ,:四边形ABFM为平行四边形, .:AMI∥BF :'AC-DG.MG-DG.AC//DG. :四边形ACGM为平行四边形, .:AM∥CG. .:BF∥CG
在△PHG 中,由题意可知𝑃𝐸 𝑃𝐻 = 𝑃𝐷 𝑃𝐺 = 2 3 ,所以 DE∥GH,且 DE=2 3 GH.所以 DE∥AC,且 DE=1 3 AC. 7.如图,四边形 ABED 为正方形,四边形 EFGD 与四边形 ADGC 均为直角梯形,AC∥DG∥ EF,DA=DE=DG,AC=EF=1 2 DG.求证:BF∥CG. 证明如图,取 DG 的中点 M,连接 AM,FM, ∵EF∥DG,EF=1 2 DG, ∴EF∥DM,EF=DM, ∴四边形 EFMD 为平行四边形, ∴FM∥ED,FM=ED. ∵四边形 ABED 为正方形, ∴AB∥FM,AB=FM, ∴四边形 ABFM 为平行四边形, ∴AM∥BF. ∵AC=1 2 DG,MG=1 2 DG,AC∥DG, ∴四边形 ACGM 为平行四边形, ∴AM∥CG. ∴BF∥CG