
8.42空间点、直线、平面之间的位置关系 课后·训练提升 1.(多选题)a,b是直线,a是平面,则下列结论正确的是( A.若a∥a,bca,则a∥b B.若aca,bta则a,b无公共点 C.若ata,则a∥a或a与a相交 D.若ana=A,则ata 答案cD 解桐结合直线与平面的位置关系可知,AB错误,CD正确. 2.下列说法中,正确的个数是() ①空间中没有交点的两条直线是平行直线: ②若一条直线和两条平行直线中的一条相交,则它和另一条也相交 ③若直线a在平面a外,则a∥ ④分别在两个平面内的两条直线不是相交直线, A.0 B.1 C.2 D.3 答案A 解析①中,两条直线也可能异面,故①错误;②中,两条直线也可能异面,故②错误;③冲,á也可 能与平面α相交,故③错误;④中,两条直线也可能是相交直线,故①错误. 3.经过平面外两点与这个平面平行的平面() A只有一个 B.至少有一个 C.可能不存在 D.有无数个 含案c 解析当这两点的连线与平面相交时,不存在平面与这个平面平行;当这两点的连线与平面平 行时,有且只有一个平面与这个平面平行 4.(多选题)下列结论正确的是(). A.三个平面最多可以把空间分成八部分 B.若直线ac平面a,直线bc平面B,则a与b相交”与“a与B相交等价 C.若anf=l,直线ac平面a,直线bc平面B,且a∩nb=P,则P∈I D.若n条直线中任意两条共面,则它们共面 答案AC 解析A正确;对于B,由“a与B相交”推不出“a与b相交”,故B错误:C正确;对于D,例如四棱 柱的任意两条侧棱都共面,但这4条侧棱并不共面,故D错误 所以正确的是AC 5.己知两条相交直线a,b都在平面a内且都不在平面B内,平面a与B相交,则a与b(). A.一定与平面B都相交 B.至少有一条与平面B相交 C.至多有一条与平面B相交 D.可能与平面B都不相交 答案B
8.4.2 空间点、直线、平面之间的位置关系 课后· 1.(多选题)a,b 是直线,α 是平面,则下列结论正确的是( ). A.若 a∥α,b⊂α,则 a∥b B.若 a⊂α,b⊄α,则 a,b 无公共点 C.若 a⊄α,则 a∥α 或 a 与 α 相交 D.若 a∩α=A,则 a⊄α 答案 CD 解析结合直线与平面的位置关系可知,AB 错误,CD 正确. 2.下列说法中,正确的个数是( ). ①空间中没有交点的两条直线是平行直线; ②若一条直线和两条平行直线中的一条相交,则它和另一条也相交; ③若直线 a 在平面 α 外,则 a∥α; ④分别在两个平面内的两条直线不是相交直线. A.0 B.1 C.2 D.3 答案 A 解析①中,两条直线也可能异面,故①错误;②中,两条直线也可能异面,故②错误;③中,a 也可 能与平面 α 相交,故③错误;④中,两条直线也可能是相交直线,故④错误. 3.经过平面外两点与这个平面平行的平面( ). A.只有一个 B.至少有一个 C.可能不存在 D.有无数个 答案 C 解析当这两点的连线与平面相交时,不存在平面与这个平面平行;当这两点的连线与平面平 行时,有且只有一个平面与这个平面平行. 4.(多选题)下列结论正确的是( ). A.三个平面最多可以把空间分成八部分 B.若直线 a⊂平面 α,直线 b⊂平面 β,则“a 与 b 相交”与“α 与 β 相交”等价 C.若 α∩β=l,直线 a⊂平面 α,直线 b⊂平面 β,且 a∩b=P,则 P∈l D.若 n 条直线中任意两条共面,则它们共面 答案 AC 解析 A 正确;对于 B,由“α 与 β 相交”推不出“a 与 b 相交”,故 B 错误;C 正确;对于 D,例如四棱 柱的任意两条侧棱都共面,但这 4 条侧棱并不共面,故 D 错误. 所以正确的是 AC. 5.已知两条相交直线 a,b 都在平面 α 内且都不在平面 β 内,平面 α 与 β 相交,则 a 与 b( ). A.一定与平面 β 都相交 B.至少有一条与平面 β 相交 C.至多有一条与平面 β 相交 D.可能与平面 β 都不相交 答案 B
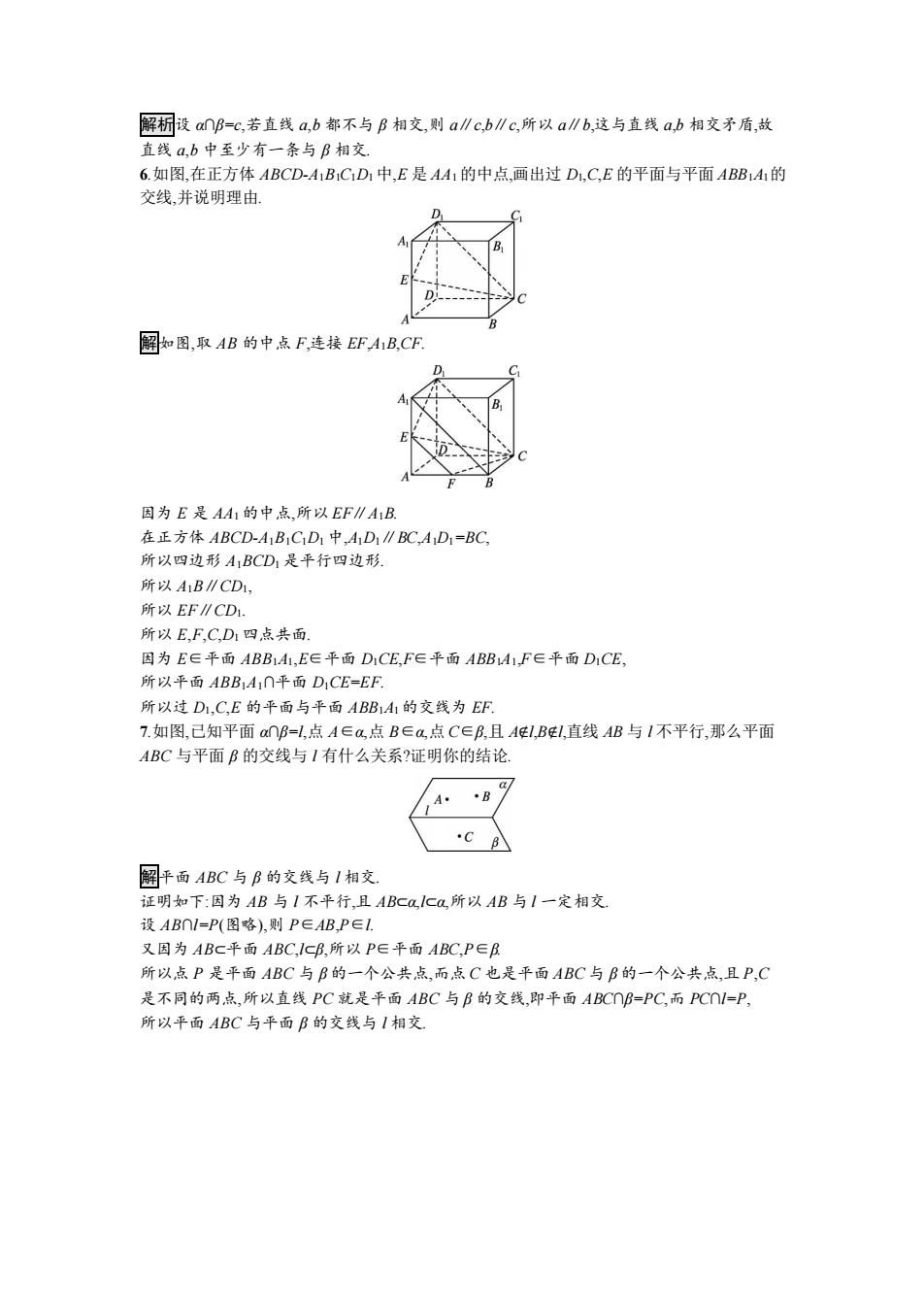
解标设anB=c,若直线a,b都不与B相交,则a∥c,b∥c,所以a∥b,这与直线a,b相交矛盾,故 直线a,b中至少有一条与B相交. 6.如图,在正方体ABCD-A1B1CD1中,E是AA1的中点,画出过D1,C,E的平面与平面ABB1A的 交线,并说明理由 解如图,取AB的中点F,连接EFAB,CF 因为E是AA1的中点,所以EF∥A1B 在正方体ABCD-A1B1C1D1中,A1D1∥BC,AD1=BC, 所以四边形A1BCD1是平行四边形. 所以AB∥CD1, 所以EF∥CD1. 所以E,F,C,D1四点共面 因为E∈平面ABB1A1,E∈平面DCE,F∈平面ABB1A1,F∈平面D1CE, 所以平面ABBA,∩平面D1CE=EF 所以过D1,C,E的平面与平面ABB1A1的交线为EF 7.如图,己知平面∩B=l,点A∈a,点B∈a,点C∈B,且AEI,BI,直线AB与I不平行,那么平面 ABC与平面B的交线与I有什么关系?证明你的结论, 解平面ABC与B的交线与1相交 证明如下:因为AB与I不平行,且ABCa,ICa,所以AB与I一定相交. 设AB∩I=P(图略),则P∈AB,P∈I 又因为ABC平面ABC,ICB,所以P∈平面ABC,P∈B 所以点P是平面ABC与B的一个公共点,而点C也是平面ABC与B的一个公共点,且P,C 是不同的两,点,所以直线PC就是平面ABC与B的交线,即平面ABC∩B=PC,而PC∩=P, 所以平面ABC与平面B的交线与1相交
解析设 α∩β=c,若直线 a,b 都不与 β 相交,则 a∥c,b∥c,所以 a∥b,这与直线 a,b 相交矛盾,故 直线 a,b 中至少有一条与 β 相交. 6.如图,在正方体 ABCD-A1B1C1D1 中,E 是 AA1 的中点,画出过 D1,C,E 的平面与平面 ABB1A1的 交线,并说明理由. 解如图,取 AB 的中点 F,连接 EF,A1B,CF. 因为 E 是 AA1 的中点,所以 EF∥A1B. 在正方体 ABCD-A1B1C1D1 中,A1D1∥BC,A1D1=BC, 所以四边形 A1BCD1 是平行四边形. 所以 A1B∥CD1, 所以 EF∥CD1. 所以 E,F,C,D1 四点共面. 因为 E∈平面 ABB1A1,E∈平面 D1CE,F∈平面 ABB1A1,F∈平面 D1CE, 所以平面 ABB1A1∩平面 D1CE=EF. 所以过 D1,C,E 的平面与平面 ABB1A1 的交线为 EF. 7.如图,已知平面 α∩β=l,点 A∈α,点 B∈α,点 C∈β,且 A∉l,B∉l,直线 AB 与 l 不平行,那么平面 ABC 与平面 β 的交线与 l 有什么关系?证明你的结论. 解平面 ABC 与 β 的交线与 l 相交. 证明如下:因为 AB 与 l 不平行,且 AB⊂α,l⊂α,所以 AB 与 l 一定相交. 设 AB∩l=P(图略),则 P∈AB,P∈l. 又因为 AB⊂平面 ABC,l⊂β,所以 P∈平面 ABC,P∈β. 所以点 P 是平面 ABC 与 β 的一个公共点,而点 C 也是平面 ABC 与 β 的一个公共点,且 P,C 是不同的两点,所以直线 PC 就是平面 ABC 与 β 的交线,即平面 ABC∩β=PC,而 PC∩l=P, 所以平面 ABC 与平面 β 的交线与 l 相交