8.5.2直线与平面平行 课后·训练提升 1.(多选题)下列说法错误的是() A.一条直线和另一条直线平行,那么它和经过另一条直线的任何平面平行 B.一条直线平行于一个平面,则这条直线与这个平面内所有直线都没有公共点,因此这条直线 与这个平面内的所有直线都平行 C.若直线1与平面a不平行,则1与a内任一直线都不平行 D.与一平面内无数条直线都平行的直线必与此平面平行 答案ABCD 2.如图,在正方体ABCD-A1B1CD1中,已知E,F,G分别是线段41C1上的点,且 A1E=EF=FG=GC.则下列直线与平面A1BD平行的是(). D D A.CE B.CF C.CG D.CC 答案B 解析如图,连接AC交BD于点O,连接41O,CF D 在正方体ABCD-A1B1C1D1中, AC AC.A F-74CL.OC-AC,.AF OC. :四边形A1OCF是平行四边形,:A1O∥CF 又A1OC平面A1BD,CFt平面ABD, ,:CF∥平面A1BD 3.如图,在三棱柱ABC-A1B1C1中,过A1B的平面与平面ABC交于直线DE,则直线DE与直线 AB的位置关系是() A.异面 B.平行 C.相交
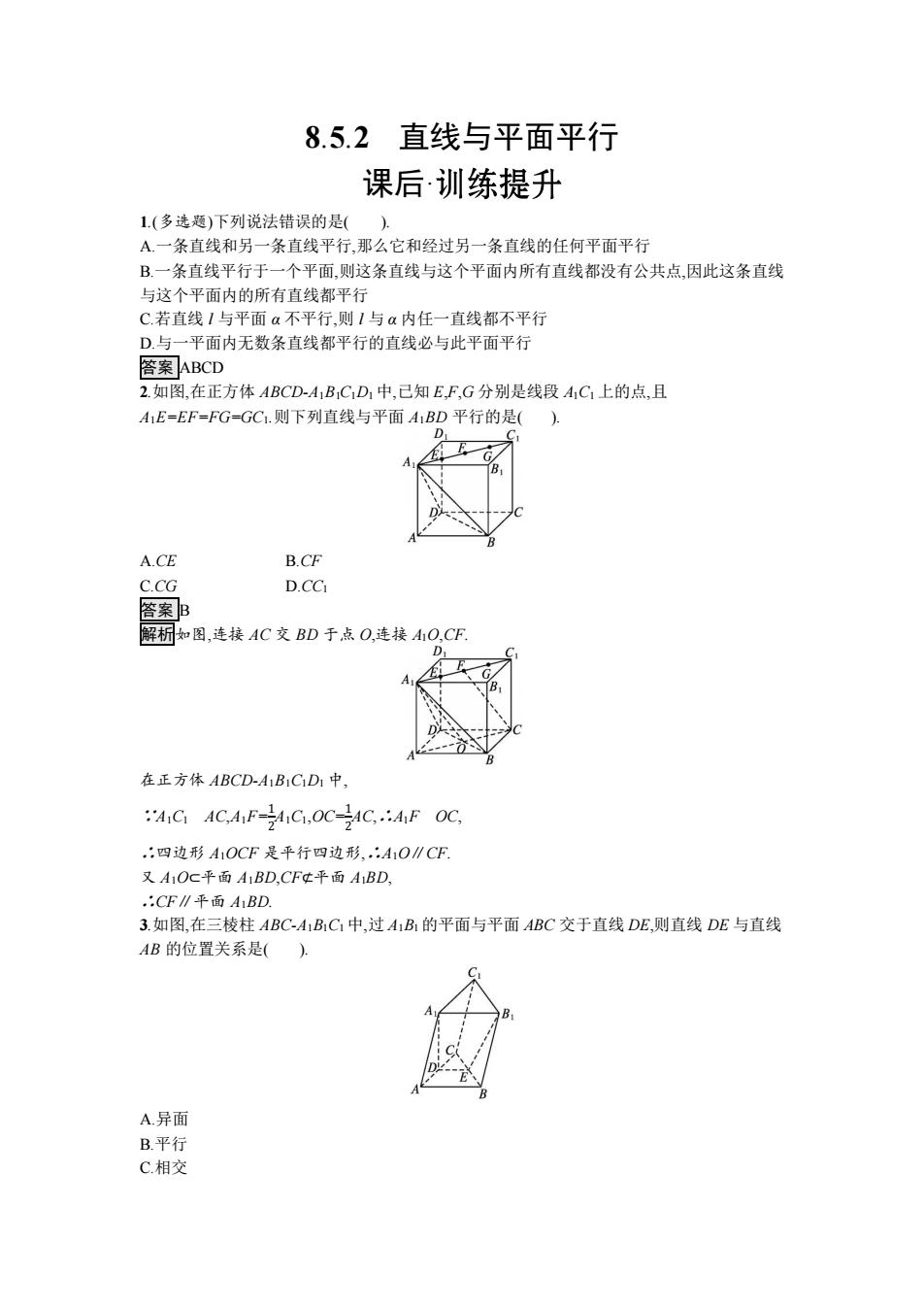
8.5.2 直线与平面平行 课后· 1.(多选题)下列说法错误的是( ). A.一条直线和另一条直线平行,那么它和经过另一条直线的任何平面平行 B.一条直线平行于一个平面,则这条直线与这个平面内所有直线都没有公共点,因此这条直线 与这个平面内的所有直线都平行 C.若直线 l 与平面 α 不平行,则 l 与 α 内任一直线都不平行 D.与一平面内无数条直线都平行的直线必与此平面平行 答案 ABCD 2.如图,在正方体 ABCD-A1B1C1D1 中,已知 E,F,G 分别是线段 A1C1 上的点,且 A1E=EF=FG=GC1.则下列直线与平面 A1BD 平行的是( ). A.CE B.CF C.CG D.CC1 答案 B 解析如图,连接 AC 交 BD 于点 O,连接 A1O,CF. 在正方体 ABCD-A1B1C1D1 中, ∵A1C1 AC,A1F=1 2 A1C1,OC=1 2 AC,∴A1F OC, ∴四边形 A1OCF 是平行四边形,∴A1O∥CF. 又 A1O⊂平面 A1BD,CF⊄平面 A1BD, ∴CF∥平面 A1BD. 3.如图,在三棱柱 ABC-A1B1C1 中,过 A1B1 的平面与平面 ABC 交于直线 DE,则直线 DE 与直线 AB 的位置关系是( ). A.异面 B.平行 C.相交

D以上均有可能 答案B 解析因为A1B1∥AB,ABC平面ABC,A1B1平面ABC,所以AB1∥平面ABC. 又A1B1C平面A1B1ED,平面AB1EDn平面ABC=DE,所以DE∥AB1. 又AB∥A1B1,所以DE∥AB 4.如图,四棱锥S-ABCD的所有的棱长都等于2,E是SA的中点,过C,D,E三点的平面与SB交 于点F,则四边形DEFC的周长为() A.2+V3 B.3+v3 C.3+2V3 D.2+2v3 答案 解析由AB=BC=CD=DA=2,得AB∥CD,则有AB∥平面DCFE, :·平面SABn平面DCFE=EF,:AB∥EF :E是SA的中点,:F是SB的中点, ..EF=1.DE=CF=V3. .:四边形DEFC的周长为3+2V3. 5.如图,a∥a,点A在a的另一侧,B,C,D∈a,线段AB,ACAD分别交a于点E,F,G,若 BD=4.CF=4.AF=5,则EG= 靥案鹘 解标因为a∥a,an平面ABD=EG, 所以a∥EG,即BD∥EG,所以先=品 即克=华所以G号 4 9 6.如图,在三棱柱ABC-A1B1C1中,D为BC的中点,连接AD,DC1,A1B,AC1. 求证:A1B∥平面ADC1. 证明如图,连接A1C交AC于点O,连接OD
D.以上均有可能 答案 B 解析因为 A1B1∥AB,AB⊂平面 ABC,A1B1⊄平面 ABC,所以 A1B1∥平面 ABC. 又 A1B1⊂平面 A1B1ED,平面 A1B1ED∩平面 ABC=DE,所以 DE∥A1B1. 又 AB∥A1B1,所以 DE∥AB. 4.如图,四棱锥 S-ABCD 的所有的棱长都等于 2,E 是 SA 的中点,过 C,D,E 三点的平面与 SB 交 于点 F,则四边形 DEFC 的周长为( ). A.2+√3 B.3+√3 C.3+2√3 D.2+2√3 答案 C 解析由 AB=BC=CD=DA=2,得 AB∥CD,则有 AB∥平面 DCFE, ∵平面 SAB∩平面 DCFE=EF,∴AB∥EF. ∵E 是 SA 的中点,∴F 是 SB 的中点, ∴EF=1,DE=CF=√3. ∴四边形 DEFC 的周长为 3+2√3. 5.如图,a∥α,点 A 在 α 的另一侧,B,C,D∈a,线段 AB,AC,AD 分别交 α 于点 E,F,G,若 BD=4,CF=4,AF=5,则 EG= . 答案20 9 解析因为 a∥α,α∩平面 ABD=EG, 所以 a∥EG,即 BD∥EG,所以𝐴𝐹 𝐴𝐶 = 𝐸𝐺 𝐵𝐷, 即 5 4+5 = 𝐸𝐺 4 ,所以 EG=20 9 . 6.如图,在三棱柱 ABC-A1B1C1 中,D 为 BC 的中点,连接 AD,DC1,A1B,AC1. 求证:A1B∥平面 ADC1. 证明如图,连接 A1C 交 AC1 于点 O,连接 OD
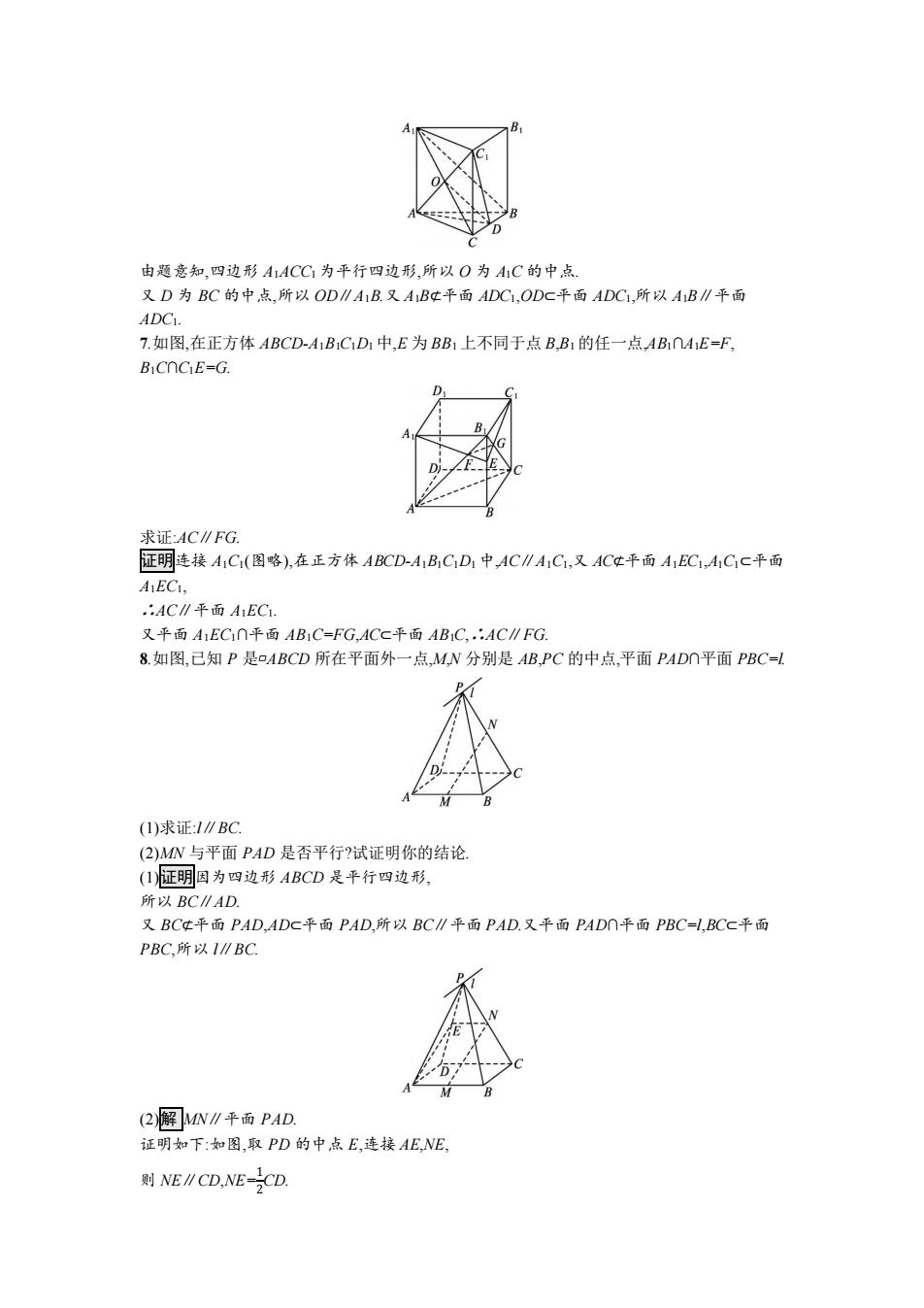
由题意知,四边形A1ACC为平行四边形,所以O为1C的中点. 又D为BC的中点,所以OD∥A1B.又ABt平面ADC1,ODC平面ADC1,所以A1B∥平面 ADC1. 7.如图,在正方体ABCD-A1B1CD1中,E为BB1上不同于点B,B1的任一点AB∩4E=F, BICOCIE=G. D 求证:AC∥FG. 证明连接A1C(图略),在正方体ABCD-A1B1C,D1中,AC∥A1C,又ACt平面A1EC1,A1C1c平面 A1EC1, .AC∥平面A1EC. 又平面A1EC∩平面AB1C=FG,ACC平面AB1C,:AC∥FG 8.如图,已知P是ABCD所在平面外一点,M,N分别是AB,PC的中点,平面PADn平面PBC=l (1)求证:l∥BC (2)MN与平面PAD是否平行?试证明你的结论, (I证明因为四边形ABCD是平行四边形, 所以BC∥AD 又BCt平面PAD,ADC平面PAD,所以BC∥平面PAD.又平面PADn平面PBC=I,BCC平面 PBC,所以I∥BC (2解MN∥平面PAD, 证明如下:如图,取PD的中,点E,连接AE,NE, 则NE∥CD,NECD
由题意知,四边形 A1ACC1 为平行四边形,所以 O 为 A1C 的中点. 又 D 为 BC 的中点,所以 OD∥A1B.又 A1B⊄平面 ADC1,OD⊂平面 ADC1,所以 A1B∥平面 ADC1. 7.如图,在正方体 ABCD-A1B1C1D1 中,E 为 BB1 上不同于点 B,B1 的任一点,AB1∩A1E=F, B1C∩C1E=G. 求证:AC∥FG. 证明连接 A1C1(图略),在正方体 ABCD-A1B1C1D1 中,AC∥A1C1,又 AC⊄平面 A1EC1,A1C1⊂平面 A1EC1, ∴AC∥平面 A1EC1. 又平面 A1EC1∩平面 AB1C=FG,AC⊂平面 AB1C,∴AC∥FG. 8.如图,已知 P 是▱ABCD 所在平面外一点,M,N 分别是 AB,PC 的中点,平面 PAD∩平面 PBC=l. (1)求证:l∥BC. (2)MN 与平面 PAD 是否平行?试证明你的结论. (1)证明因为四边形 ABCD 是平行四边形, 所以 BC∥AD. 又 BC⊄平面 PAD,AD⊂平面 PAD,所以 BC∥平面 PAD.又平面 PAD∩平面 PBC=l,BC⊂平面 PBC,所以 l∥BC. (2)解 MN∥平面 PAD. 证明如下:如图,取 PD 的中点 E,连接 AE,NE, 则 NE∥CD,NE=1 2 CD
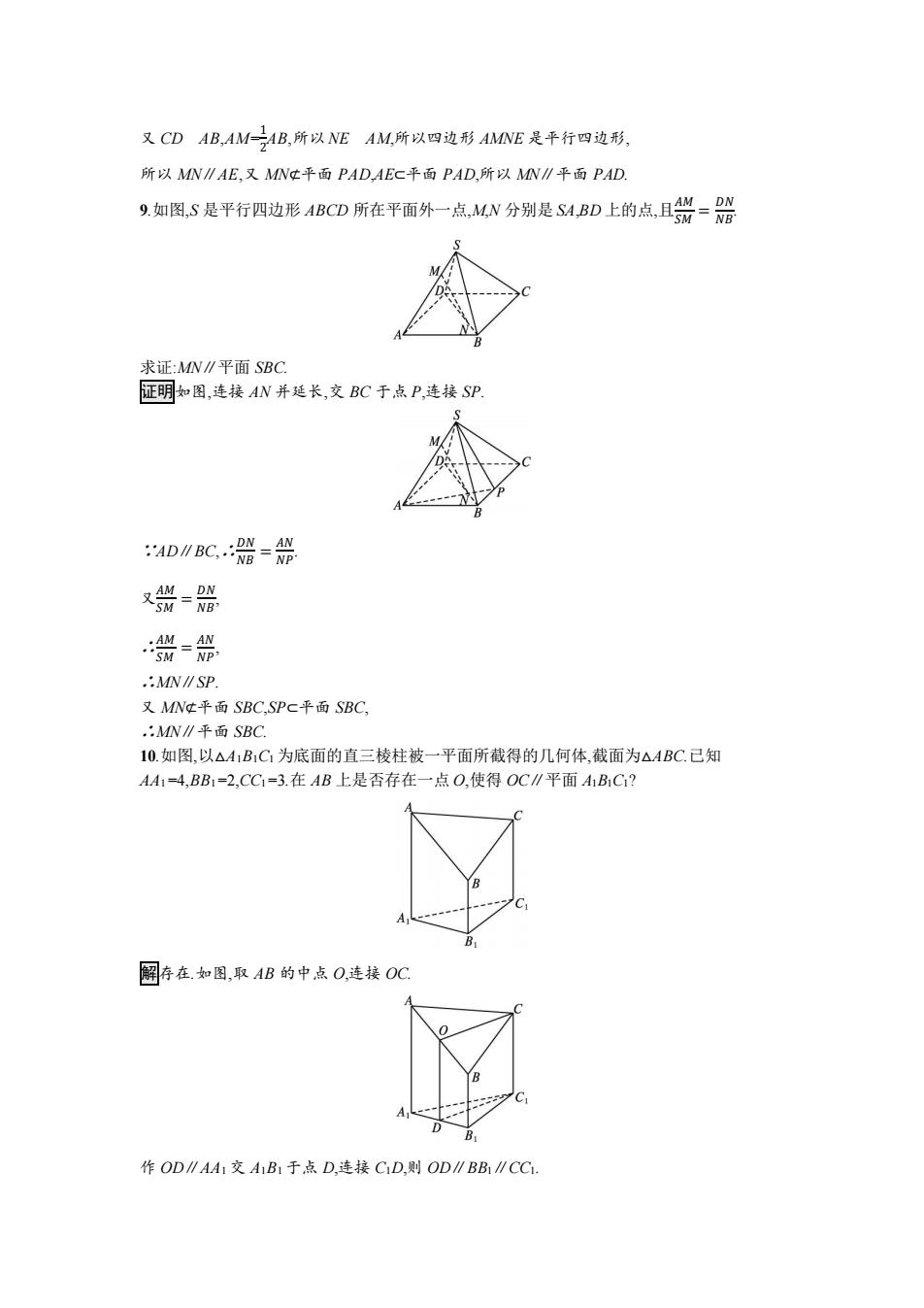
又CDAB,AM-AB,所以NEAM,所以四边形AMNE是平行四边形, 所以MN∥AE,又MNt平面PAD,AEC平面PAD,所以MN∥平面PAD. 9如图,S是平行四边形ABCD所在平面外一点MN分别是S1BD上的点,且兴-器 求证:MN∥平面SBC 证明如图,连接AN并延长,交BC于点P,连接SP :AD∥BC器= NP 又兴-器 兴 .:MW∥SP 又MNt平面SBC,SPc平面SBC, .:MN∥平面SBC. 10.如图,以△41B1C为底面的直三棱柱被一平面所截得的几何体,截面为△ABC.己知 A4A1=4,BB1=2,CC1=3.在AB上是否存在一点O,使得OC∥平面A1B1C1? 阔存在.如图,取AB的中点O,连接0C A B 作OD∥AA1交AB1于点D,连接CD,则OD∥BB1∥CC
又 CD AB,AM=1 2 AB,所以 NE AM,所以四边形 AMNE 是平行四边形, 所以 MN∥AE,又 MN⊄平面 PAD,AE⊂平面 PAD,所以 MN∥平面 PAD. 9.如图,S 是平行四边形 ABCD 所在平面外一点,M,N 分别是 SA,BD 上的点,且 𝐴𝑀 𝑆𝑀 = 𝐷𝑁 𝑁𝐵. 求证:MN∥平面 SBC. 证明如图,连接 AN 并延长,交 BC 于点 P,连接 SP. ∵AD∥BC,∴ 𝐷𝑁 𝑁𝐵 = 𝐴𝑁 𝑁𝑃. 又 𝐴𝑀 𝑆𝑀 = 𝐷𝑁 𝑁𝐵, ∴ 𝐴𝑀 𝑆𝑀 = 𝐴𝑁 𝑁𝑃, ∴MN∥SP. 又 MN⊄平面 SBC,SP⊂平面 SBC, ∴MN∥平面 SBC. 10.如图,以△A1B1C1 为底面的直三棱柱被一平面所截得的几何体,截面为△ABC.已知 AA1=4,BB1=2,CC1=3.在 AB 上是否存在一点 O,使得 OC∥平面 A1B1C1? 解存在.如图,取 AB 的中点 O,连接 OC. 作 OD∥AA1 交 A1B1 于点 D,连接 C1D,则 OD∥BB1∥CC1

因为0是AB的中点,所以OD-4A1+BB1)=3=CC,则四边形ODCC是平行四边形,所以 OC∥CD. 又C1DC平面A1B1C1,且OCt平面A1B1C,所以OC∥平面A1B1C,即在边AB上存在一点O, 使得OC∥平面AB1C1
因为 O 是 AB 的中点,所以 OD=1 2 (AA1+BB1)=3=CC1,则四边形 ODC1C 是平行四边形,所以 OC∥C1D. 又 C1D⊂平面 A1B1C1,且 OC⊄平面 A1B1C1,所以 OC∥平面 A1B1C1,即在边 AB 上存在一点 O, 使得 OC∥平面 A1B1C1