
第2课时直线与平面垂直的性质定理 课后·训练提升 1.在正方体ABCD-A1B1C1D1中,若直线I(与直线BB1不重合)⊥平面A1B1CD1,则( A.B1B⊥I B.B1B∥I C.B1B与I异面但不垂直 D.B1B与I相交但不垂直 答案B 2.己知m,n为异面直线,m⊥平面a,n⊥平面B,直线1满足1Lm,1Ln,l仗a,1¢B,则()】 A.a∥B且l∥a B.a⊥B且1⊥B C.a与B相交,且交线垂直于1 D.a与B相交,且交线平行于1 答案D 解析若a∥B,则由m上a知m⊥B,而n⊥B,所以m∥n,与mn为异面直线矛盾,所以平面a与 平面B相交 由m⊥平面a,m⊥1,且1¢a,可知I∥a,同理,l∥B,所以1与两平面的交线平行.故选D. 3.已知直线I与平面a相交于点O,A∈I,B∈I,AEa,BEa且OA=AB.若AC⊥平面a,垂足为 C,BD⊥平面a,垂足为D,AC=1,则BD=(). A.2 B.1 c D 答案A 解析如图,因为AC⊥平面a,BD⊥平面a所以AC∥BD 连接OD,所以器=品 因为OA=AB, 所以器-号 因为AC=L,所以BD=2 4.已知地面上有两根相距am的竖直的旗杆,它们的高度分别是bm和cm(b>c),则它们顶端 之间的距离为 m. 窨案a2+(b-c)2 解析如图,根据题意可知AD=bm,BC=cm,AB=am. 由线面垂直的性质定理可得AD∥BC
第 2 课时 直线与平面垂直的性质定理 课后· 1.在正方体 ABCD-A1B1C1D1 中,若直线 l(与直线 BB1 不重合)⊥平面 A1B1C1D1,则( ). A.B1B⊥l B.B1B∥l C.B1B 与 l 异面但不垂直 D.B1B 与 l 相交但不垂直 答案 B 2.已知 m,n 为异面直线,m⊥平面 α,n⊥平面 β,直线 l 满足 l⊥m,l⊥n,l⊄α,l⊄β,则( ). A.α∥β 且 l∥α B.α⊥β 且 l⊥β C.α 与 β 相交,且交线垂直于 l D.α 与 β 相交,且交线平行于 l 答案 D 解析若 α∥β,则由 m⊥α 知 m⊥β,而 n⊥β,所以 m∥n,与 m,n 为异面直线矛盾,所以平面 α 与 平面 β 相交. 由 m⊥平面 α,m⊥l,且 l⊄α,可知 l∥α,同理,l∥β,所以 l 与两平面的交线平行.故选 D. 3.已知直线 l 与平面 α 相交于点 O,A∈l,B∈l,A∉α,B∉α,且 OA=AB.若 AC⊥平面 α,垂足为 C,BD⊥平面 α,垂足为 D,AC=1,则 BD=( ). A.2 B.1 C. 3 2 D. 1 2 答案 A 解析如图,因为 AC⊥平面 α,BD⊥平面 α,所以 AC∥BD. 连接 OD,所以𝑂𝐴 𝑂𝐵 = 𝐴𝐶 𝐵𝐷. 因为 OA=AB, 所以𝑂𝐴 𝑂𝐵 = 1 2 . 因为 AC=1,所以 BD=2. 4.已知地面上有两根相距 a m 的竖直的旗杆,它们的高度分别是 b m 和 c m(b>c),则它们顶端 之间的距离为 m. 答案√𝑎 2 + (𝑏-𝑐) 2 解析如图,根据题意可知 AD=b m,BC=c m,AB=a m. 由线面垂直的性质定理可得 AD∥BC
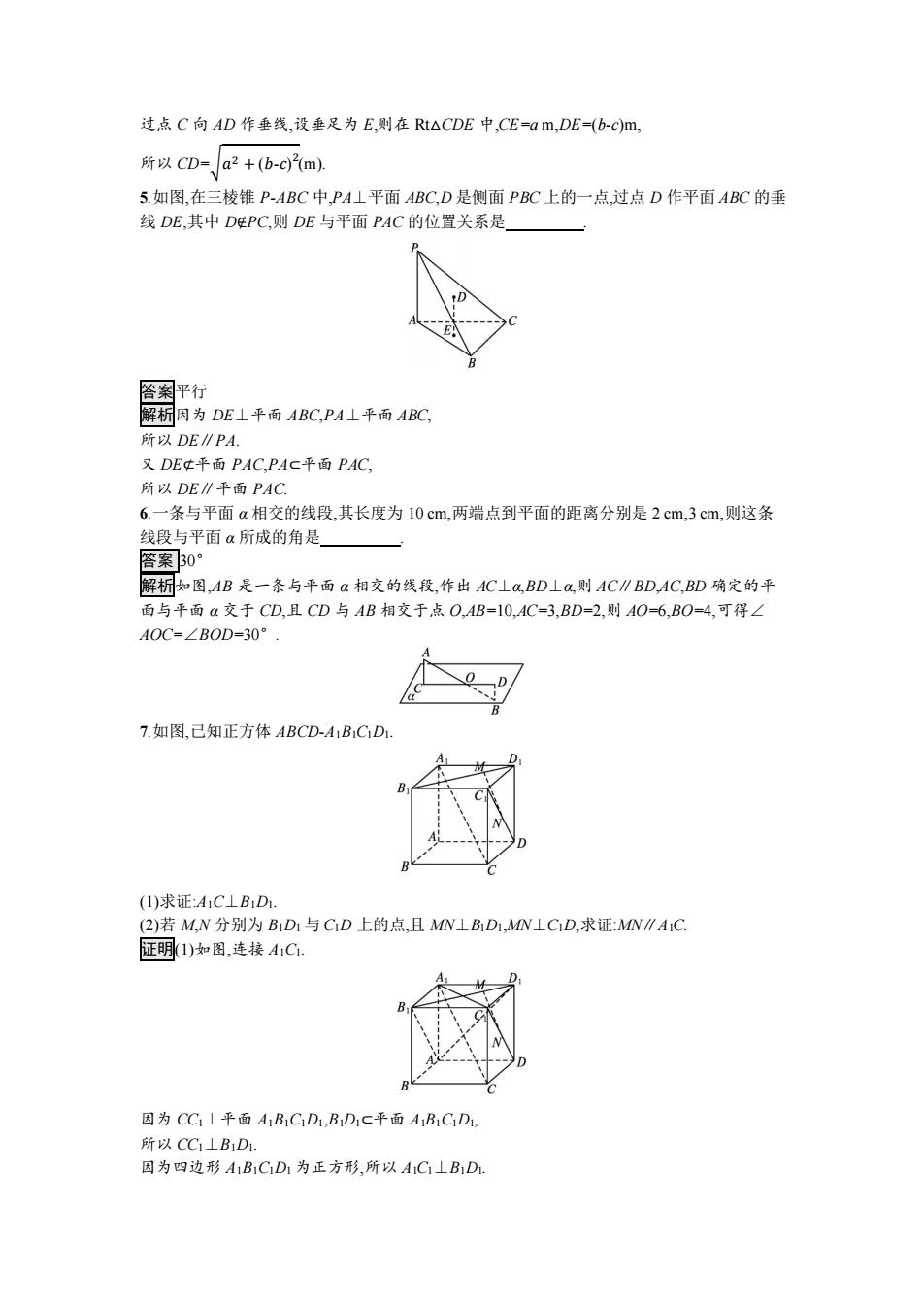
过,点C向AD作垂线,设垂足为E,则在Rt△CDE中,CE=am,DE=(b-c)m, 所以CD=a2+(b-cm 5.如图,在三棱锥P-ABC中,PA⊥平面ABC,D是侧面PBC上的一点,过点D作平面ABC的垂 线DE,其中DEPC,则DE与平面PAC的位置关系是 答案平行 解桐因为DE⊥平面ABC,PA⊥平面ABC, 所以DE∥PA. 又DEt平面PAC,PAC平面PAC, 所以DE∥平面PAC 6.一条与平面a相交的线段,其长度为10cm,两端点到平面的距离分别是2cm,3cm,则这条 线段与平面α所成的角是 答案}30° 解析如图,AB是一条与平面a相交的线段,作出AC⊥a,BD⊥a,则AC∥BD,AC,BD确定的平 面与平面a交于CD,且CD与AB相交于点O,AB=10,AC=3,BD=2,则AO=6,BO=4,可得∠ AOC=∠BOD=30°· D 7.如图,己知正方体ABCD-A1B1CD1. (1)求证:A1C⊥B1D1. (2)若M,N分别为B1D1与CD上的点,且MN⊥BD1,MN⊥CD,求证:MN∥AC 证明1)如图,连接41C. 因为CC1⊥平面A1B1C1D1,BD1C平面AB1CD1, 所以CC1⊥B1D1. 因为四边形A1B1CD1为正方形,所以AC1⊥B1D1
过点 C 向 AD 作垂线,设垂足为 E,则在 Rt△CDE 中,CE=a m,DE=(b-c)m, 所以 CD=√𝑎 2 + (𝑏-𝑐) 2 (m). 5.如图,在三棱锥 P-ABC 中,PA⊥平面 ABC,D 是侧面 PBC 上的一点,过点 D 作平面 ABC 的垂 线 DE,其中 D∉PC,则 DE 与平面 PAC 的位置关系是 . 答案平行 解析因为 DE⊥平面 ABC,PA⊥平面 ABC, 所以 DE∥PA. 又 DE⊄平面 PAC,PA⊂平面 PAC, 所以 DE∥平面 PAC. 6.一条与平面 α 相交的线段,其长度为 10 cm,两端点到平面的距离分别是 2 cm,3 cm,则这条 线段与平面 α 所成的角是 . 答案 30° 解析如图,AB 是一条与平面 α 相交的线段,作出 AC⊥α,BD⊥α,则 AC∥BD,AC,BD 确定的平 面与平面 α 交于 CD,且 CD 与 AB 相交于点 O,AB=10,AC=3,BD=2,则 AO=6,BO=4,可得∠ AOC=∠BOD=30°. 7.如图,已知正方体 ABCD-A1B1C1D1. (1)求证:A1C⊥B1D1. (2)若 M,N 分别为 B1D1 与 C1D 上的点,且 MN⊥B1D1,MN⊥C1D,求证:MN∥A1C. 证明(1)如图,连接 A1C1. 因为 CC1⊥平面 A1B1C1D1,B1D1⊂平面 A1B1C1D1, 所以 CC1⊥B1D1. 因为四边形 A1B1C1D1 为正方形,所以 A1C1⊥B1D1

又CC∩41C=C1,所以B1D1⊥平面ACC 又A1CC平面A1CC,所以A1C⊥B1D1. (2)如图,连接AB1,AD1. 因为B1CAD,所以四边形ADCB1为平行四边形,所以CD∥AB1. 因为MN⊥CD,所以MN LAB1. 又MN⊥B1D1,AB1∩B1D1=B1 所以MN⊥平面AB1D1, 由(I)知A1C⊥B1D1,同理可得A1C⊥AB1. 因为AB1∩B1D1=B1,所以A1C⊥平面AB1D1: 所以MN∥A1C. 8.如图,△ABC是等边三角形,AE和CD都垂直于平面ABC,且AE=AB=-2a,CD=a,F是BE的中 点,求证 (I)DF∥平面ABC (2)AF⊥BD. 证明1)如图,取AB的中点G,连接FG,CG 因为F为BE的中点, 所以FG∥AE,FG-AE. 因为CD⊥平面ABC,AE⊥平面ABC,所以CD∥AE. 因为CD-AE,所以FG∥CD,FG=CD, 所以四边形CDFG是平行四边形,所以DF∥CG. 因为CGC平面ABC,DFt平面ABC, 所以DF∥平面ABC (2)在Rt△ABE中,AE=2a,AB=2a,F为BE的中点,所以AF⊥BE 因为△ABC是等边三角形, 所以CG⊥AB.所以DF⊥AB 因为FG⊥平面ABC,所以FG⊥GC,FG⊥DF 因为FG∩AB=G,所以DF⊥平面ABE. 因为AFC平面ABE,所以DF⊥AF 因为BE∩DF=F,所以AF⊥平面BDF 因为BDC平面BDF,所以AF⊥BD. 9.如图,在三棱柱ABC-A1B1C中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1CC
又 CC1∩A1C1=C1,所以 B1D1⊥平面 A1C1C. 又 A1C⊂平面 A1C1C,所以 A1C⊥B1D1. (2)如图,连接 AB1,AD1. 因为 B1C1 AD,所以四边形 ADC1B1 为平行四边形,所以 C1D∥AB1. 因为 MN⊥C1D,所以 MN⊥AB1. 又 MN⊥B1D1,AB1∩B1D1=B1, 所以 MN⊥平面 AB1D1. 由(1)知 A1C⊥B1D1,同理可得 A1C⊥AB1. 因为 AB1∩B1D1=B1,所以 A1C⊥平面 AB1D1. 所以 MN∥A1C. 8.如图,△ABC 是等边三角形,AE 和 CD 都垂直于平面 ABC,且 AE=AB=2a,CD=a,F 是 BE 的中 点,求证: (1)DF∥平面 ABC; (2)AF⊥BD. 证明(1)如图,取 AB 的中点 G,连接 FG,CG. 因为 F 为 BE 的中点, 所以 FG∥AE,FG=1 2 AE. 因为 CD⊥平面 ABC,AE⊥平面 ABC,所以 CD∥AE. 因为 CD=1 2 AE,所以 FG∥CD,FG=CD. 所以四边形 CDFG 是平行四边形,所以 DF∥CG. 因为 CG⊂平面 ABC,DF⊄平面 ABC, 所以 DF∥平面 ABC. (2)在 Rt△ABE 中,AE=2a,AB=2a,F 为 BE 的中点,所以 AF⊥BE. 因为△ABC 是等边三角形, 所以 CG⊥AB,所以 DF⊥AB. 因为 FG⊥平面 ABC,所以 FG⊥GC,FG⊥DF. 因为 FG∩AB=G,所以 DF⊥平面 ABE. 因为 AF⊂平面 ABE,所以 DF⊥AF. 因为 BE∩DF=F,所以 AF⊥平面 BDF. 因为 BD⊂平面 BDF,所以 AF⊥BD. 9.如图,在三棱柱 ABC-A1B1C1 中,侧面 BB1C1C 为菱形,B1C 的中点为 O,且 AO⊥平面 BB1C1C

(1)求证:B1C⊥AB; (2)若AC⊥AB1,∠CBB1=60°,BC=1,求三棱柱ABC-4B1C1两底面间的距离 (1证明如图,连接BC1,则O为BC与B1C的交点 因为侧面BB1CC为菱形,所以B1C⊥BC1,又AO⊥平面BBC1C, 所以B1C⊥AO. 又AOnBC=O, 所以B1C⊥平面ABO, 又ABC平面ABO,所以BC⊥AB (2解国为四边形BB1CC为菱形,BC=1,∠CBB1=60°,所以△BCB1为正三角形,所以 BC=1.0BSc, 因为AO⊥平面BB1CC, 所以AO⊥BC1,AO⊥B1C. 又0为B,C的中点,ACLAB,所以△1B,C为等腰直角三角形,所以A0三4C-号 所以AB=VA02+0B2=1. 在△MBC中,cos∠ABC82AC-寻所以sn∠ABC- 2AB·BC SAABC-TAB-BCsin∠ABC= 8 设三棱柱ABC-A1B1C1两底面间的距离为h,则,点B1到平面ABC的距离为h 因为MBCB,=aABc,即时Sw,40-字a4ch,所以h牙 故三棱柱ABCA1B1C两底面间的距离为 7
(1)求证:B1C⊥AB; (2)若 AC⊥AB1,∠CBB1=60°,BC=1,求三棱柱 ABC-A1B1C1 两底面间的距离. (1)证明如图,连接 BC1,则 O 为 BC1 与 B1C 的交点. 因为侧面 BB1C1C 为菱形,所以 B1C⊥BC1,又 AO⊥平面 BB1C1C, 所以 B1C⊥AO. 又 AO∩BC1=O, 所以 B1C⊥平面 ABO, 又 AB⊂平面 ABO,所以 B1C⊥AB. (2)解因为四边形 BB1C1C 为菱形,BC=1,∠CBB1=60°,所以△BCB1 为正三角形,所以 B1C=1,OB=√3 2 , 𝑆△𝐵𝐶𝐵1 = √3 4 . 因为 AO⊥平面 BB1C1C, 所以 AO⊥BC1,AO⊥B1C. 又 O 为 B1C 的中点,AC⊥AB1,所以△AB1C 为等腰直角三角形,所以 AO=1 2 ,AC=√2 2 . 所以 AB=√𝐴𝑂2 + 𝑂𝐵2=1. 在△ABC 中,cos∠ABC=𝐴𝐵 2+𝐵𝐶 2 -𝐴𝐶 2 2𝐴𝐵·𝐵𝐶 = 3 4 ,所以 sin∠ABC=√7 4 ,S△ABC= 1 2 AB·BC·sin∠ABC=√7 8 . 设三棱柱 ABC-A1B1C1 两底面间的距离为 h,则点 B1 到平面 ABC 的距离为 h. 因为𝑉𝐴-𝐵𝐶𝐵1 = 𝑉𝐵1-𝐴𝐵𝐶,即 1 3 𝑆△𝐵𝐶𝐵1·AO=1 3 S△ABC·h,所以 h=√21 7 . 故三棱柱 ABC-A1B1C1 两底面间的距离为√21 7