
8.2立体图形的直观图 课后·训练提升 1.(多选题)有关用斜二测画法画水平放置的图形的直观图,下列描述正确的是(). A.三角形的直观图仍然是一个三角形 B.90°的角的直观图会变为45°的角 C.与y轴平行的线段长度变为原来的一半 D.由于选轴的不同,所得的直观图可能不同 含案ACD 解桐对于A,根据斜二测画法特点知,相交直线的直观图仍是相交直线,因此三角形的直观图 仍是一个三角形,故A正确:对于B,90°的角的直观图会变为45°或135°的角,故B错 误;C,D显然正确. 2.水平放置的△ABC,有一边在水平线上,用斜二测画法得到它的直观图是正三角形A'B'C,则 △ABC是()】 A.锐角三角形 B直角三角形 C钝角三角形 D.任意三角形 客案c 解析如图,将直观图还原为平面图形,可知△ABC是钝角三角形 y 3.如图,矩形O'A'B'C是水平放置的一个平面图形的直观图,其中OA'=6,O'C”=2,则原图形是 (). A正方形 B.矩形 C.菱形 D.梯形 答案c 4一个建筑物上部为四棱锥.下部为长方体,且四棱锥的底面与长方体的上底面尺寸相同,已知 长方体的长、宽、高分别为20m,5m,10m,四棱锥的高为8m,若按1:500的比例画出它的 直观图,那么直观图中,长方体的长、宽、高和棱锥的高应分别为(). A.4 cm,1 cm,2 cm,1.6 cm B.4 cm,0.5 cm,2 cm,0.8 cm C.4 cm,0.5 cm,2 cm,1.6 cm D.2 cm,0.5 cm,1 cm,0.8 cm 答案 解析由比例尺可知缩小后的长方体的长、宽、高和四棱锥的高分别为4cm,1cm,2cm和1.6 cm,再结合斜二测画法,可知直观图的相应尺寸应分别为4cm,0.5cm,2cm,1.6cm 5.如图,△A'O'B表示水平放置的△AOB的直观图,B在x轴上,A'O和x轴垂直,且A'O'=2,则 △AOB的边OB上的高为()
8.2 立体图形的直观图 课后· 1.(多选题)有关用斜二测画法画水平放置的图形的直观图,下列描述正确的是( ). A.三角形的直观图仍然是一个三角形 B.90°的角的直观图会变为 45°的角 C.与 y 轴平行的线段长度变为原来的一半 D.由于选轴的不同,所得的直观图可能不同 答案 ACD 解析对于 A,根据斜二测画法特点知,相交直线的直观图仍是相交直线,因此三角形的直观图 仍是一个三角形,故 A 正确;对于 B,90°的角的直观图会变为 45°或 135°的角,故 B 错 误;C,D 显然正确. 2.水平放置的△ABC,有一边在水平线上,用斜二测画法得到它的直观图是正三角形 A'B'C',则 △ABC 是( ). A.锐角三角形 B.直角三角形 C.钝角三角形 D.任意三角形 答案 C 解析如图,将直观图还原为平面图形,可知△ABC 是钝角三角形. 3.如图,矩形 O'A'B'C'是水平放置的一个平面图形的直观图,其中 O'A'=6,O'C'=2,则原图形是 ( ). A.正方形 B.矩形 C.菱形 D.梯形 答案 C 4.一个建筑物上部为四棱锥,下部为长方体,且四棱锥的底面与长方体的上底面尺寸相同,已知 长方体的长、宽、高分别为 20 m,5 m,10 m,四棱锥的高为 8 m,若按 1∶500 的比例画出它的 直观图,那么直观图中,长方体的长、宽、高和棱锥的高应分别为( ). A.4 cm,1 cm,2 cm,1.6 cm B.4 cm,0.5 cm,2 cm,0.8 cm C.4 cm,0.5 cm,2 cm,1.6 cm D.2 cm,0.5 cm,1 cm,0.8 cm 答案 C 解析由比例尺可知缩小后的长方体的长、宽、高和四棱锥的高分别为 4 cm,1 cm,2 cm 和 1.6 cm,再结合斜二测画法,可知直观图的相应尺寸应分别为 4 cm,0.5 cm,2 cm,1.6 cm. 5.如图,△A'O'B'表示水平放置的△AOB 的直观图,B'在 x'轴上,A'O'和 x'轴垂直,且 A'O'=2,则 △AOB 的边 OB 上的高为( )

15 A.2 B.4 C.2v2 D.4v2 答案D 解杨设△40B的边OB上的高为么,由题意得S原=2V2S属,所以0B-h=2VZ×2×0B: 因为OB=OB',所以h=4VZ.故选D. 6.已知两个圆锥,底面重合在一起,其中一个圆锥顶点到底面的距离为2cm,另一个圆锥项点 到底面的距离为3cm,则其直观图中这两个顶点之间的距离为(). A.2cm B.3cm C.2.5cm D.5 cm 答案D 解析由题意知其直观图如图所示,由图可知两个顶点之间的距离为5cm.故选D, 7.己知用斜二测画法,画得的正方形的直观图面积为18√2,则原正方形的面积 为 答案72 解析如图,作出正方形OABC的直观图OA'B'C,作CDLx'轴于点D D S直观国=O'A'×CD: 又S玉方弱=OC×OA, 所以正透 OCXOA 5直观图 OA'XCD 又在Rt△OD'C'中,O'C=V2CD' 即CD0C结合平面图与直观图的关系可知0A=0A0C-20C 所以题=0CA=29C=2V2 3直观图0Ax0c0c 又S现喝=18√Z, 所以S*制=2VZ×18VZ-72. 8.如图,正方形A'B'CD的边长为1,己知该正方形是某个水平放置的四边形用斜二测画法画 出的直观图,试画出原图形并求出其面积
A.2 B.4 C.2√2 D.4√2 答案 D 解析设△AOB 的边 OB 上的高为 h,由题意得 S 原图形=2√2S 直观图,所以1 2 OB·h=2√2 × 1 2 ×2×O'B'. 因为 OB=O'B',所以 h=4√2.故选 D. 6.已知两个圆锥,底面重合在一起,其中一个圆锥顶点到底面的距离为 2 cm,另一个圆锥顶点 到底面的距离为 3 cm,则其直观图中这两个顶点之间的距离为( ). A.2 cm B.3 cm C.2.5 cm D.5 cm 答案 D 解析由题意知其直观图如图所示,由图可知两个顶点之间的距离为 5 cm.故选 D. 7.已知用斜二测画法,画得的正方形的直观图面积为 18√2,则原正方形的面积 为 . 答案 72 解析如图,作出正方形 OABC 的直观图 O'A'B'C',作 C'D'⊥x'轴于点 D'. S 直观图=O'A'×C'D'. 又 S 正方形=OC×OA, 所以 𝑆正方形 𝑆直观图 = 𝑂𝐶×𝑂𝐴 𝑂'𝐴'×𝐶'𝐷' , 又在 Rt△O'D'C'中,O'C'=√2C'D', 即 C'D'=√2 2 O'C',结合平面图与直观图的关系可知 OA=O'A',OC=2O'C', 所以 𝑆正方形 𝑆直观图 = 𝑂𝐶×𝑂𝐴 𝑂𝐴× √2 2 𝑂'𝐶' = 2𝑂'𝐶' √2 2 𝑂'𝐶' =2√2. 又 S 直观图=18√2, 所以 S 正方形=2√2×18√2=72. 8.如图,正方形 A'B'C'D'的边长为 1,已知该正方形是某个水平放置的四边形用斜二测画法画 出的直观图,试画出原图形并求出其面积
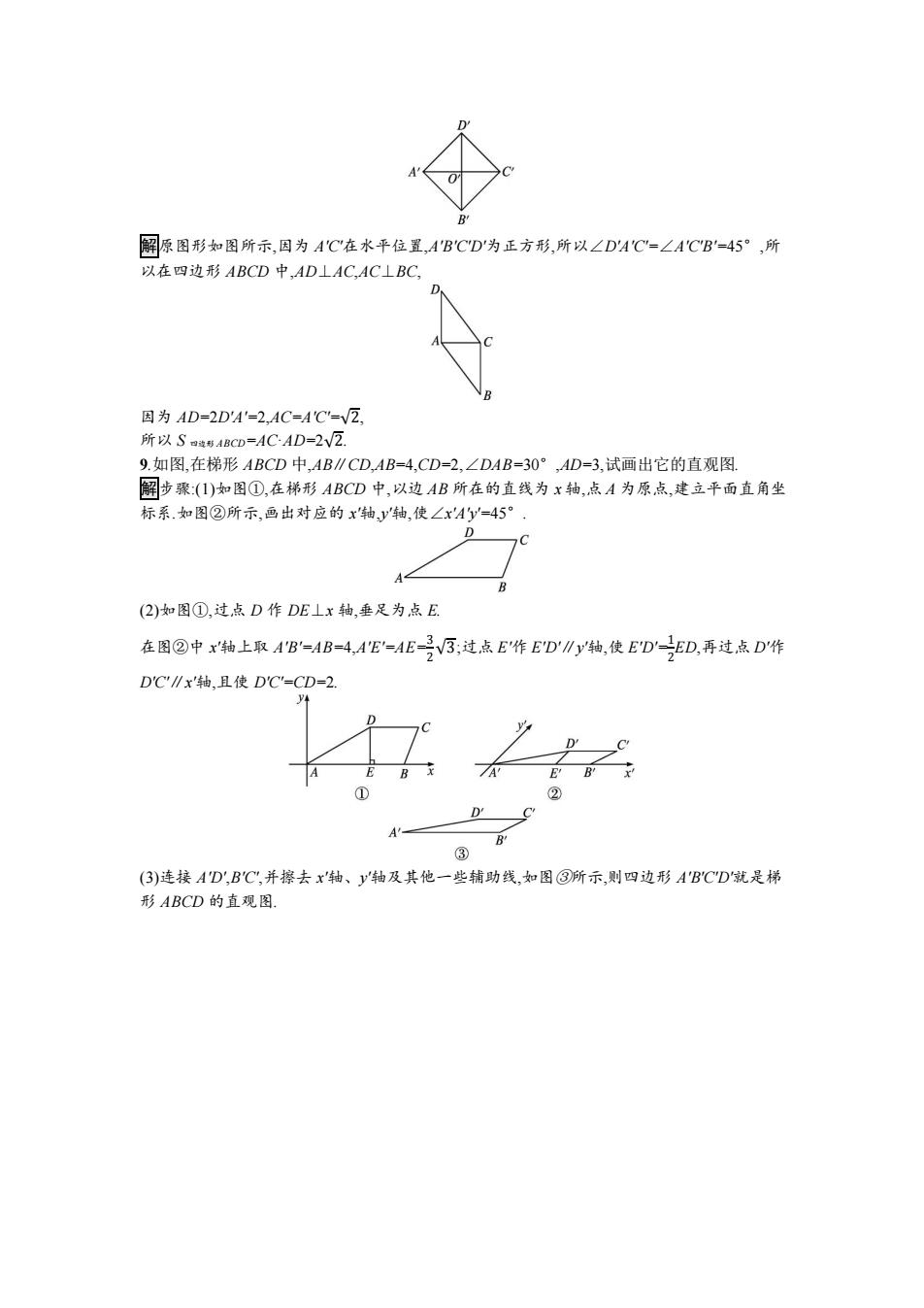
解原图形如图所示,因为AC在水平位置,ABCD为正方形,所以∠DAC=∠ACB'-45°,所 以在四边形ABCD中,AD⊥AC,AC⊥BC, 因为AD=2DA'-2,AC=A'C=V2 所以Sg形ABCD=ACAD=2V2. 9.如图,在梯形ABCD中,AB∥CD,AB=4,CD=2,∠DAB=30°,AD=3,试画出它的直观图. 解步骤(I)如图①,在梯形ABCD中,以边AB所在的直线为x轴,点A为原点,建立平面直角坐 标系.如图②所示,画出对应的x轴,y轴,使∠xAy=45°, D A (2)如图①,过,点D作DE⊥x轴,垂足为点E 在图②中x轴上取A'B'=AB=4,AE=AE-V3:过点E作E'D'∥y轴,使EDED,再过点D作 DC'∥x轴,且使D'C=CD=2 E B ② A' ③ (3)连接A'D',BC',并擦去x轴、y轴及其他一些辅助线,如图③所示,则四边形AB'CD就是梯 形ABCD的直观图
解原图形如图所示,因为 A'C'在水平位置,A'B'C'D'为正方形,所以∠D'A'C'=∠A'C'B'=45°,所 以在四边形 ABCD 中,AD⊥AC,AC⊥BC, 因为 AD=2D'A'=2,AC=A'C'=√2, 所以 S 四边形 ABCD=AC·AD=2√2. 9.如图,在梯形 ABCD 中,AB∥CD,AB=4,CD=2,∠DAB=30°,AD=3,试画出它的直观图. 解步骤:(1)如图①,在梯形 ABCD 中,以边 AB 所在的直线为 x 轴,点 A 为原点,建立平面直角坐 标系.如图②所示,画出对应的 x'轴,y'轴,使∠x'A'y'=45°. (2)如图①,过点 D 作 DE⊥x 轴,垂足为点 E. 在图②中 x'轴上取 A'B'=AB=4,A'E'=AE=3 2 √3;过点 E'作 E'D'∥y'轴,使 E'D'=1 2 ED,再过点 D'作 D'C'∥x'轴,且使 D'C'=CD=2. (3)连接 A'D',B'C',并擦去 x'轴、y'轴及其他一些辅助线,如图③所示,则四边形 A'B'C'D'就是梯 形 ABCD 的直观图