第1课时棱柱、棱锥、棱台的结构特征 课后·训练提升 1.(多选题)下列说法错误的是() A.有2个面平行,其余各面都是梯形的几何体是棱台 B.多面体至少有3个面 C.各侧面都是正方形的四棱柱一定是正方体 D.九棱柱有9条侧棱,9个侧面,侧面为平行四边形 答案ABC 解桐选项A错误,反例如图①所示;一个多面体至少有4个面,如三棱锥有4个面,不存在只有 3个面的多面体,所以选项B错误:选项C错误,反例如图②所示,上、下底面是全等的菱形,各 侧面是全等的正方形,它不是正方体:根据棱柱的定义,知选项D正确 ② 2.在下列四个平面图形中,每个小四边形皆为正方形,其中可以沿相邻正方形的公共边折叠围 成一个正方体的图形是( 答案 3在棱柱中,不同在任何侧面,且不同在任何底面的两个顶点的连线称为它的对角线,则一个五 棱柱的对角线的条数为() A.20 B.15 C.12 D.10 答案D 解桐如图,在五棱柱ABCDE-A1B1CD1E1中,从顶点A出发的对角线有两条,同理从点B,C,D,E 出发的对角线均有两条,共2×5=10(条). D 4.如图,在正方体ABCD-A1B1CD1中,下列关于多面体ACB1D1的说法正确的个数是()
第 1 课时 棱柱、棱锥、棱台的结构特征 课后· 1.(多选题)下列说法错误的是( ). A.有 2 个面平行,其余各面都是梯形的几何体是棱台 B.多面体至少有 3 个面 C.各侧面都是正方形的四棱柱一定是正方体 D.九棱柱有 9 条侧棱,9 个侧面,侧面为平行四边形 答案 ABC 解析选项 A 错误,反例如图①所示;一个多面体至少有 4 个面,如三棱锥有 4 个面,不存在只有 3 个面的多面体,所以选项 B 错误;选项 C 错误,反例如图②所示,上、下底面是全等的菱形,各 侧面是全等的正方形,它不是正方体;根据棱柱的定义,知选项 D 正确. ① ② 2.在下列四个平面图形中,每个小四边形皆为正方形,其中可以沿相邻正方形的公共边折叠围 成一个正方体的图形是( ). 答案 C 3.在棱柱中,不同在任何侧面,且不同在任何底面的两个顶点的连线称为它的对角线,则一个五 棱柱的对角线的条数为( ). A.20 B.15 C.12 D.10 答案 D 解析如图,在五棱柱 ABCDE-A1B1C1D1E1 中,从顶点 A 出发的对角线有两条,同理从点 B,C,D,E 出发的对角线均有两条,共 2×5=10(条). 4.如图,在正方体 ABCD-A1B1C1D1 中,下列关于多面体 ACB1D1 的说法正确的个数是( )
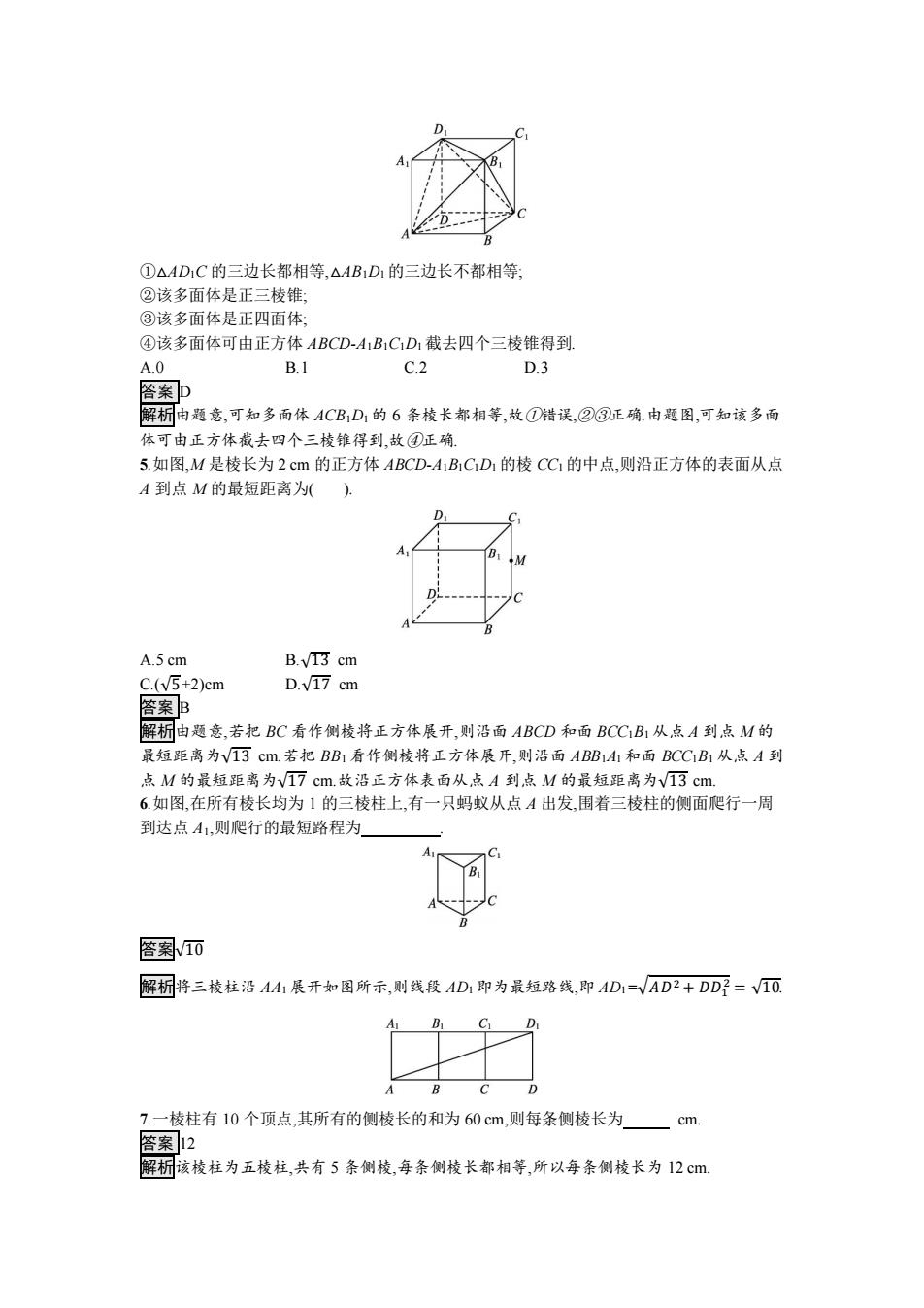
①△AD1C的三边长都相等,△AB1D1的三边长不都相等; ②该多面体是正三棱锥: ③该多面体是正四面体: ④该多面体可由正方体ABCD-A1B1C1D1截去四个三棱锥得到. A.0 B.1 C.2 D.3 答案p 解析由题意,可知多面体ACBD1的6条棱长都相等,故①错误,②③正确.由题图,可知该多面 体可由正方体截去四个三棱锥得到,故④正确 5.如图,M是棱长为2cm的正方体ABCD-A1B1CD1的棱CC的中点,则沿正方体的表面从点 A到点M的最短距离为(). D D A.5 cm B.v13 cm C.(V5+2)cm D.√17cm 答案B 解析由题意,若把BC看作侧棱将正方体展开,则沿面ABCD和面BCCB1从点A到,点M的 最短距离为VI3cm.若把BB1看作侧棱将正方体展开,则沿面ABB1A1和面BCCB1从点A到 点M的最短距离为VI7cm.故沿正方体表面从点A到,点M的最短距离为√3cm 6.如图,在所有棱长均为1的三棱柱上,有一只蚂蚁从点A出发,围着三棱柱的侧面爬行一周 到达点A1,则爬行的最短路程为 含案V而 解析將三棱柱沿A41展开如图所示,则线段AD1即为最短路线,即AD1=√AD2+DD?=V而 B1 C1 D A B C D 7.一棱柱有10个顶点,其所有的侧棱长的和为60cm,则每条侧棱长为一 cm 答案2 解析该棱柱为五棱柱,共有5条侧棱,每条侧棱长都相等,所以每条侧棱长为12cm
①△AD1C 的三边长都相等,△AB1D1 的三边长不都相等; ②该多面体是正三棱锥; ③该多面体是正四面体; ④该多面体可由正方体 ABCD-A1B1C1D1 截去四个三棱锥得到. A.0 B.1 C.2 D.3 答案 D 解析由题意,可知多面体 ACB1D1 的 6 条棱长都相等,故①错误,②③正确.由题图,可知该多面 体可由正方体截去四个三棱锥得到,故④正确. 5.如图,M 是棱长为 2 cm 的正方体 ABCD-A1B1C1D1 的棱 CC1 的中点,则沿正方体的表面从点 A 到点 M 的最短距离为( ). A.5 cm B.√13 cm C.(√5+2)cm D.√17 cm 答案 B 解析由题意,若把 BC 看作侧棱将正方体展开,则沿面 ABCD 和面 BCC1B1 从点 A 到点 M 的 最短距离为√13 cm.若把 BB1 看作侧棱将正方体展开,则沿面 ABB1A1 和面 BCC1B1 从点 A 到 点 M 的最短距离为√17 cm.故沿正方体表面从点 A 到点 M 的最短距离为√13 cm. 6.如图,在所有棱长均为 1 的三棱柱上,有一只蚂蚁从点 A 出发,围着三棱柱的侧面爬行一周 到达点 A1,则爬行的最短路程为 . 答案√10 解析将三棱柱沿 AA1 展开如图所示,则线段 AD1 即为最短路线,即 AD1=√𝐴𝐷2 + 𝐷𝐷1 2 = √10. 7.一棱柱有 10 个顶点,其所有的侧棱长的和为 60 cm,则每条侧棱长为 cm. 答案 12 解析该棱柱为五棱柱,共有 5 条侧棱,每条侧棱长都相等,所以每条侧棱长为 12 cm

8.下列说法正确的是 (填序号) ①棱柱的所有面都是四边形 ②一个棱柱至少有五个面: ③棱锥被平面分成的两部分不可能都是棱锥: ④棱柱被平面分成的两部分可以都是棱柱: ⑤棱台的上底面的面积与下底面的面积之比一定小于1 答案2④⑤ 解析和错误,棱柱的所有侧面都是平行四边形,而底面不一定是四边形:②正确;③错误,如图, 四棱锥被截面PBD分成的两部分都是棱锥:④正确:⑤正确,由棱台的定义知,棱台是由棱锥截 得的,截面是棱台的上底面,故上底面的面积一定小于下底面的面积 9.如图,在边长为2a的正方形ABCD中,E,F分别为AB,BC的中点,沿图中虚线将3个三角形 折起,使点A,B,C重合,重合后记为点P.问: (1)折起后形成的几何体是什么几何体? (2)这个几何体共有几个面,每个面的三角形有何特点? (3)每个面的三角形面积为多少? 解1)如图,折起后的几何体是三棱锥 P(A,B.C) (2)这个几何体共有4个面,其中△DEF为等腰三角形,△PEF为等腰直角三角形,△DPE和 △DPF均为直角三角形 (3)SAPEF-d,SaDPF-SADPE-7X2axa-d, S0-rE-SaD-S0E(2a)--d--d 10.在长方体ABCD-A1B1C1D1中,AB=3,BC=2,BB1=1.求沿长方体的表面从点A到点C1的最 短距离 解如图,在长方体ABCD-A1B1CD1中AB=3,BC=-2,BB=l
8.下列说法正确的是 (填序号). ①棱柱的所有面都是四边形; ②一个棱柱至少有五个面; ③棱锥被平面分成的两部分不可能都是棱锥; ④棱柱被平面分成的两部分可以都是棱柱; ⑤棱台的上底面的面积与下底面的面积之比一定小于 1. 答案②④⑤ 解析①错误,棱柱的所有侧面都是平行四边形,而底面不一定是四边形;②正确;③错误,如图, 四棱锥被截面 PBD 分成的两部分都是棱锥;④正确;⑤正确,由棱台的定义知,棱台是由棱锥截 得的,截面是棱台的上底面,故上底面的面积一定小于下底面的面积. 9.如图,在边长为 2a 的正方形 ABCD 中,E,F 分别为 AB,BC 的中点,沿图中虚线将 3 个三角形 折起,使点 A,B,C 重合,重合后记为点 P.问: (1)折起后形成的几何体是什么几何体? (2)这个几何体共有几个面,每个面的三角形有何特点? (3)每个面的三角形面积为多少? 解(1)如图,折起后的几何体是三棱锥. (2)这个几何体共有 4 个面,其中△DEF 为等腰三角形,△PEF 为等腰直角三角形,△DPE 和 △DPF 均为直角三角形. (3)S△PEF= 1 2 a 2 ,S△DPF=S△DPE= 1 2 ×2a×a=a2 , S△DEF=S 正方形 ABCD-S△PEF-S△DPF-S△DPE=(2a) 2 - 1 2 a 2 -a 2 -a 2= 3 2 a 2 . 10.在长方体 ABCD-A1B1C1D1 中,AB=3,BC=2,BB1=1.求沿长方体的表面从点 A 到点 C1 的最 短距离. 解如图,在长方体 ABCD-A1B1C1D1 中,AB=3,BC=2,BB1=1

B 如图①,将侧面ABB1A1和侧面BCC1B1展开,则有AC1-V52+12=V26,即经过侧面ABB1M1 和侧面BCC1B1时的最短距离是V26; 如图②,将侧面ABB1A1和底面A1B1C1D1展开,则有AC1-V32+32-3VZ,即经过侧面ABB1A1 和底面A1B1C1D1时的最短距离是3VZ: 如图③,将侧面ADD141和底面A1B1C1D1展开,则有AC1=V√42+22=2V5,即经过侧面ADD1A1 和底面A1B1C1D1时的最短距离是2V5. 因为3V2<25,3vZ<v26, 所以沿长方体的表面从A到C1的最短距离为3√Z. D1 C C ① D A B ② B D A ③
如图①,将侧面 ABB1A1 和侧面 BCC1B1 展开,则有 AC1=√5 2 + 1 2 = √26,即经过侧面 ABB1A1 和侧面 BCC1B1 时的最短距离是√26; 如图②,将侧面 ABB1A1 和底面 A1B1C1D1 展开,则有 AC1=√3 2 + 3 2=3√2,即经过侧面 ABB1A1 和底面 A1B1C1D1 时的最短距离是 3√2; 如图③,将侧面 ADD1A1 和底面 A1B1C1D1 展开,则有 AC1=√4 2 + 2 2=2√5,即经过侧面 ADD1A1 和底面 A1B1C1D1 时的最短距离是 2√5. 因为 3√2<2√5,3√2 < √26, 所以沿长方体的表面从 A 到 C1 的最短距离为 3√2. ① ② ③