
第2课时平面与平面垂直的性质定理 课后·训练提升 基础巩固 1.设平面aL平面B,在平面a内的一条直线a垂直于平面B内的一条直线b,则(). A.直线a必垂直于平面B B.直线b必垂直于平面a C.直线a不一定垂直于平面B D.过a的平面与过b的平面垂直 答案 2.己知二面角-1-B是直二面角,m为直线,y为平面,则下列命题为真命题的是(). A.若mca,则m⊥BB.若m⊥a,则m∥B C.若m∥a,则m⊥BD.若y∥a则y⊥B 答案D 解桐对于A,若mca,则m与B相交或mCB或m∥B,故A错误; 对于B,若m⊥a则m∥B或mCB,故B错误; 对于C,若m∥a则m与B相交或mcB或m∥B,故C错误; 对于D,若y∥a则y⊥B,故D正确. 3.如图,平面PAD⊥平面ABCD,四边形ABCD为矩形,PA⊥AD,下列结论不正确的是(). A.PD⊥BD B.PD⊥CD C.PB⊥BC D.PA⊥BD 答案A 解桐因为PA⊥AD,平面PAD⊥平面ABCD,平面PADn平面ABCD=AD,PAC平面PAD,所以 PA⊥平面ABCD,所以PA⊥BD.故D正确.同理CD⊥平面PAD,所以PD⊥CD.故B正确.因 为PA⊥平面ABCD,所以PA⊥BC,又BC⊥AB,PA∩AB=A,所以BC⊥平面PAB,所以PB⊥BC 故C正确.若PD⊥BD,又PA⊥BD,PA∩PD=P,则BD⊥平面PAD,则BDL⊥AD,显然不成立,故 A不正确」 4.在三棱锥P-ABC中,PA=PB=√6,平面PAB⊥平面ABC,PA⊥PB,AB⊥BC,∠BAC=30°,则 PC=( A.V6 B.2V6 C.10 D.210 答案C 解析因为PA=PB=V6,PA⊥PB,所以AB=2V3 因为AB⊥BC,∠BAC-30° 所以BC=ABtan30°=2. 因为平面PAB⊥平面ABC,AB⊥BC,平面PABn平面ABC=AB,BCC平面ABC,所以BC⊥平面 PAB,所以BC⊥PB,所以PC=VPB2+BCz=V1O
第 2 课时 平面与平面垂直的性质定理 课后· 基础巩固 1.设平面 α⊥平面 β,在平面 α 内的一条直线 a 垂直于平面 β 内的一条直线 b,则( ). A.直线 a 必垂直于平面 β B.直线 b 必垂直于平面 α C.直线 a 不一定垂直于平面 β D.过 a 的平面与过 b 的平面垂直 答案 C 2.已知二面角 α-l-β 是直二面角,m 为直线,γ 为平面,则下列命题为真命题的是( ). A.若 m⊂α,则 m⊥β B.若 m⊥α,则 m∥β C.若 m∥α,则 m⊥β D.若 γ∥α,则 γ⊥β 答案 D 解析对于 A,若 m⊂α,则 m 与 β 相交或 m⊂β 或 m∥β,故 A 错误; 对于 B,若 m⊥α,则 m∥β 或 m⊂β,故 B 错误; 对于 C,若 m∥α,则 m 与 β 相交或 m⊂β 或 m∥β,故 C 错误; 对于 D,若 γ∥α,则 γ⊥β,故 D 正确. 3.如图,平面 PAD⊥平面 ABCD,四边形 ABCD 为矩形,PA⊥AD,下列结论不正确的是( ). A.PD⊥BD B.PD⊥CD C.PB⊥BC D.PA⊥BD 答案 A 解析因为 PA⊥AD,平面 PAD⊥平面 ABCD,平面 PAD∩平面 ABCD=AD,PA⊂平面 PAD,所以 PA⊥平面 ABCD,所以 PA⊥BD.故 D 正确.同理 CD⊥平面 PAD,所以 PD⊥CD.故 B 正确.因 为 PA⊥平面 ABCD,所以 PA⊥BC,又 BC⊥AB,PA∩AB=A,所以 BC⊥平面 PAB,所以 PB⊥BC. 故 C 正确.若 PD⊥BD,又 PA⊥BD,PA∩PD=P,则 BD⊥平面 PAD,则 BD⊥AD,显然不成立,故 A 不正确. 4.在三棱锥 P-ABC 中,PA=PB=√6,平面 PAB⊥平面 ABC,PA⊥PB,AB⊥BC,∠BAC=30°,则 PC=( ). A.√6 B.2√6 C.√10 D.2√10 答案 C 解析因为 PA=PB=√6,PA⊥PB,所以 AB=2√3. 因为 AB⊥BC,∠BAC=30°, 所以 BC=ABtan 30°=2. 因为平面 PAB⊥平面 ABC,AB⊥BC,平面 PAB∩平面 ABC=AB,BC⊂平面 ABC,所以 BC⊥平面 PAB,所以 BC⊥PB,所以 PC=√𝑃𝐵2 + 𝐵𝐶2 = √10
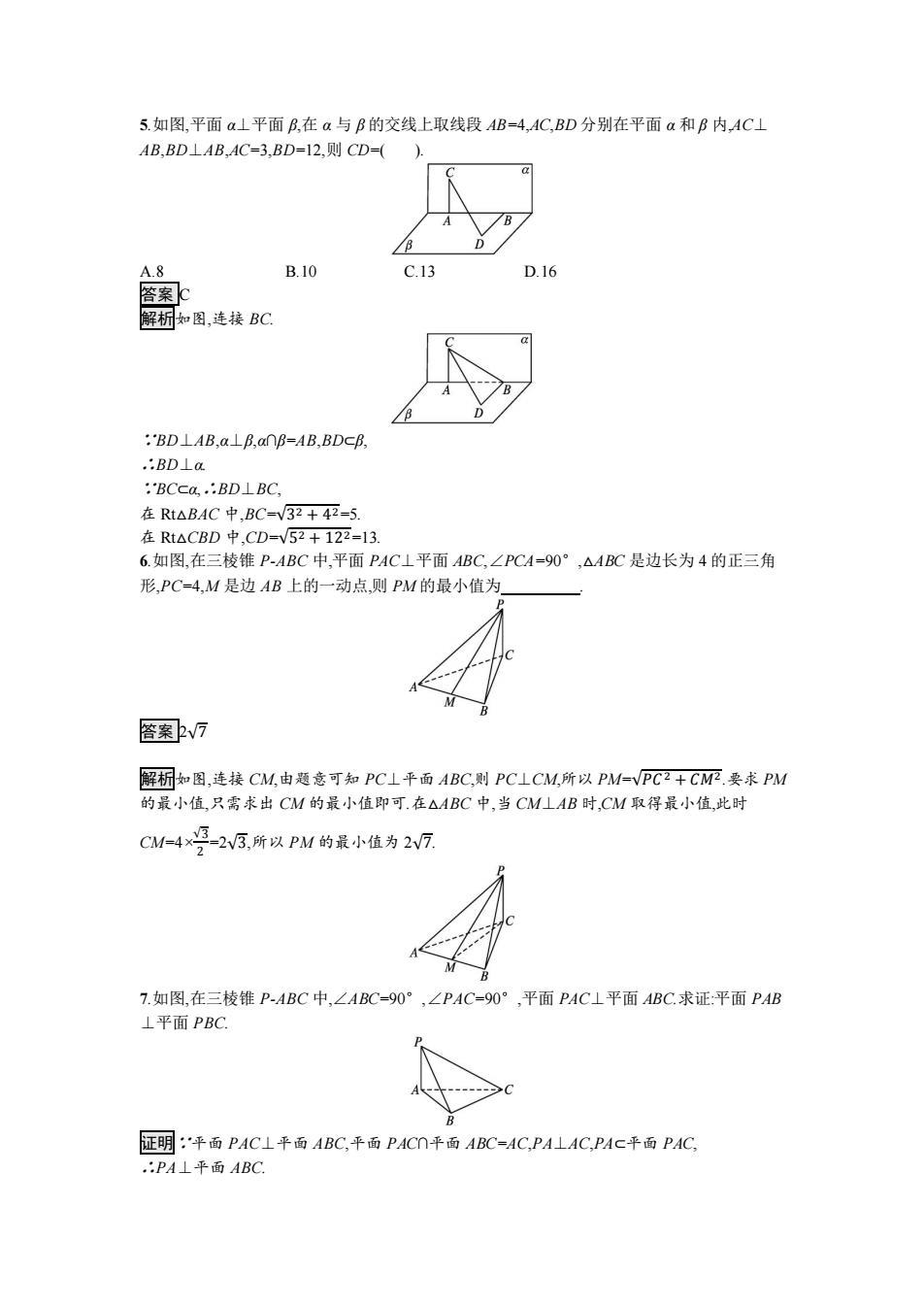
5.如图,平面a⊥平面B,在a与B的交线上取线段AB=4,AC,BD分别在平面a和B内,AC⊥ AB,BD⊥AB,AC=3,BD=12,则CD=( A.8 B.10 C.13 D.16 靥案c 解析如图,连接BC :BD⊥AB,a⊥PB,anB=AB,BDcf, :BD⊥a :BCca,:BD⊥BC 在Rt△BAC中,BC-V32+42-5. 在Rt△CBD中,CD-V52+122-13. 6.如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,∠PCA-90°,△4BC是边长为4的正三角 形,PC=4,M是边AB上的一动点,则PM的最小值为 含案v7 解析如图,连接CM,由题意可知PC⊥平面ABC,则PC⊥CM,所以PM=VPC2+CM要求PM 的最小值,只需求出CM的最小值即可.在△ABC中,当CMLAB时,CM取得最小值,此时 CM-4×号-2,所以PM的最小值为2V7. 7.如图,在三棱锥P-ABC中,∠ABC-90°,∠PAC=90°,平面PAC⊥平面ABC.求证:平面PAB ⊥平面PBC. 证明:平面PAC⊥平面ABC,平面PACn平面ABC-AC,PA⊥AC,PAc平面PAC .:PA⊥平面ABC
5.如图,平面 α⊥平面 β,在 α 与 β 的交线上取线段 AB=4,AC,BD 分别在平面 α 和 β 内,AC⊥ AB,BD⊥AB,AC=3,BD=12,则 CD=( ). A.8 B.10 C.13 D.16 答案 C 解析如图,连接 BC. ∵BD⊥AB,α⊥β,α∩β=AB,BD⊂β, ∴BD⊥α. ∵BC⊂α,∴BD⊥BC, 在 Rt△BAC 中,BC=√3 2 + 4 2=5. 在 Rt△CBD 中,CD=√5 2 + 12 2=13. 6.如图,在三棱锥 P-ABC 中,平面 PAC⊥平面 ABC,∠PCA=90°,△ABC 是边长为 4 的正三角 形,PC=4,M 是边 AB 上的一动点,则 PM 的最小值为 . 答案 2√7 解析如图,连接 CM,由题意可知 PC⊥平面 ABC,则 PC⊥CM,所以 PM=√𝑃𝐶2 + 𝐶𝑀2.要求 PM 的最小值,只需求出 CM 的最小值即可.在△ABC 中,当 CM⊥AB 时,CM 取得最小值,此时 CM=4× √3 2 =2√3,所以 PM 的最小值为 2√7. 7.如图,在三棱锥 P-ABC 中,∠ABC=90°,∠PAC=90°,平面 PAC⊥平面 ABC.求证:平面 PAB ⊥平面 PBC. 证明∵平面 PAC⊥平面 ABC,平面 PAC∩平面 ABC=AC,PA⊥AC,PA⊂平面 PAC, ∴PA⊥平面 ABC

又BCC平面ABC,:PA⊥BC 又AB⊥BC,4B0PA=A,:BC⊥平面PAB. 又BCC平面PBC,:平面PAB⊥平面PBC 8.如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90° AB=BC=PB=PC=2CD,侧面PBC⊥底面ABCD,则PA与BD是否相互垂直?请证明你的结论 D 解PA与BD互相垂直证明如下: 如图,取BC的中点O,连接PO,AO. :PB=PC,:PO⊥BC 又侧面PBC⊥底面ABCD,侧面PBCn底面ABCD=BC, .:POL底面ABCD .:PO⊥BD. :'AB=BC=2CD,..BO=CD. 又∠ABO=∠BCD=90°, .:AABO≌△BCD .:∠BAO=∠CBD 又∠CBD+∠ABD=90° :∠BAO+∠ABD-90°,:AO⊥BD. 又P0n40=0, .:BD⊥平面PAO .:BD⊥PA, :PA与BD相互垂直」 拓展提高 1.己知平面a⊥平面B,且平面a与平面B相交于直线1,直线aca,直线bcB,a,b与1不重合,则 下列结论错误的是() A.若a∥b则a∥1,b∥1 B.若a⊥b,则a⊥1,且b⊥1 C.若直线a,b都不平行于直线1,则直线a必不平行于直线b D.若直线a,b都不垂直于直线I,则直线a必不垂直于直线b 答案B 解析对于A,因为平面aL平面B,且平面a与平面B相交于直线l,aCa所以atp,又a∥ b,bcf,所以a∥B. 又平面a与平面B相交于直线I,aCa,所以a∥l,同理b∥l,故A正确
又 BC⊂平面 ABC,∴PA⊥BC. 又 AB⊥BC,AB∩PA=A,∴BC⊥平面 PAB. 又 BC⊂平面 PBC,∴平面 PAB⊥平面 PBC. 8.如图,已知四棱锥 P-ABCD 的底面是直角梯形,∠ABC=∠BCD=90°, AB=BC=PB=PC=2CD,侧面 PBC⊥底面 ABCD,则 PA 与 BD 是否相互垂直?请证明你的结论. 解 PA 与 BD 互相垂直.证明如下: 如图,取 BC 的中点 O,连接 PO,AO. ∵PB=PC,∴PO⊥BC. 又侧面 PBC⊥底面 ABCD,侧面 PBC∩底面 ABCD=BC, ∴PO⊥底面 ABCD, ∴PO⊥BD. ∵AB=BC=2CD,∴BO=CD. 又∠ABO=∠BCD=90°, ∴△ABO≌△BCD, ∴∠BAO=∠CBD. 又∠CBD+∠ABD=90°, ∴∠BAO+∠ABD=90°,∴AO⊥BD. 又 PO∩AO=O, ∴BD⊥平面 PAO, ∴BD⊥PA, ∴PA 与 BD 相互垂直. 拓展提高 1.已知平面 α⊥平面 β,且平面 α 与平面 β 相交于直线 l,直线 a⊂α,直线 b⊂β,a,b 与 l 不重合,则 下列结论错误的是( ). A.若 a∥b,则 a∥l,b∥l B.若 a⊥b,则 a⊥l,且 b⊥l C.若直线 a,b 都不平行于直线 l,则直线 a 必不平行于直线 b D.若直线 a,b 都不垂直于直线 l,则直线 a 必不垂直于直线 b 答案 B 解析对于 A,因为平面 α⊥平面 β,且平面 α 与平面 β 相交于直线 l,a⊂α,所以 a⊄β,又 a∥ b,b⊂β,所以 a∥β. 又平面 α 与平面 β 相交于直线 l,a⊂α,所以 a∥l,同理 b∥l,故 A 正确

对于B,若a⊥1,而平面a⊥平面B,平面a∩平面B=l,aca,则a⊥平面B,又bcB,则a⊥b一定成 立,但b与I不一定垂直,故B错误, 对于C,假设a∥b,由A可知a∥1,b∥1,与已知矛盾,故假设不成立,故C正确. 对于D,假设a⊥b,因为直线a,b都不垂直于直线I,所以在平面a内,存在直线c⊥l,且c与a 相交,根据面面垂直的性质定理,可知c⊥B,而bCB,所以c⊥b,而a⊥b,a与c相交,所以b⊥a, 又1Ca所以b⊥1,这与已知矛盾,故假设不成立,故D正确. 2.设m,n是两条不同的直线,aB是两个不同的平面,则(). A若a⊥B,canB=n,m⊥n,则m⊥a B.若a⊥B,m⊥B,则m∥a C.若a⊥B,m⊥B,n⊥a,则m⊥n D.若m⊥n,n⊥B,B⊥a,则m⊥a 答案c 3.己知三棱锥P-ABC的高为PH,若三个侧面两两垂直,则H为△ABC的(). A内心 B.外心 C.垂心 D.重心 答案 解析如图,由题意易知APL平面PBC 因为BCc平面PBC, 所以AP⊥BC 因为PH⊥平面ABC,BCC平面ABC, 所以PH⊥BC 又AP∩PH=P,所以BC⊥平面APH 又AHC平面APH,所以AH⊥BC 同理可得CH⊥AB 故H为△ABC的垂心 4.如图,P是菱形ABCD所在平面外的一点,且∠DAB=60°,AB的长为a.侧面PAD为正三角 形,其所在平面垂直于底面ABCD,PB与平面ABCD所成的角为O,则O= D 答案45° 解析如图,取AD的中点G,连接PG,BG,BD. G
对于 B,若 a⊥l,而平面 α⊥平面 β,平面 α∩平面 β=l,a⊂α,则 a⊥平面 β,又 b⊂β,则 a⊥b 一定成 立,但 b 与 l 不一定垂直,故 B 错误. 对于 C,假设 a∥b,由 A 可知 a∥l,b∥l,与已知矛盾,故假设不成立,故 C 正确. 对于 D,假设 a⊥b,因为直线 a,b 都不垂直于直线 l,所以在平面 α 内,存在直线 c⊥l,且 c 与 a 相交,根据面面垂直的性质定理,可知 c⊥β,而 b⊂β,所以 c⊥b,而 a⊥b,a 与 c 相交,所以 b⊥α, 又 l⊂α,所以 b⊥l,这与已知矛盾,故假设不成立,故 D 正确. 2.设 m,n 是两条不同的直线,α,β 是两个不同的平面,则( ). A.若 α⊥β,α∩β=n,m⊥n,则 m⊥α B.若 α⊥β,m⊥β,则 m∥α C.若 α⊥β,m⊥β,n⊥α,则 m⊥n D.若 m⊥n,n⊥β,β⊥α,则 m⊥α 答案 C 3.已知三棱锥 P-ABC 的高为 PH,若三个侧面两两垂直,则 H 为△ABC 的( ). A.内心 B.外心 C.垂心 D.重心 答案 C 解析如图,由题意易知 AP⊥平面 PBC. 因为 BC⊂平面 PBC, 所以 AP⊥BC. 因为 PH⊥平面 ABC,BC⊂平面 ABC, 所以 PH⊥BC. 又 AP∩PH=P,所以 BC⊥平面 APH. 又 AH⊂平面 APH,所以 AH⊥BC. 同理可得 CH⊥AB. 故 H 为△ABC 的垂心. 4.如图,P 是菱形 ABCD 所在平面外的一点,且∠DAB=60°,AB 的长为 a.侧面 PAD 为正三角 形,其所在平面垂直于底面 ABCD,PB 与平面 ABCD 所成的角为 θ,则 θ= . 答案 45° 解析如图,取 AD 的中点 G,连接 PG,BG,BD
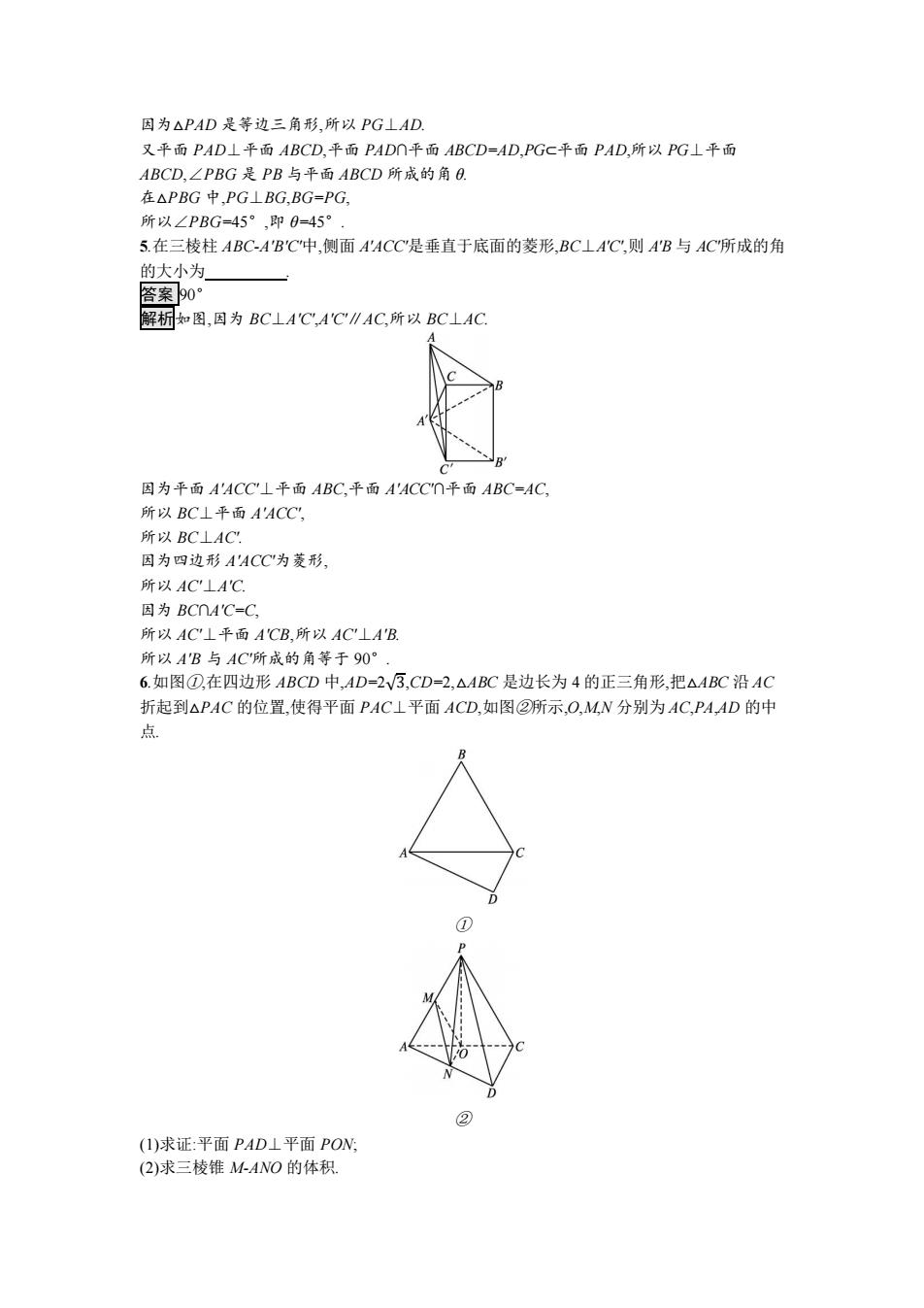
因为△PAD是等边三角形,所以PGLAD. 又平面PAD⊥平面ABCD,平面PADn平面ABCD=AD,PGC平面PAD,所以PG⊥平面 ABCD,∠PBG是PB与平面ABCD所成的角O. 在△PBG中,PG⊥BG,BG=PG, 所以∠PBG=45°,即0=45° 5.在三棱柱ABC-AB'C中,侧面AACC"是垂直于底面的菱形,BCLAC',则A'B与AC所成的角 的大小为 答案90° 解析如图,因为BC⊥A'C',A'C∥AC,所以BC⊥AC 因为平面AACC⊥平面ABC,平面4'ACCn平面ABC=AC, 所以BC⊥平面A'ACC, 所以BC⊥AC 因为四边形A'ACC为菱形, 所以AC⊥A'C 因为BCnA'C=C 所以AC⊥平面A'CB,所以AC'⊥A'B. 所以AB与AC所成的角等于90°. 6.如图①,在四边形ABCD中,AD=2√3,CD=2,△ABC是边长为4的正三角形,把△ABC沿AC 折起到△PAC的位置,使得平面PAC⊥平面ACD,如图②所示,O,MN分别为AC,PA,AD的中 点 (1)求证:平面PAD⊥平面POW: (2)求三棱锥M-ANO的体积
因为△PAD 是等边三角形,所以 PG⊥AD. 又平面 PAD⊥平面 ABCD,平面 PAD∩平面 ABCD=AD,PG⊂平面 PAD,所以 PG⊥平面 ABCD,∠PBG 是 PB 与平面 ABCD 所成的角 θ. 在△PBG 中,PG⊥BG,BG=PG, 所以∠PBG=45°,即 θ=45°. 5.在三棱柱 ABC-A'B'C'中,侧面 A'ACC'是垂直于底面的菱形,BC⊥A'C',则 A'B 与 AC'所成的角 的大小为 . 答案 90° 解析如图,因为 BC⊥A'C',A'C'∥AC,所以 BC⊥AC. 因为平面 A'ACC'⊥平面 ABC,平面 A'ACC'∩平面 ABC=AC, 所以 BC⊥平面 A'ACC', 所以 BC⊥AC'. 因为四边形 A'ACC'为菱形, 所以 AC'⊥A'C. 因为 BC∩A'C=C, 所以 AC'⊥平面 A'CB,所以 AC'⊥A'B. 所以 A'B 与 AC'所成的角等于 90°. 6.如图①,在四边形 ABCD 中,AD=2√3,CD=2,△ABC 是边长为 4 的正三角形,把△ABC 沿 AC 折起到△PAC 的位置,使得平面 PAC⊥平面 ACD,如图②所示,O,M,N 分别为 AC,PA,AD 的中 点. ① ② (1)求证:平面 PAD⊥平面 PON; (2)求三棱锥 M-ANO 的体积

(1证明因为△PAC为正三角形,O为AC的中点,所以PO⊥AC. 又平面PAC⊥平面ACD,平面PACn平面ACD=AC,所以PO⊥平面ACD. 又ADC平面ACD,所以PO⊥AD 因为AD=23,CD=2,AC=4, 所以AD2+CD2=AC2,所以AD⊥CD 又O,N分别为AC,AD的中点, 所以ON∥CD,所以AD⊥ON 又ONOPO=O,所以AD⊥平面PON. 又ADc平面PAD,所以平面PAD⊥平面PON (2解国为△PAC是边长为4的等边三角形, 所以P0=2v3 又POL平面ACD,M为PA的中点,所以M到平面ACD的距离d-P0=V3 因为ON为△1CD的中位线,所以S0Nam-×x232号 所以n4oord×9xV万=号 挑战创新 如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,PA⊥AB,AB∥CD,∠ DAB=90°,PA=AD,DC=2AB. 求证:(I)PA⊥BC (2)平面PBC⊥平面PDC. 证明1)因为平面PAB⊥平面ABCD, 平面PAB∩平面ABCD=AB,PA⊥AB, PAC平面PAB,所以PA⊥平面ABCD, 又BCC平面ABCD.所以PA⊥BC (2)取PC的中点E,PD的中点F 连接BE,AF,EF(图略), 剥EF∥CD,EF-CD 又AB∥CD,ABCD,所以EFAB. 所以四边形ABEF为平行四边形,所以BE∥AF 因为PA=AD,F为PD的中点,所以AF⊥PD. 由(I)知PA⊥平面ABCD,所以PA⊥CD. 又∠DAB-90°,AB∥CD,所以CD⊥AD 又PAMAD=A,所以CD⊥平面PAD, 所以CD⊥AF
(1)证明因为△PAC 为正三角形,O 为 AC 的中点,所以 PO⊥AC. 又平面 PAC⊥平面 ACD,平面 PAC∩平面 ACD=AC,所以 PO⊥平面 ACD. 又 AD⊂平面 ACD,所以 PO⊥AD. 因为 AD=2√3,CD=2,AC=4, 所以 AD2+CD2=AC2 ,所以 AD⊥CD. 又 O,N 分别为 AC,AD 的中点, 所以 ON∥CD,所以 AD⊥ON. 又 ON∩PO=O,所以 AD⊥平面 PON. 又 AD⊂平面 PAD,所以平面 PAD⊥平面 PON. (2)解因为△PAC 是边长为 4 的等边三角形, 所以 PO=2√3. 又 PO⊥平面 ACD,M 为 PA 的中点,所以 M 到平面 ACD 的距离 d=1 2 PO=√3. 因为 ON 为△ACD 的中位线,所以 S△AON= 1 4 S△ACD= 1 4 × 1 2 ×2√3×2= √3 2 . 所以 VM -ANO= 1 3 S△AON·d=1 3 × √3 2 × √3 = 1 2 . 挑战创新 如图,在四棱锥 P-ABCD 中,平面 PAB⊥平面 ABCD,PA⊥AB,AB∥CD,∠ DAB=90°,PA=AD,DC=2AB. 求证:(1)PA⊥BC; (2)平面 PBC⊥平面 PDC. 证明(1)因为平面 PAB⊥平面 ABCD, 平面 PAB∩平面 ABCD=AB,PA⊥AB, PA⊂平面 PAB,所以 PA⊥平面 ABCD. 又 BC⊂平面 ABCD,所以 PA⊥BC. (2)取 PC 的中点 E,PD 的中点 F, 连接 BE,AF,EF(图略), 则 EF∥CD,EF=1 2 CD. 又 AB∥CD,AB=1 2 CD,所以 EF AB. 所以四边形 ABEF 为平行四边形,所以 BE∥AF. 因为 PA=AD,F 为 PD 的中点,所以 AF⊥PD. 由(1)知 PA⊥平面 ABCD,所以 PA⊥CD. 又∠DAB=90°,AB∥CD,所以 CD⊥AD. 又 PA∩AD=A,所以 CD⊥平面 PAD, 所以 CD⊥AF

又PDNCD=D, 所以AF⊥平面PDC,所以BE⊥平面PDC 又BEC平面PBC,所以平面PBC⊥平面PDC
又 PD∩CD=D, 所以 AF⊥平面 PDC,所以 BE⊥平面 PDC. 又 BE⊂平面 PBC,所以平面 PBC⊥平面 PDC