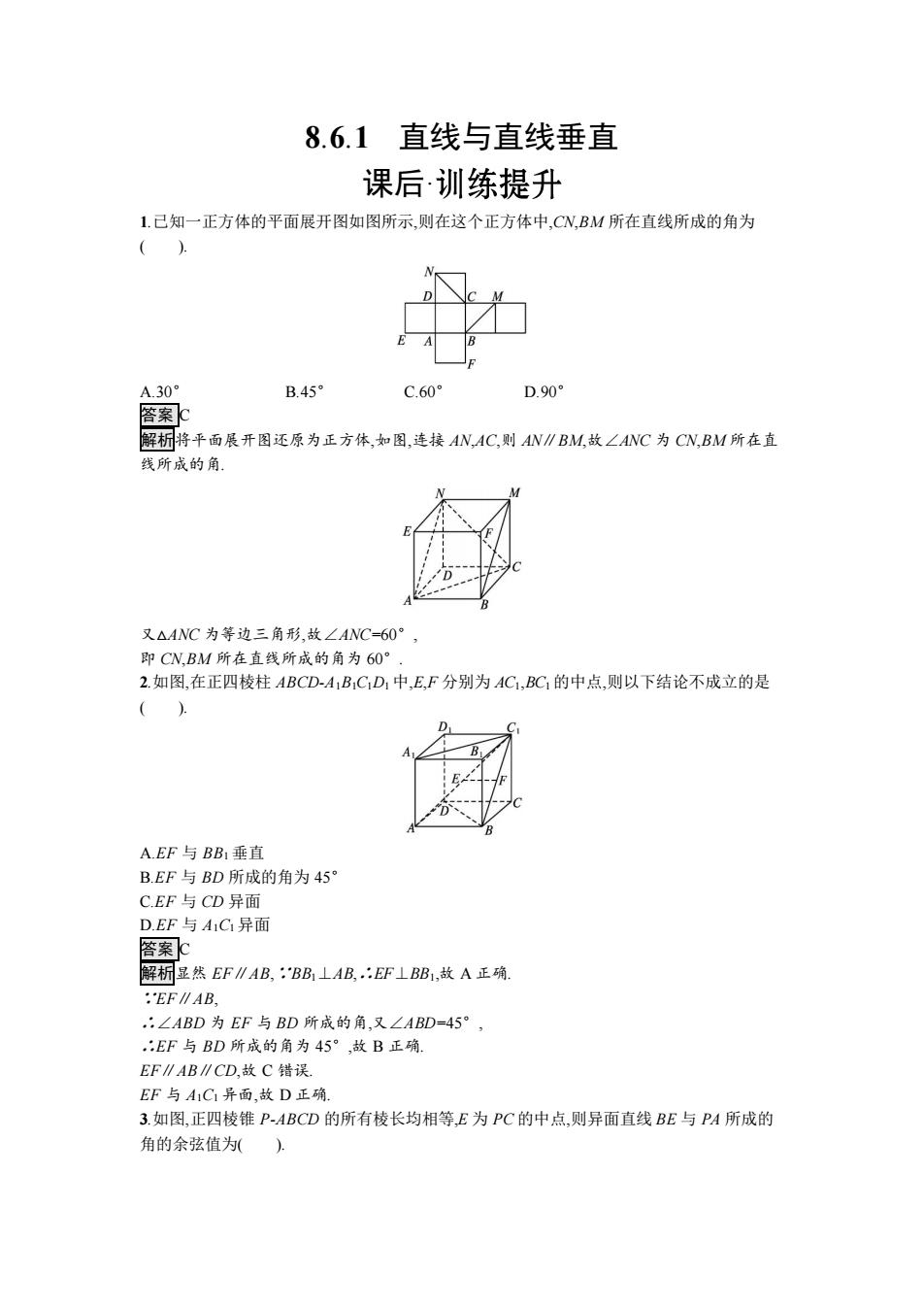
8.6.1直线与直线垂直 课后·训练提升 1.己知一正方体的平面展开图如图所示,则在这个正方体中,CN,BM所在直线所成的角为 ( A.30° B.45° C.60° D.90 答案 解析将平面展开图还原为正方体,如图,连接AN,AC,则AWN∥BM,故∠ANC为CN,BM所在直 线所成的角 又△4NC为等边三角形,故∠ANC=60°, 即CN,BM所在直线所成的角为60° 2.如图,在正四棱柱ABCD-A1B1CD,中,E,F分别为AC1,BC1的中点,则以下结论不成立的是 () A.EF与BB1垂直 B.EF与BD所成的角为45° C.EF与CD异面 D.EF与A1C异面 客案 解析显然EF∥AB,:BB⊥AB,:EF⊥BB1,故A正确 :EF∥AB, :∠ABD为EF与BD所成的角,又∠ABD=45°, :EF与BD所成的角为45°,故B正确. EF∥AB∥CD,故C错误. EF与A1C1异面,故D正确」 3.如图,正四棱锥P-ABCD的所有棱长均相等,E为PC的中点,则异面直线BE与PA所成的 角的余弦值为)
8.6.1 直线与直线垂直 课后· 1.已知一正方体的平面展开图如图所示,则在这个正方体中,CN,BM 所在直线所成的角为 ( ). A.30° B.45° C.60° D.90° 答案 C 解析将平面展开图还原为正方体,如图,连接 AN,AC,则 AN∥BM,故∠ANC 为 CN,BM 所在直 线所成的角. 又△ANC 为等边三角形,故∠ANC=60°, 即 CN,BM 所在直线所成的角为 60°. 2.如图,在正四棱柱 ABCD-A1B1C1D1 中,E,F 分别为 AC1,BC1 的中点,则以下结论不成立的是 ( ). A.EF 与 BB1 垂直 B.EF 与 BD 所成的角为 45° C.EF 与 CD 异面 D.EF 与 A1C1 异面 答案 C 解析显然 EF∥AB,∵BB1⊥AB,∴EF⊥BB1,故 A 正确. ∵EF∥AB, ∴∠ABD 为 EF 与 BD 所成的角,又∠ABD=45°, ∴EF 与 BD 所成的角为 45°,故 B 正确. EF∥AB∥CD,故 C 错误. EF 与 A1C1 异面,故 D 正确. 3.如图,正四棱锥 P-ABCD 的所有棱长均相等,E 为 PC 的中点,则异面直线 BE 与 PA 所成的 角的余弦值为( )
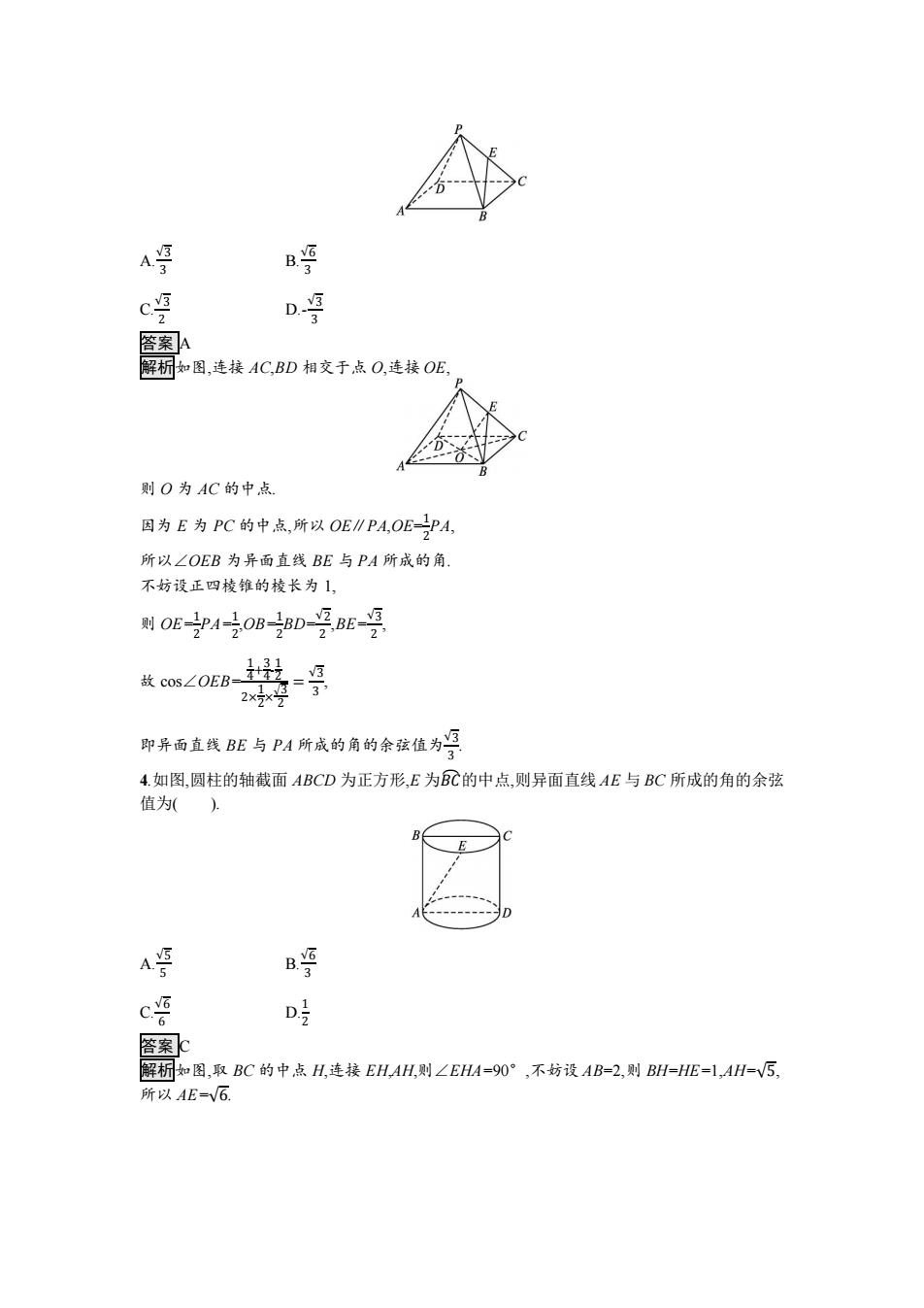
A号 B c兽 D 3 客案A 解桐如图,连接AC,BD相交于点O,连接OE, 则O为AC的中点 因为E为PC的中点,所以OE∥PA,OE-PA, 所以∠OEB为异面直线BE与PA所成的角. 不妨设正四棱锥的棱长为1, 则oE-A0B-BD-号BE-月 7 故s∠0EB-线- 2×2*号 3 即异面直线BE与PA所成的角的余弦值为 4.如图,圆柱的轴截面ABCD为正方形,E为BC的中点,则异面直线AE与BC所成的角的余弦 值为(). A B号 c唔 D 答案 解桐如图,取BC的中点H,连接EHAH,则∠EHA=90°,不妨设AB=2,则BH=HE=l,AH=V5, 所以AE=V6
A. √3 3 B. √6 3 C. √3 2 D.- √3 3 答案 A 解析如图,连接 AC,BD 相交于点 O,连接 OE, 则 O 为 AC 的中点. 因为 E 为 PC 的中点,所以 OE∥PA,OE=1 2 PA, 所以∠OEB 为异面直线 BE 与 PA 所成的角. 不妨设正四棱锥的棱长为 1, 则 OE=1 2 PA=1 2 ,OB=1 2 BD=√2 2 ,BE=√3 2 , 故 cos∠OEB= 1 4 + 3 4 - 1 2 2× 1 2 × √3 2 = √3 3 , 即异面直线 BE 与 PA 所成的角的余弦值为√3 3 . 4.如图,圆柱的轴截面 ABCD 为正方形,E 为𝐵𝐶⏜的中点,则异面直线 AE 与 BC 所成的角的余弦 值为( ). A. √5 5 B. √6 3 C. √6 6 D. 1 2 答案 C 解析如图,取 BC 的中点 H,连接 EH,AH,则∠EHA=90°,不妨设 AB=2,则 BH=HE=1,AH=√5, 所以 AE=√6

连接ED,则ED=√6 因为BC∥AD,所以∠EAD为异面直线AE与BC所成的角. 在△EAD中,eas∠EADZ装=吾 5.在正方体ABCD-A1B1C1D1中,点P在线段AD1上运动,则异面直线CP与BA1所成的角0的 取值范围是( A.0°<0<60° B.0°≤0<60° C.0°≤0≤60° D.0°<0≤60° 答案D 解析如图,连接CD1,AC,因为CD1∥BA1,所以CP与BA1所成的角就是CP与CD1所成的角 即0=∠D1CP 当点P从D1向A运动时,∠DCP从0°增大到60°,但当点P与D1重合时,CP∥BA1,这和 CP与BA1为异面直线矛盾,所以异面直线CP与BA1所成的角O的取值范围是 0°<0≤60°. 6.(多选题)如图,在空间四边形ABCD中,AB=CD,且AB与CD所成的角为30°,E,F分别为 BC,AD的中点,则EF与AB所成的角的大小可以是( A.15° B.30° C.60° D.75° 答案AD 解杨取AC的中点G,连接EG,FG,则EG∥AB且EGAB,FG∥CD且FGCD,由AB=CD 知EG=FG
连接 ED,则 ED=√6. 因为 BC∥AD,所以∠EAD 为异面直线 AE 与 BC 所成的角. 在△EAD 中,cos∠EAD= 6+4-6 2×2×√6 = √6 6 . 5.在正方体 ABCD-A1B1C1D1 中,点 P 在线段 AD1 上运动,则异面直线 CP 与 BA1 所成的角 θ 的 取值范围是( ). A.0°<θ<60° B.0°≤θ<60° C.0°≤θ≤60° D.0°<θ≤60° 答案 D 解析如图,连接 CD1,AC,因为 CD1∥BA1,所以 CP 与 BA1 所成的角就是 CP 与 CD1 所成的角, 即 θ=∠D1CP. 当点 P 从 D1 向 A 运动时,∠D1CP 从 0°增大到 60°,但当点 P 与 D1 重合时,CP∥BA1,这和 CP 与 BA1 为异面直线矛盾,所以异面直线 CP 与 BA1 所成的角 θ 的取值范围是 0°<θ≤60°. 6.(多选题)如图,在空间四边形 ABCD 中,AB=CD,且 AB 与 CD 所成的角为 30°,E,F 分别为 BC,AD 的中点,则 EF 与 AB 所成的角的大小可以是( ). A.15° B.30° C.60° D.75° 答案 AD 解析取 AC 的中点 G,连接 EG,FG,则 EG∥AB 且 EG=1 2 AB,FG∥CD 且 FG=1 2 CD,由 AB=CD 知 EG=FG

易知∠GEF(或它的补角)为EF与AB所成的角,∠EGF(或它的补角)为AB与CD所成的角. :AB与CD所成的角为30°, .:∠EGF=30°或150°. 由EG=FG知△EFG为等腰三角形, 当∠EGF-30°时,∠GEF-75°; 当∠EGF=150°时,∠GEF=15° 故EF与AB所成的角为15°或75° 7.如图,空间四边形ABCD的对角线AC=8,BD=6,M,N分别为AB,CD的中点,并且异面直线 AC与BD所成的角为90°,则MN等于 含案5 解析取AD的中点P,连接PM,PN,则BD∥PMAC∥PN, ,:∠MPN为异面直线AC与BD所成的角, ∠MPN=90°,PN2AC=4,PM-2BD=3 .MW=5. 8.如图,在正三棱柱ABC-A'B'C中,D为AB的中点,AC=A'A=2,求证:CD LAB, 证明如图,取BB的中点E,连接DE,CE
易知∠GEF(或它的补角)为 EF 与 AB 所成的角,∠EGF(或它的补角)为 AB 与 CD 所成的角. ∵AB 与 CD 所成的角为 30°, ∴∠EGF=30°或 150°. 由 EG=FG 知△EFG 为等腰三角形, 当∠EGF=30°时,∠GEF=75°; 当∠EGF=150°时,∠GEF=15°. 故 EF 与 AB 所成的角为 15°或 75°. 7.如图,空间四边形 ABCD 的对角线 AC=8,BD=6,M,N 分别为 AB,CD 的中点,并且异面直线 AC 与 BD 所成的角为 90°,则 MN 等于 . 答案 5 解析取 AD 的中点 P,连接 PM,PN,则 BD∥PM,AC∥PN, ∴∠MPN 为异面直线 AC 与 BD 所成的角, ∴∠MPN=90°,PN=1 2 AC=4,PM=1 2 BD=3, ∴MN=5. 8.如图,在正三棱柱 ABC -A'B'C'中,D 为 AB 的中点,AC=A'A=2,求证:CD⊥AB'. 证明如图,取 BB'的中点 E,连接 DE,CE

因为D为AB的中点,E为BB'的中点,所以DE∥AB,所以∠CDE为异面直线CD与AB所成 的角(或其补角),因为AC=A'A=2,所以DE=√2,CD=√3,CE=V5.因为CE2=CD+DE2,所以∠ CDE=90°.所以异面直线CD与AB所成的角为90°,即CD⊥AB 9.如图,在四棱柱ABCD-A1B1CD1中,侧面都是矩形,底面ABCD是菱形,且AB=BC-2V3,∠ ABC=120°,A1B⊥AD1,求A41的值 厨如图,连接CD,4C,在四棱柱ABCD-AB1CD1中, 因为A1D1∥BC,A1D1=BC, 所以四边形A1BCD1为平行四边形, 所以AB∥CD1, 所以∠ADC(或其补角)为A1B与AD1所成的角. 又A1B⊥AD1, 所以异面直线A1B与AD1所成的角为90°, 所以∠AD1C=90°. 由题意可知,四棱柱ABCD-A1B1CD1为直四棱柱,又AB=BC, 所以△ACD1为等腰直角三角形, 所以40,94C 因为AB=BC=2V3,∠ABC=120°, 所以AC-2V3×sin60°×2-6, 所以4D,停4C-3V2 所以A41-VAD-A1D=、J(3V22(2V3}2=V6. 10.如图,在正方体ABCD-A1B1C1D1中,O为AC的中点
因为 D 为 AB 的中点,E 为 BB'的中点,所以 DE∥AB',所以∠CDE 为异面直线 CD 与 AB'所成 的角(或其补角),因为 AC=A'A=2,所以 DE=√2,CD=√3,CE=√5.因为 CE2=CD2+DE2 ,所以∠ CDE=90°.所以异面直线 CD 与 AB'所成的角为 90°,即 CD⊥AB'. 9.如图,在四棱柱 ABCD-A1B1C1D1 中,侧面都是矩形,底面 ABCD 是菱形,且 AB=BC=2√3,∠ ABC=120°,A1B⊥AD1,求 AA1 的值. 解如图,连接 CD1,AC,在四棱柱 ABCD-A1B1C1D1 中, 因为 A1D1∥BC,A1D1=BC, 所以四边形 A1BCD1 为平行四边形, 所以 A1B∥CD1, 所以∠AD1C(或其补角)为 A1B 与 AD1 所成的角. 又 A1B⊥AD1, 所以异面直线 A1B 与 AD1 所成的角为 90°, 所以∠AD1C=90°. 由题意可知,四棱柱 ABCD-A1B1C1D1 为直四棱柱,又 AB=BC, 所以△ACD1 为等腰直角三角形, 所以 AD1= √2 2 AC. 因为 AB=BC=2√3,∠ABC=120°, 所以 AC=2√3×sin 60°×2=6, 所以 AD1= √2 2 AC=3√2, 所以 AA1=√𝐴𝐷1 2 -𝐴1𝐷1 2 = √(3√2) 2 -(2√3) 2 = √6. 10.如图,在正方体 ABCD-A1B1C1D1 中,O 为 AC 的中点

(1)求证:AD1∥平面DOC. (2)求异面直线AD1和OC所成的角的大小 (1证明如图,连接D1C交DC1于点O1,连接OO1 D 因为O,O1分别为AC,D1C的中点,所以OO1∥AD1. 又OO1C平面DOC1,AD1¢平面DOC1,所以AD1∥平面DOC1. (2解由(1)知,O01∥AD1, 所以∠O1OC1为异面直线AD1和OC1所成的角, 不妨设正方体ABCD-A1B1C1D1的棱长为2, 则01C=001=VZ,0C1-V6, 所以cos∠0,0C,26_ 2×V2×V6 2 所以∠0,0C音 即异面直线AD和OC所成的角的大小为铝 11.如图,在空间四边形ABCD中,AD,BC成60°的角,且AD=BC=a,平行于AD与BC的截面 分别交AB,AC,CD,BD于点E,F,G,H当点E在AB的何处时,截面EFGH的面积最大?最大面 积是多少? ☑:AD与BC成60°角, :∠HGF=60°或120°. 设AE:AB=x剥凭-岩- 又BC=a,.:EF=ar. 器=器1x得EH=a1-0 Saw8ow-=EFin60-ral-是=月r(er+-6+
(1)求证:AD1∥平面 DOC1. (2)求异面直线 AD1 和 OC1 所成的角的大小. (1)证明如图,连接 D1C 交 DC1 于点 O1,连接 OO1. 因为 O,O1 分别为 AC,D1C 的中点,所以 OO1∥AD1. 又 OO1⊂平面 DOC1,AD1⊄平面 DOC1,所以 AD1∥平面 DOC1. (2)解由(1)知,OO1∥AD1, 所以∠O1OC1 为异面直线 AD1 和 OC1 所成的角, 不妨设正方体 ABCD-A1B1C1D1 的棱长为 2, 则 O1C1=OO1=√2,OC1=√6, 所以 cos∠O1OC1= (√2) 2+(√6) 2 -(√2) 2 2×√2×√6 = √3 2 , 所以∠O1OC1= π 6 , 即异面直线 AD1 和 OC1 所成的角的大小为π 6 . 11.如图,在空间四边形 ABCD 中,AD,BC 成 60°的角,且 AD=BC=a,平行于 AD 与 BC 的截面 分别交 AB,AC,CD,BD 于点 E,F,G,H.当点 E 在 AB 的何处时,截面 EFGH 的面积最大?最大面 积是多少? 解∵AD 与 BC 成 60°角, ∴∠HGF=60°或 120°. 设 AE∶AB=x,则 𝐸𝐹 𝐵𝐶 = 𝐴𝐸 𝐴𝐵=x. 又 BC=a,∴EF=ax. 由 𝐸𝐻 𝐴𝐷 = 𝐵𝐸 𝐴𝐵=1-x,得 EH=a(1-x). ∴S 四边形 EFGH=EF·EH·sin 60°=ax·a(1-x)· √3 2 = √3 2 a 2 (-x 2+x)= √3 2 a 2 [-(x- 1 2 ) 2+ 1 4 ]

当x封,S2,即当E为AB的中点时藏面的面积最大,最大面积为
当 x= 1 2时,S 最大值= √3 8 a 2 ,即当 E 为 AB 的中点时,截面的面积最大,最大面积为√3 8 a 2