
7.4.1二项分布 一、教材分析 本节课选自《2019人教A版高中数学选择性必修第三册》,第七章《随机变量及其分布列》, 本节课主本节课主要学习二项分布 二、学情分析 前面学生己经掌握了有关概率的基础知识等可能事件概率、互斥事件概率、条件概率和相互独 立事件概率的求法、也学习了分布列的有关内容。二项分布是一种应用广泛的概率模型,是对前面 所学知识的综合应用。节课是从实际出发,通过抽象思维,建立数学模型,进而认知数学理论,应 用于实际的过程。 三、教学目标 课程目标 学科素养 A.理解伯努利试验以及n重伯努利试验的 1.数学抽象:n重伯努利试验的概念 概念,掌握随机变量服从二项分布的有关 2逻辑推理:二项分布的随机变量的均值和方差 计算 3数学运算:二项分布的有关计算 B.能够解决随机变量服从二项分布的实际 4数学建模:模型化思想 应用问题,会求服从二项分布的随机变量 的均值和方差 四、教学重难点 重点:n重伯努利实验,二项分布及其数字特征: 难点:在实际问题中抽象出模型的特征,识别二项分布 五、课前准备 (一)学习资源 (二)学习任务单 (三)教学方法及工具:以学生为主体,小组为单位,采用诱思探究式教学,精讲多练。 多媒体。 六、教学过程 一、问题导学 随机 是否为n重伯 伯务利试验 P 重复试验 试验 努利试验 A) 的次数 是 抛掷一枚质地均匀 0.5 10 的硬币
7.4.1 二项分布 一、教材分析 本节课选自《2019 人教 A 版高中数学选择性必修第三册》,第七章《随机变量及其分布列》, 本节课主本节课主要学习二项分布 二、学情分析 前面学生已经掌握了有关概率的基础知识等可能事件概率、互斥事件概率、条件概率和相互独 立事件概率的求法、也学习了分布列的有关内容。二项分布是一种应用广泛的概率模型,是对前面 所学知识的综合应用。节课是从实际出发,通过抽象思维,建立数学模型,进而认知数学理论,应 用于实际的过程。 三、教学目标 课程目标 学科素养 A.理解伯努利试验以及 n 重伯努利试验的 概念,掌握随机变量服从二项分布的有关 计算; B.能够解决随机变量服从二项分布的实际 应用问题,会求服从二项分布的随机变量 的均值和方差. 1.数学抽象:n 重伯努利试验的概念 2.逻辑推理: 二项分布的随机变量的均值和方差 3.数学运算:二项分布的有关计算 4.数学建模:模型化思想 四、教学重难点 重点:n 重伯努利实验,二项分布及其数字特征; 难点:在实际问题中抽象出模型的特征,识别二项分布. 五、课前准备 (一)学习资源 (二)学习任务单 (三)教学方法及工具:以学生为主体,小组为单位,采用诱思探究式教学,精讲多练。 多媒体。 六、教学过程 一、 问题导学 随机 试验 是否为 n 重伯 努利试验 伯努利试验 P( A) 重复试验 的次数 1 是 抛掷一枚质地均匀 的硬币 0.5 10
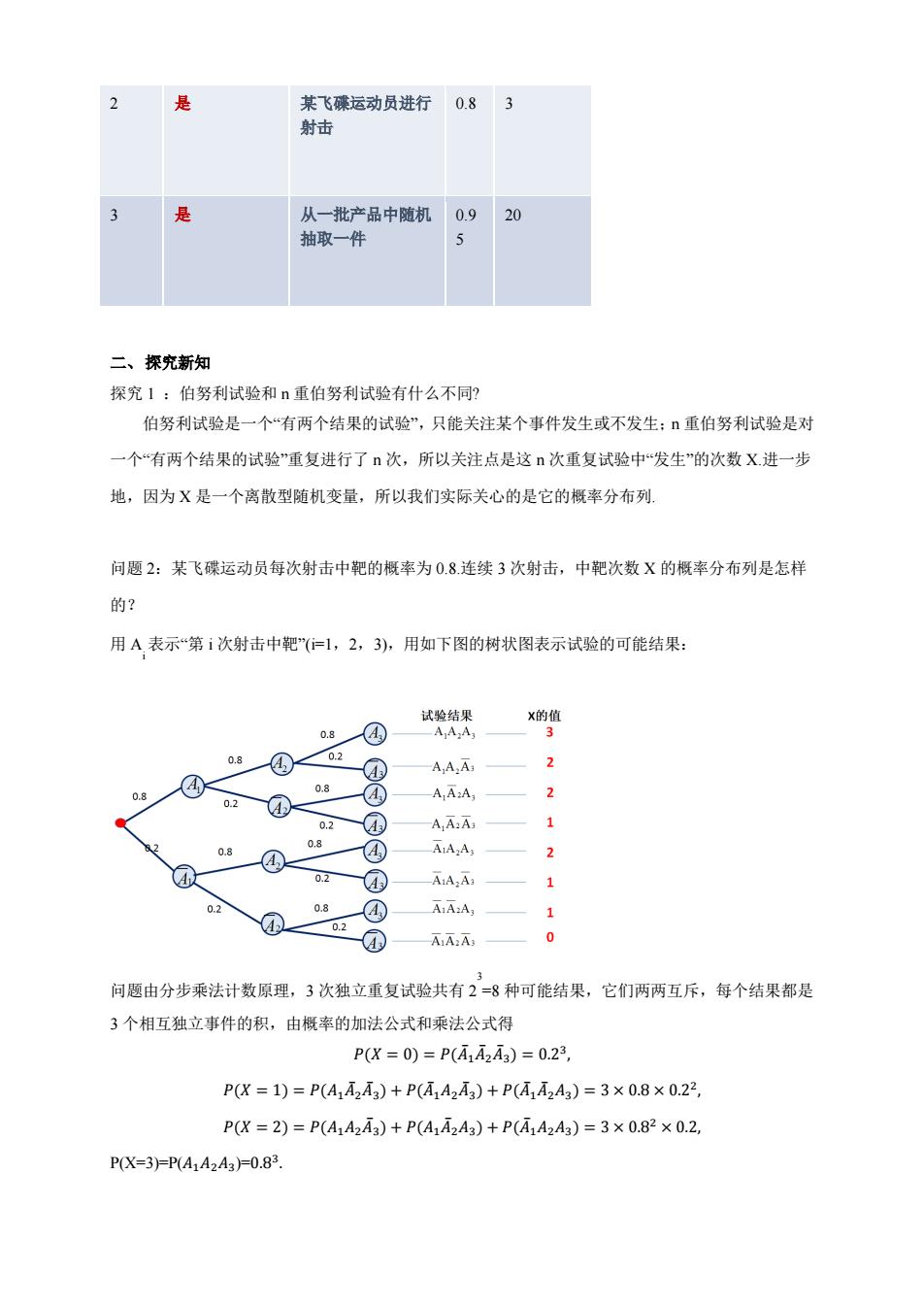
某飞碟运动员进行 0.8 射击 是 从一批产品中随机 0.9 20 抽取一件 5 二、探究新知 探究1:伯努利试验和n重伯努利试验有什么不同? 伯努利试验是一个“有两个结果的试验”,只能关注某个事件发生或不发生:重伯努利试验是对 一个“有两个结果的试验”重复进行了n次,所以关注点是这n次重复试验中“发生”的次数X进一步 地,因为X是一个离散型随机变量,所以我们实际关心的是它的概率分布列 问题2:某飞碟运动员每次射击中靶的概率为0.8连续3次射击,中靶次数X的概率分布列是怎样 的? 用A表示“第i次射击中靶”(=1,2,3),用如下图的树状图表示试验的可能结果: 试验结果 X的值 0.8 ④ -AAA3 0.8 ④ 0.2 ④ A,A:A 0.8 ④ 0.8 ④ AAA, 2 0.2 @ AA2A 1 w 0.8 ④ ④ AA2A 2 0.2 @ AA2A3 0.2 0.8 ④ AA2A3 A 0.2 @ AA2A3 0 问题由分步乘法计数原理,3次独立重复试验共有2=8种可能结果,它们两两互斥,每个结果都是 3个相互独立事件的积,由概率的加法公式和乘法公式得 P(X=0)=P(A1A2A3)=0.23, P(X=1)=P(A1A2A3)+P(A1A2A3)+P(A1A2A3)=3×0.8×0.22, P(X=2)=P(A1A2A3)+P(A1A2A3)+P(A1A2A3)=3×0.82×0.2, PX=3)=P(A1A2A3)=0.83
2 是 某飞碟运动员进行 射击 0.8 3 3 是 从一批产品中随机 抽取一件 0.9 5 20 二、 探究新知 探究 1 :伯努利试验和 n 重伯努利试验有什么不同? 伯努利试验是一个“有两个结果的试验”,只能关注某个事件发生或不发生;n 重伯努利试验是对 一个“有两个结果的试验”重复进行了 n 次,所以关注点是这 n 次重复试验中“发生”的次数 X.进一步 地,因为 X 是一个离散型随机变量,所以我们实际关心的是它的概率分布列. 问题 2:某飞碟运动员每次射击中靶的概率为 0.8.连续 3 次射击,中靶次数 X 的概率分布列是怎样 的? 用 A i 表示“第 i 次射击中靶”(i=1,2,3),用如下图的树状图表示试验的可能结果: 问题由分步乘法计数原理,3 次独立重复试验共有 2 3 =8 种可能结果,它们两两互斥,每个结果都是 3 个相互独立事件的积,由概率的加法公式和乘法公式得 ̅ ̅ ̅ ̅ ̅ ̅ ̅ ̅ ̅ ̅ ̅ ̅ P(X=3)=P( )=

为了简化表示,每次射击用1表示中靶,用0表示脱靶,那么3次射击恰好2次中靶的所有可能结 果可表示为011,110,101,这三个结果发生的概率都相等,均为0.8×0.2,并且与哪两次中靶无关 因此,3次射击恰好2次中靶的概率为C经×0.82×0.2.同理可求中靶0次,1次,3次的概率 于是,中靶次数X的分布列为: P(X=k)=C×0.8×0.23-k,k=0,1,2,3 探究2:如果连续射击4次,类比上面的分析,表示中靶次数X等于2的结果有哪些?写出中靶次 数X的分布列. (1)表示中靶次数X等于2的结果有:A1A2A3A4,A1A2A3A4,A1A2A3A4,A1A2A3A4,A1 A2A3A4,A1A2A3A4,共6个。 (2)中靶次数X的分布列为:P(X=k)=C×0.8k×0.24-k,k=0,1,2,3,4 二项分布 一般地,在n重伯努利试验中,设每次试验中事件A发生的概率为p(O<p<I),用X表示事件 A发生的次数,则X的分布列为 P(X=k)=C晓×pk×(1-p)n-k,k=0,1,,n 如果随机变量X的分布列具有上式的形式,则称随机变量X服从二项分布(binomial distribution), 记作X~Bn,p) Cap"q"Cup'q Cp'q叶 Cpq° 事件A发生的概率 事件A发生的概率 P(X=k)=C pk(1-p)(其中k=0,1,2,…,m) 试验总次数 事件A发生的次数 思考1:二项分布与两点分布有何关系? 两点分布是一种特殊的二项分布,即是=1的二项分布:二项分布可以看做两点分布的一般形式 思考2:对比二项分布和二项式定理,你能看出他们之间的联系吗? 如果把p看成b,1-p看成a,则C×pk×(1-p)n-k就是二项式[(1-p)+p]m的展开式的通项,由 此才称为二项分布。 即∑k=oP(x=k)=∑k=oC×pk×(1-p)n-k=[p+(1-p)]m=l
为了简化表示,每次射击用 1 表示中靶,用 0 表示脱靶,那么 3 次射击恰好 2 次中靶的所有可能结 果可表示为 011,110,101,这三个结果发生的概率都相等,均为 0.8 2 ×0.2,并且与哪两次中靶无关. 因此,3 次射击恰好 2 次中靶的概率为 .同理可求中靶 0 次,1 次,3 次的概率. 于是,中靶次数 的分布列为: , , , 探究 2:如果连续射击 4 次,类比上面的分析,表示中靶次数 X 等于 2 的结果有哪些?写出中靶次 数 X 的分布列. (1)表示中靶次数 X 等于 2 的结果有: ̅ ̅ , ̅ ̅ ,, ̅ ̅ , ̅ ̅ ̅ ̅ , ̅ ̅ ,共 6 个。 (2)中靶次数 X 的分布列为: , , , 二项分布 一般地,在 n 重伯努利试验中,设每次试验中事件 A 发生的概率为 p(0<p<1),用 X 表示事件 A 发生的次数,则 X 的分布列为 , ,n. 如果随机变量 X 的分布列具有上式的形式,则称随机变量 X 服从二项分布(binomial distribution), 记作 X~B(n,p). X 0 1 … k … n p 0 0 n C p q n 1 1 1 n C p q n … k k n k C p q n … n n 0 C p q n 思考 1:二项分布与两点分布有何关系? 两点分布是一种特殊的二项分布,即是 n=1 的二项分布;二项分布可以看做两点分布的一般形式. 思考 2:对比二项分布和二项式定理,你能看出他们之间的联系吗? 如果把 p 看成 b,1-p 看成 a,则 就是二项式 的展开式的通项,由 此才称为二项分布。 即∑ ∑ =1

三、典例解析 例1:将一枚质地均匀的硬币重复抛掷10次,求: (1)恰好出现5次正面朝上的概率: (2)正面朝上出现的频率在0.4,0.6)内的概率 分析:抛掷一枚质地均匀的硬币,出现“正面朝上”和“反面朝上”两种结果且可能性相等,这是一个10重 伯努利试验,因此,正面朝上的次数服从二项分布。 解:设A=“正面朝上”,则P(A)=0.5.用X表示事件A发生的次数,X~B(10,0.5) (1)恰好出现5次正面朝上等价于X=5,于是 PX=5)=c品×050-器=器 (2)正面朝上出现的频率在[0.4,0.6]内等价于4sX≤6,于是 4≤X≤6)=C6×0.510+C×0.510+C×0.50=022=2 例2:如图是一块高尔顿板的示意图在一块木板上钉着若干排相互平行但相互错开的圆柱形小木钉, 小木钉之间留有适当的空隙作为通道,前面挡有一块玻璃,将小球从顶端放入,小球下落的过程中, 每次碰到小木钉后都等可能地向左或向右落下,最后落入底部的格子中格子从左到右分别编号为0, 1,2,,10,用X表示小球最后落入格子的号码,求X的分布列。 解:设A=“向右下落”,则A=“向左下落”,且P(A)=P(A=0.5.因为小球最后落入格子的号码X等于事 件A发生的次数,而小球在下落的过程中共碰撞小木钉10次,所以X~B(10,0.5).于是,X的分 布列为P(X=k)=C×0.510,k=0,1,,10. X的概率分布图如下图所示: 0.30 0.20 0.10 0.00 012345678910
三、典例解析 例 1 :将一枚质地均匀的硬币重复抛掷 10 次,求: (1)恰好出现 5 次正面朝上的概率; (2)正面朝上出现的频率在[0.4,0.6]内的概率. 分析:抛掷一枚质地均匀的硬币,出现“正面朝上”和“反面朝上”两种结果且可能性相等,这是一个 10 重 伯努利试验,因此,正面朝上的次数服从二项分布。 解:设 A=“正面朝上”,则 P(A)=0.5.用 X 表示事件 A 发生的次数,X~B(10,0.5). (1)恰好出现 5 次正面朝上等价于 X=5,于是 ; (2)正面朝上出现的频率在[0.4,0.6]内等价于 4≤ ≤6,于是 例 2:如图是一块高尔顿板的示意图.在一块木板上钉着若干排相互平行但相互错开的圆柱形小木钉, 小木钉之间留有适当的空隙作为通道,前面挡有一块玻璃,将小球从顶端放入,小球下落的过程中, 每次碰到小木钉后都等可能地向左或向右落下,最后落入底部的格子中.格子从左到右分别编号为 0, 1,2,…,10,用 X 表示小球最后落入格子的号码,求 X 的分布列。 解:设 A=“向右下落”,则 ̅=“向左下落”,且 P(A)=P( ̅)=0.5.因为小球最后落入格子的号码 X 等于事 件 A 发生的次数,而小球在下落的过程中共碰撞小木钉 10 次,所以 X~B(10,0.5).于是,X 的分 布列为 , ,10. X 的概率分布图如下图所示: 0.00 0.10 0.20 0.30 0 1 2 3 4 5 6 7 8 9 10

二项分布中需要注意的问题和关注点 (I)当X服从二项分布时,应弄清X~B(n,p)中的试验次数n与成功概率p. (2)解决二项分布问题的两个关注点 ①对于公式PX=k)=Cp1-p)-k=0,1,2,,n),必须在满足“独立重复试验时才能 应用,否则不能应用该公式. ②判断一个随机变量是否服从二项分布,关键有两点:一是对立性,即一次试验中,事件发生与否 两者必有其一:二是重复性,即试验是独立重复地进行了n次. 例3:甲、乙两选手进行象棋比赛,如果每局比赛甲获胜的概率为0.6,乙获胜的概率为0.4,那么 采用3局2胜制还是采用5局3胜制对甲更有利? 解法一:采用3局2胜制,甲最终获胜有两种可能的比分2:0或2:1,前者是前两局甲连胜,后 者是前两局甲、乙各胜一局且第3局甲胜因为每局比赛的结果是独立的,甲最终获胜的概率为 p1=0.62+C2×0.62×0.4=0.648. 类似地,采用5局3胜制,甲最终获胜有3种比分3:0,3:1或3:2因为每局比赛的结果是独立 的,所以甲最终获胜的概率为p2=0.63+C号×0.63×0.4+C¥×0.63×0.42=0.68256 解法2:采用3局2胜制,不妨设赛满3局,用X表示3局比赛中甲胜的局数,则X~B(3,0.6.甲 最终获胜的概率为p1=P(X=2+PX=3FC号×0.62×0.4+C3×0.63=0.648. 采用5局3胜制,不妨设赛满5局,用X表示5局比赛中甲胜的局数, 则XB(5,0.6) 甲最终获胜的概率为p2=P(X=3)+P(X=4)+P(X=5) =C×0.63×0.42+C4×0.64×0.4+C×0.65=0.68256 因为2>p1,所以5局3胜制对甲有利.实际上,比赛局数越多,对实力较强者越有利, 探究3:假设随机变量X服从二项分布B(nP),那么X的均值和方差是什么? (1)当n=1时,X服从两点分布,分布列为P(X=0)=1-p,P(X=1)= p.均值和方差分别为E(X凶=p;D(=p(1-p): (2)当n=2时,X的分布列为 P(X=0)=(1-p)2,P(X=1)=2p(1-p), PX=2)=p2.均值和方差分别为E(X)=0×(1-p)2+1×2p(1-p)+2×p2=2p.D(X) =02×(1-p)2+12×2p(1-p)+22×p2-(2p)2=2p(1-p). 一般地,如果X~B(n,p),那么EX)=np;D(X)=p(1-p以
二项分布中需要注意的问题和关注点 (1)当 X 服从二项分布时,应弄清 X~B(n,p)中的试验次数 n 与成功概率 p. (2)解决二项分布问题的两个关注点 ①对于公式 P(X=k)=C k n p k (1-p)n-k (k=0,1,2,…,n),必须在满足“独立重复试验”时才能 应用,否则不能应用该公式. ②判断一个随机变量是否服从二项分布,关键有两点:一是对立性,即一次试验中,事件发生与否 两者必有其一;二是重复性,即试验是独立重复地进行了 n 次. 例 3:甲、乙两选手进行象棋比赛,如果每局比赛甲获胜的概率为 0.6,乙获胜的概率为 0.4,那么 采用 3 局 2 胜制还是采用 5 局 3 胜制对甲更有利? 解法一:采用 3 局 2 胜制,甲最终获胜有两种可能的比分 2:0 或 2:1,前者是前两局甲连胜,后 者是前两局甲、乙各胜一局且第 3 局甲胜.因为每局比赛的结果是独立的,甲最终获胜的概率为 . 类似地,采用 5 局 3 胜制,甲最终获胜有 3 种比分 3:0,3:1 或 3:2 因为每局比赛的结果是独立 的,所以甲最终获胜的概率为 . 解法 2:采用 3 局 2 胜制,不妨设赛满 3 局,用 X 表示 3 局比赛中甲胜的局数,则 X~B(3,0.6).甲 最终获胜的概率为 =P(X=2)+P(X=3)= =0.648. 采用 5 局 3 胜制,不妨设赛满 5 局,用 X 表示 5 局比赛中甲胜的局数, 则 X~B(5,0.6). 甲最终获胜的概率为 + =0.68256 因为 ,所以 5 局 3 胜制对甲有利.实际上,比赛局数越多,对实力较强者越有利. 探究 3:假设随机变量 X 服从二项分布 B(n,p),那么 X 的均值和方差是什么? (1) 当 时, 服从两点分布,分布列为 均值和方差分别为 当 时, 的分布列为 均值和方差分别为 ( ) ( ) ( ) 一般地,如果 X~B(n,p),那么 E(X)=np; D(X)=np(1-p)

七、教学反思
七、教学反思