
全程设计 第七章 万有引力与宇宙航行 3 万有引力理论的成就
第七章 万有引力与宇宙航行 3 万有引力理论的成就
素养·目标定位 课前·基础认知 课堂·重难突破 模型方法·素养提升 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练 模型方法·素养提升

导 素养.目标定位 目标素养 1.通过计算天体的质量和发现未知天体,体会万有引力定律在 天文学上的重要性。 2.掌握计算天体质量和密度的方法。 3.通过计算天体的质量和密度,体会解决天体运动问题的基本 思路,掌握解决问题的科学思维和方法
导航 1.通过计算天体的质量和发现未知天体,体会万有引力定律在 天文学上的重要性。 2.掌握计算天体质量和密度的方法。 3.通过计算天体的质量和密度,体会解决天体运动问题的基本 思路,掌握解决问题的科学思维和方法。 素养·目标定位 目 标 素 养
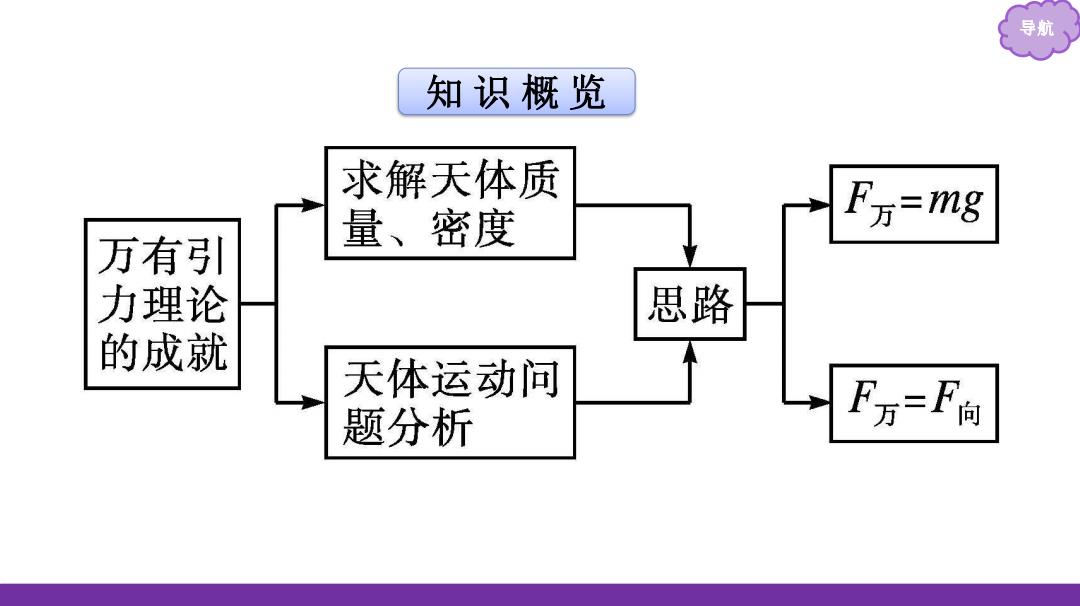
导航 知识概览 求解天体质 量、密度 -mg 万有引 力理论 思路 的成就 天体运动问 题分析 F万=F向
导航 知 识 概 览

导 课前·基础认知 一、“称量”地球的质量 1.依据:若不考虑地球自转的影响,地面上质量为m的物体所 受的重力等于地球对物体的引力,即 2.结论:m地= ,只要知道g、R的值,就可计算出地球的 质量
导航 一、“称量”地球的质量 1.依据:若不考虑地球自转的影响,地面上质量为 m 的物体所 受的重力等于地球对物体的引力,即 mg = G 𝒎地 𝒎 𝑹𝟐 。 2.结论:m 地= 𝒈𝑹 𝟐 𝑮 ,只要知道 g、R 的值,就可计算出地球的 质量。 课前·基础认知

导 微思考1969年7月20日,美国宇航员阿姆斯特朗在月球上留 下了人类第一只脚印,迈出了人类征服宇宙的一大步。若宇 航员在月球上用弹簧测力计测出质量为的物体的重力为F。 能否利用这个条件估测月球的质量?(已知月球半径为) 提示能。设月球质量为m则F-C”故m
导航 微思考1969年7月20日,美国宇航员阿姆斯特朗在月球上留 下了人类第一只脚印,迈出了人类征服宇宙的一大步。若宇 航员在月球上用弹簧测力计测出质量为m的物体的重力为F。 能否利用这个条件估测月球的质量?(已知月球半径为R) 提示:能。设月球质量为 m 月,则 F=G 𝒎月 𝒎 𝑹𝟐 ,故 m 月= 𝑭𝑹 𝟐 𝑮𝒎

导月 二、计算天体的质量 1.太阳质量的计算。 (1)依据:质量为m的行星绕太阳做匀速圆周运动时,行星与太 阳间的万有引力充当向心力,即G”太” r2 (2)结论:m太= ,只要知道行星绕太阳运动的公转周期 T和它与太阳的距离”,就可以计算出太阳的质量
导航 二、计算天体的质量 1.太阳质量的计算。 (1)依据:质量为 m 的行星绕太阳做匀速圆周运动时,行星与太 阳间的万有引力充当向心力,即 G𝒎太 𝒎 𝒓 𝟐 = 𝟒 𝛑 𝟐 𝒎 𝒓 𝑻 𝟐 。 (2)结论:m 太 = 𝟒 𝛑 𝟐 𝒓 𝟑 𝑮 𝑻 𝟐 ,只要知道行星绕太阳运动的公转周期 T 和它与太阳的距离 r,就可以计算出太阳的质量

导 2.其他行星质量的计算。 ()依据:绕行星做匀速圆周运动的卫星,同样满足Gm行m r2 (m行为行星质量,m为卫星质量)。 (2)结论:m行= ,只要知道卫星绕行星运动的周期T和轨 道半径r,就可以计算出行星的质量
导航 2.其他行星质量的计算。 (1)依据:绕行星做匀速圆周运动的卫星,同样满足 G 𝒎行 𝒎 𝒓 𝟐 = 𝟒𝛑 𝟐 𝒎𝒓 𝑻𝟐 (m 行为行星质量,m 为卫星质量)。 (2)结论:m 行= 𝟒𝛑 𝟐 𝒓 𝟑 𝑮𝑻𝟐 ,只要知道卫星绕行星运动的周期 T 和轨 道半径 r,就可以计算出行星的质量

导航 微训练1.仅已知地球绕太阳运行的公转轨道半径r,公转周期 T,引力常量G,可估算出() A地球的质量 B.太阳的质量 C地球的密度 D.太阳的密度 答案:B 解析:根据 mr可求出太阳的质量m 4π2 r2 G7,不知太 阳的半径,无法求太阳的密度,环绕天体地球的质量、密度无法 计算,选项B正确,A、C、D错误
导航 微训练1.仅已知地球绕太阳运行的公转轨道半径r,公转周期 T,引力常量G,可估算出( ) A.地球的质量 B.太阳的质量 C.地球的密度 D.太阳的密度 答案:B 解析:根据 G 𝒎太 𝒎 𝒓 𝟐 =m 𝟒𝛑 𝟐 𝑻𝟐 r 可求出太阳的质量 m 太= 𝟒𝛑 𝟐 𝑮𝑻𝟐 r 3 ,不知太 阳的半径,无法求太阳的密度,环绕天体地球的质量、密度无法 计算,选项 B 正确,A、C、D 错误

导航 2.右图是一行星绕恒星做匀速圆周运动的 示意图,由天文观测可得其运行周期为T,速 行星 度为y,引力常量为G,试求: 恒星 (1)行星运动的轨道半径R; (2)行星运动的加速度; (3)恒星的质量。 答案:(1(22℃
导航 2.右图是一行星绕恒星做匀速圆周运动的 示意图,由天文观测可得其运行周期为T,速 度为v,引力常量为G,试求: (1)行星运动的轨道半径R; (2)行星运动的加速度; (3)恒星的质量m0。 答案:(1)𝒗𝑻 𝟐𝛑 (2)𝟐𝛑𝒗 𝑻 (3)𝒗 𝟑 𝑻 𝟐𝛑𝑮