
全程设计 章末核心素养整合
章末核心素养整合

知识体系构建 专题归纳突破
知识体系构建 专题归纳突破
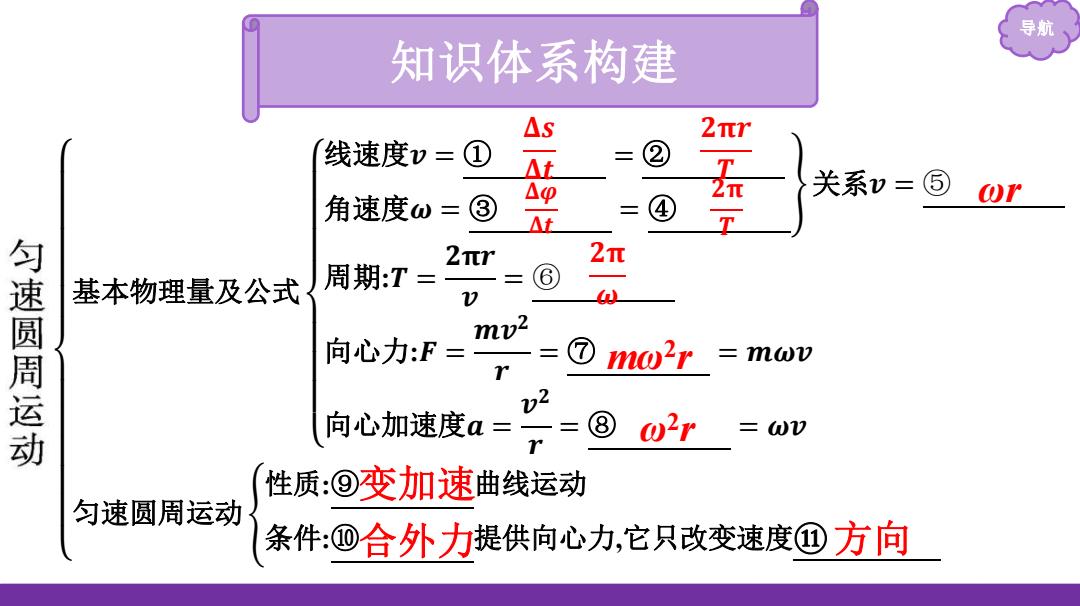
导航 知识体系构建 △S 2fr 线速度v = ① t △ 2π 关系v=⑤wr 角速度ω= ③ 三 △t 2πr 2π 匀速圆周运动 基本物理量及公式 周期:T= D mv2 向心力:F= ⑦ 三1 wv v2 向心加速度a= ⑧ 02r =ω) 性质:⑨变加速曲线运动 匀速圆周运动 条件:四合外力提供向心力,它只改变速度①方向
导航 基本物理量及公式 线速度𝒗 = ① = ② 角速度𝝎 = ③ = ④ 关系𝒗 = ⑤ 周期:𝑻 = 𝟐𝛑𝒓 𝒗 = ⑥ 向心力:𝑭 = 𝒎𝒗 𝟐 𝒓 = ⑦ = 𝒎𝝎𝒗 向心加速度𝒂 = 𝒗 𝟐 𝒓 = ⑧ = 𝝎𝒗 匀速圆周运动 性质:⑨ 曲线运动 条件:⑩ 提供向心力,它只改变速度⑪ 𝚫𝒔 𝚫𝒕 𝟐𝛑𝒓 𝑻 𝚫𝝋 𝚫𝒕 𝟐𝛑 𝑻 ωr 𝟐𝛑 𝝎 mω2 r ω2 r 变加速 合外力 方向 知识体系构建
导航 火车转弯的实例分析 匀速圆周运动 汽车过拱形桥:竖直平面内的圆周运动 圆周运动的实例分析 航天器中的失重现象 应用 离心运动 危害的防止
导航 圆周运动的实例分析 火车转弯的实例分析 汽车过拱形桥:竖直平面内的圆周运动 航天器中的失重现象 离心运动 应用 危害的防止

专题归纳突破 专题一圆周运动的动力学问题求解圆周运动的动力学问题 大致可以分为三步: 1.分析物体的运动情况,明确圆周运动的轨道平面,确定圆心 的位置和半径的大小,从而确定向心力的方向。 2.分析物体的受力情况,弄清向心力的来源。利用直接合成法 或正交分解法,求出沿半径方向的合力F,即为向心力。 3.由牛顿第二定律F=ma列方程求解相应问题,其中Fn是向心 力,是向心加速度,向心加速度往往用、or或把来表示
导航 专题一 圆周运动的动力学问题求解圆周运动的动力学问题 大致可以分为三步: 1.分析物体的运动情况,明确圆周运动的轨道平面,确定圆心 的位置和半径的大小,从而确定向心力的方向。 2.分析物体的受力情况,弄清向心力的来源。利用直接合成法 或正交分解法,求出沿半径方向的合力Fn ,即为向心力。 3.由牛顿第二定律Fn=ma列方程求解相应问题,其中Fn是向心 力,a是向心加速度,向心加速度a往往用 来表示。 𝒗 𝟐 𝒓 、ω2 r 或 r 𝟒𝛑 𝟐 𝑻𝟐 专题归纳突破
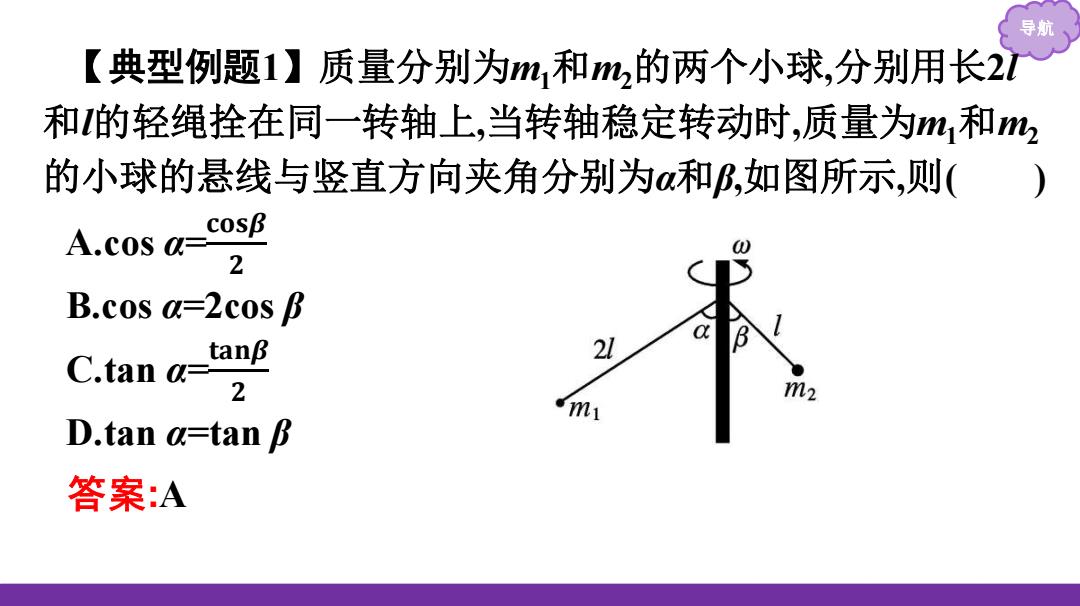
导为 【典型例题1】质量分别为m,和m的两个小球,分别用长2l 和的轻绳拴在同一转轴上,当转轴稳定转动时,质量为m和m2 的小球的悬线与竖直方向夹角分别为和β,如图所示,则( cosβ A.cos a- 2 B.cos a=2cos B C.tan a= tanβ 21 2 m2 D.tan a=tan B 答案:A
导航 【典型例题1】质量分别为m1和m2的两个小球,分别用长2l 和l的轻绳拴在同一转轴上,当转轴稳定转动时,质量为m1和m2 的小球的悬线与竖直方向夹角分别为α和β,如图所示,则( ) A.cos α= 𝐜𝐨𝐬𝜷 𝟐 B.cos α=2cos β C.tan α= 𝐭𝐚𝐧𝜷 𝟐 D.tan α=tan β 答案:A

解析:对于质量为m,的球,受重力和绳子拉力作用,由两个力 的合力提供向心力,如图所示。 设它们转动的角速度是w,由mgtan a=m12 Isin aω2, 可得c0sa82。同理可得c0sf总则c0saa 选项A正确。 m2 m18
导航 解析:对于质量为m1的球,受重力和绳子拉力作用,由两个力 的合力提供向心力,如图所示。 设它们转动的角速度是ω,由m1gtan α=m1·2lsin α·ω2 , 可得 cos α= 𝒈 𝟐𝒍𝝎𝟐 。同理可得 cos β= 𝒈 𝒍𝝎𝟐 ,则 cos α= 𝐜𝐨𝐬𝜷 𝟐 , 选项A正确

导 【跟踪训练1】如图所示,一个光滑的圆锥体固定在水平桌 面上,其轴线沿竖直方向,母线与轴线之间的夹角0=30°。一条 长为的绳(质量不计),一端固定在圆锥体的顶点O处,另一端 拴着一个质量为m的小物体(物体可看作质点),物体以速率y 绕圆锥体的轴线做水平匀速圆周运动。 (当= 时,求绳对物体的拉力。 2)当2时,求绳对物体的拉力。 2
导航 【跟踪训练1】如图所示,一个光滑的圆锥体固定在水平桌 面上,其轴线沿竖直方向,母线与轴线之间的夹角θ=30°。一条 长为l的绳(质量不计),一端固定在圆锥体的顶点O处,另一端 拴着一个质量为m的小物体(物体可看作质点),物体以速率v 绕圆锥体的轴线做水平匀速圆周运动。 (1)当 v1= 𝒈𝒍 𝟔 时,求绳对物体的拉力。 (2)当 v2= 𝟑𝒈𝒍 𝟐 时,求绳对物体的拉力

导航 答案:(1)1.03ng (2)2mg 解析:水平方向F1sin.Fc0s0=m5g① 竖直方向Frcos0+FNsin0=ng② 联立①②两式解得Fv=ngsin0- v2cos0 lsin0 由上式可看出当0、1、一定时,线速度越大,支持力F越 小,当v满足一定条件,设=y时,能使F、=0,此时锥面与物体间 恰好无相互作用,即
导航 答案:(1)1.03mg (2)2mg 解析:水平方向 FTsin θ-FNcos θ=m 𝒗 𝟐 𝒍𝐬𝐢𝐧𝜽 ① 竖直方向 FTcos θ+FNsin θ=mg② 联立①②两式解得 FN=mgsin θ-m 𝒗 𝟐 𝐜𝐨𝐬𝜽 𝒍𝐬𝐢𝐧𝜽 由上式可看出当θ、l、m一定时,线速度v越大,支持力FN越 小,当v满足一定条件,设v=v0时,能使FN =0,此时锥面与物体间 恰好无相互作用,即

导航 mgsin 0-m vo2cos0-O Isin0 得出w、 glsin20 cos0 将0=30°代入上式得y0= V3gl 6 ()当h91w时,物体在锥面上运动,联立①②两式解得 Fn-mgcos mm 2 mg+mg=1.03mg. 21
导航 mgsin θ-m 𝒗𝟎 𝟐 𝐜𝐨𝐬𝜽 𝒍𝐬𝐢𝐧𝜽 =0 得出 v0= 𝒈𝒍𝐬𝐢𝐧𝟐 𝜽 𝐜𝐨𝐬𝜽 将 θ=30°代入上式得 v0= 𝟑𝒈𝒍 𝟔 。 (1)当 v1= 𝟏 𝟔 𝒈𝒍<v0时,物体在锥面上运动,联立①②两式解得 FT1=mgcos θ+m𝒗𝟏 𝟐 𝒍 = 𝟑 𝟐 mg+𝟏 𝟔 mg=1.03mg