
全程设计 第七章 万有引力与宇宙航行 2 万有引力定律
第七章 万有引力与宇宙航行 2 万有引力定律
素养·目标定位 课前·基础认知 课堂·重难突破 模型方法·素养提升 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练 模型方法·素养提升

导奥 素养·目标定位 目标素养 1.学会通过行星运动规律的近似处理,从理论上探究向心力的 来源,结合开普勒第三定律演绎推导太阳与行星间的引力公 式。 2.通过行星运动规律结合月地检验理解万有引力定律的普遍 性。 3.掌握万有引力表达式的适用条件并能灵活应用。 4.知道引力常量测量的重要性
导航 1.学会通过行星运动规律的近似处理,从理论上探究向心力的 来源,结合开普勒第三定律演绎推导太阳与行星间的引力公 式。 2.通过行星运动规律结合月地检验理解万有引力定律的普遍 性。 3.掌握万有引力表达式的适用条件并能灵活应用。 4.知道引力常量测量的重要性。 素养·目标定位 目 标 素 养
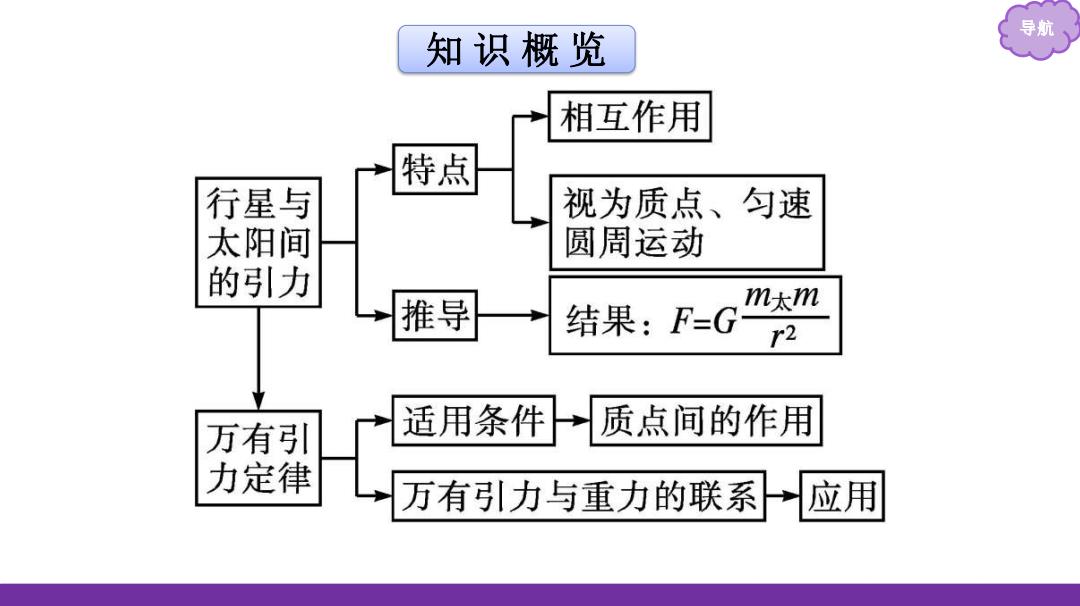
导航 知识概览 相互作用 特点 行星与 视为质点、匀速 太阳间 圆周运动 的引力 推导 m太m 结果:F=G r2 万有引 适用条件 质点间的作用 力定律 万有引力与重力的联系 应用
导航 知 识 概 览

导航 课前·基础认知 一、行星与太阳间的引力 1.模型简化。 行星以太阳为圆心做 运动,太阳对行星的引力 提供了行星做 运动的向心力
导航 一、行星与太阳间的引力 1.模型简化。 行星以太阳为圆心做 匀速圆周 运动,太阳对行星的引力 提供了行星做 匀速圆周 运动的向心力。 课前·基础认知

导 微思考如图所示,行星所做的匀速圆周运动与我们平常生活 中见到的匀速圆周运动是否符合同样的动力学规律?如果是, 分析行星的受力情况。 提示:行星与平常我们见到的做匀速圆周运动的物体一样, 遵守牛顿第二定律F=m,行星所需要的向心力由太阳对它 的引力提供
导航 微思考如图所示,行星所做的匀速圆周运动与我们平常生活 中见到的匀速圆周运动是否符合同样的动力学规律?如果是, 分析行星的受力情况。 提示:行星与平常我们见到的做匀速圆周运动的物体一样, 遵守牛顿第二定律F= ,行星所需要的向心力由太阳对它 的引力提供。 𝒎𝒗 𝟐 𝒓

导航 2.太阳对行星的引力。 Fmm)2= 4n2mr T2 结合开普勒第三定律得:F∝ 3.行星对太阳的引力。 根据牛顿第三定律,行星对太阳的引力F的大小也存在与上 述关系类似的结果,即F'∝
导航 2.太阳对行星的引力。 F=𝒎𝒗 𝟐 𝒓 =m 𝟐𝛑𝒓 𝑻 𝟐 · 𝟏 𝒓 = 𝟒𝛑 𝟐 𝒎𝒓 𝑻𝟐 。 结合开普勒第三定律得:F∝ 𝒎 𝒓 𝟐 。 3.行星对太阳的引力。 根据牛顿第三定律,行星对太阳的引力 F'的大小也存在与上 述关系类似的结果,即 F'∝ 𝒎太 𝒓 𝟐

导航 4.太阳与行星间的引力。 由于F、Fe李且F=则有F心 ,写成等式 F- ,式中G为比例系数
导航 4.太阳与行星间的引力。 由于 F∝ 𝒎 𝒓 𝟐 、F'∝ 𝒎太 𝒓 𝟐 ,且 F=F',则有 F∝ 𝒎太 𝒎 𝒓 𝟐 ,写成等式 F= G 𝒎太 𝒎 𝒓 𝟐 ,式中 G 为比例系数

二、月一地检验 假设地球与月球间的作用力和太阳与行星间的作用力是同一种 力,它们的表达式也应该满足F= 。根据牛顿第二定律, 月球绕地球做圆周运动的向心加速度α月= M月 假设地球对苹果的吸引力也是同一种力,同理可知,苹果的自由落 体加速度a华-G袋所以g m苹 。由于月球与地球中心的距 离r约为地球半径R的60倍,所以月- 0
导航 二、月 —地检验 假设地球与月球间的作用力和太阳与行星间的作用力是同一种 力,它们的表达式也应该满足 F= G𝒎 月 𝒎地 𝒓 𝟐 。根据牛顿第二定律, 月球绕地球做圆周运动的向心加速度 a 月 = 𝑭𝒎月 = G𝒎地𝒓𝟐 。 假设地球对苹果的吸引力也是同一种力,同理可知,苹果的自由落 体加速度 a 苹 = 𝑭𝒎苹 =G𝒎地𝑹𝟐 ,所以 𝒂 月 𝒂苹 = 𝑹 𝟐 𝒓 𝟐 。由于月球与地球中心的距 离 r 约为地球半径 R 的 60 倍,所以 𝒂 月 𝒂苹 = 𝟏𝟔𝟎 𝟐

微训练11.月一地检验的结果说明了() A.地面物体所受地球的引力与月球所受地球的引力是同一 种性质的力 B.地面物体所受地球的引力与月球所受地球的引力不是同 一种性质的力 C.地面物体所受地球的引力,只与物体的质量有关 D.月球所受地球的引力,只与月球的质量有关 答案:A
导航 微训练11.月—地检验的结果说明了( ) A.地面物体所受地球的引力与月球所受地球的引力是同一 种性质的力 B.地面物体所受地球的引力与月球所受地球的引力不是同 一种性质的力 C.地面物体所受地球的引力,只与物体的质量有关 D.月球所受地球的引力,只与月球的质量有关 答案:A