
中国绅学我术大学 University of Science and Technology of China 第5章 氧化-还原反应和电化学 Chapter 5 Oxidation-Reduction Reactions Electrochemistry
第 5 章 氧化-还原反应和电化学 Chapter 5 Oxidation-Reduction Reactions & Electrochemistry

>化学反应分类: √酸碱反应:广义酸碱理论 √氧化还原反应:有电子转移的反应 √自由基反应 ·电化学:用氧化还原反应来研究电源、电解和腐蚀的原理 >本章内容: √氧化还原反应方程式 √原电池,电池反应,电极反应 √电极电势概念及原电池的电动势 √Nernst方程-影响电极电势的因素 √电极电势的应用 2
化学反应分类: 酸碱反应:广义酸碱理论 氧化还原反应:有电子转移的反应 自由基反应 • 电化学:用氧化还原反应来研究电源、电解和腐蚀的原理 本章内容: 氧化还原反应方程式 原电池,电池反应,电极反应 电极电势概念及原电池的电动势 Nernst 方程-影响电极电势的因素 电极电势的应用 2

§5.1氧化-还原反应(Oxidation-Reduction Reactions) 一、氧化数(Oxidation Number)) 1.氧化数的概念 >定义:物质中元素所带(形式)电荷的数值 ·离子化合物中:氧化数等于正、负离子的电荷数 ·共价化合物中:氧化数为原子间共用电子对的偏移数 √非极性键共价分子(单质):元素的氧化数为零 √假设极性共价键中的电子都指定给电负性更大的原子 √极性键共价分子:氧化数为原子间共用电子对的偏移数 +1-1 +1-1-1+1 H:F H:O:H H0:0:H H0F (-2) (-1) (0) √平均(表观)氧化数:与单个原子实际氧化数的区别联系 0+6 L2+20S0 →2T+08t50S平均氧化数+52 S. SS平均氧化数+2 3 -2
一、氧化数 (Oxidation Number) 1. 氧化数的概念 定义:物质中元素所带(形式)电荷的数值 • 离子化合物中:氧化数等于正、负离子的电荷数 • 共价化合物中:氧化数为原子间共用电子对的偏移数 非极性键共价分子(单质):元素的氧化数为零 假设极性共价键中的电子都指定给电负性更大的原子 极性键共价分子:氧化数为原子间共用电子对的偏移数 平均(表观)氧化数:与单个原子实际氧化数的区别联系 I2 + 2 2I + 3 §5.1 氧化─还原反应(Oxidation-Reduction Reactions) 1 1 H :F 1 1 1 1 (-2) H:O:H 1 1 0 0 1 1 ( 1) H : O : O: H 1 1 +1 1 (0) H : :F O +6 2 S平均氧化数+2 S平均氧化数+5/2 +5 +5 0 0
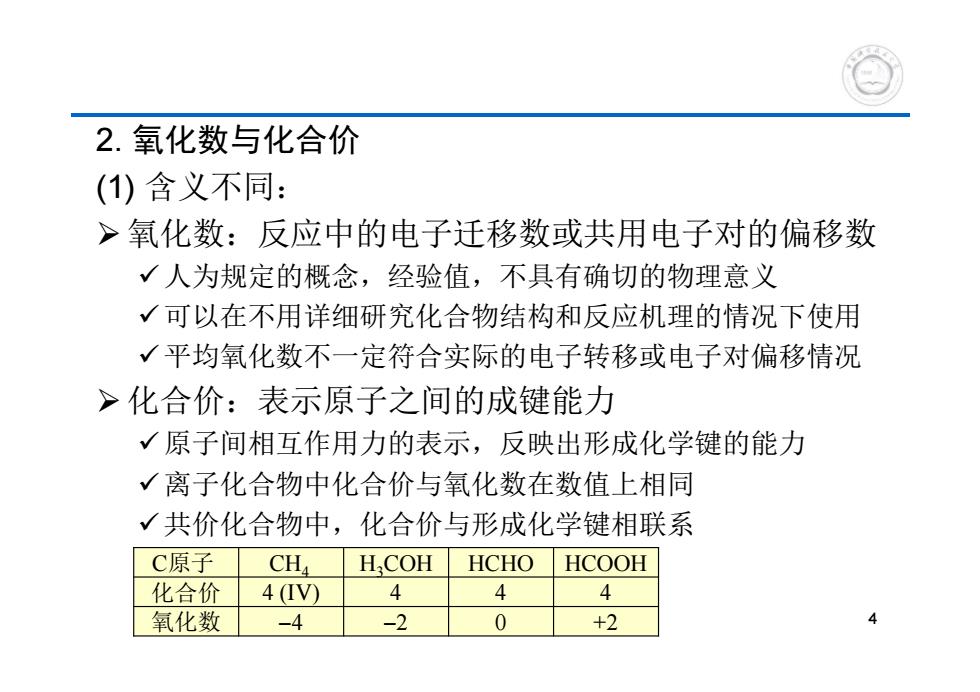
2.氧化数与化合价 (1)含义不同: >氧化数:反应中的电子迁移数或共用电子对的偏移数 √人为规定的概念,经验值,不具有确切的物理意义 √可以在不用详细研究化合物结构和反应机理的情况下使用 √平均氧化数不一定符合实际的电子转移或电子对偏移情况 >化合价:表示原子之间的成键能力 √原子间相互作用力的表示,反映出形成化学键的能力 √离子化合物中化合价与氧化数在数值上相同 √共价化合物中,化合价与形成化学键相联系 C原子 CH H.COH HCHO HCOOH 化合价 4(IV) 4 4 4 氧化数 -4 -2 0 +2 4
2. 氧化数与化合价 (1) 含义不同: 氧化数:反应中的电子迁移数或共用电子对的偏移数 人为规定的概念,经验值,不具有确切的物理意义 可以在不用详细研究化合物结构和反应机理的情况下使用 平均氧化数不一定符合实际的电子转移或电子对偏移情况 化合价:表示原子之间的成键能力 原子间相互作用力的表示,反映出形成化学键的能力 离子化合物中化合价与氧化数在数值上相同 共价化合物中,化合价与形成化学键相联系 4 C原子 CH4 H3COH HCHO HCOOH 化合价 4 (IV) 4 4 4 氧化数 4 2 0 +2

(2)取值范围不同: ·化合价取整数 ·氧化数可以取零、分数或整数 (3)符号/表示方法不同: ·氧化数:表示为+m、-n; 。 化合价: √离子化合物中,用m+、n-表示, √共价化合物中,用罗马字母表示,Fe(I)、Fe(II) 3.氧化数的应用 ·判断是否发生氧化还原反应配平氧化还原反应方程式 √氧化数升高←→还原剂←→发生氧化反应→生成氧化产物 √氧化数降低←→氧化剂←→发生还原反应→生成还原产物5
(2) 取值范围不同: • 化合价取整数 • 氧化数可以取零、分数或整数 (3) 符号/表示方法不同: • 氧化数:表示为 +m、n; • 化合价: 离子化合物中,用m+、n表示, 共价化合物中,用罗马字母表示,Fe (II)、Fe (III) 3. 氧化数的应用 • 判断是否发生氧化还原反应 配平氧化还原反应方程式 氧化数升高 还原剂 发生氧化反应 生成氧化产物 氧化数降低 氧化剂 发生还原反应 生成还原产物 5

4.氧化数确定的具体规定 (1)单质的氧化数为零:共用电子对不发生偏移 √例如P4、S中P、S的氧化数都为零 (2)氢的氧化数一般为+1, √但在NaH、CaH2、NaBH4、LiAIH4中氢的氧化数为-1 (3)氧的氧化数一般为-2,但有许多例外: √例如0,(-1/2)0(-1)0(-1/3)0(+1/2)0E,(+2) (4)所有氟化物中,氟的氧化数为-1 (5)配合物中: √中性分子为配体且提供偶数个电子,氧化数为零,如H,O、 CO、NH3、C2H4、C6H,等(例外:NO,亚硝酰基,+1) √自由基或原子团为配体时氧化数均看作-1,如-CH(-1)6
4. 氧化数确定的具体规定 (1) 单质的氧化数为零:共用电子对不发生偏移 例如P4、S8中P、S的氧化数都为零 (2) 氢的氧化数一般为+1, 但在NaH、CaH2、NaBH4、LiAlH4中氢的氧化数为1 (3) 氧的氧化数一般为2,但有许多例外: 例如 (4) 所有氟化物中,氟的氧化数为1 (5) 配合物中: 中性分子为配体且提供偶数个电子,氧化数为零,如H2O、 CO、NH3、C2H4、C6H6等(例外:NO, 亚硝酰基, +1 ) 自由基或原子团为配体时氧化数均看作1,如-CH3(1) 6 O ( 1/ 2) 2 2 O ( 1) 2 O ( 1/ 3) 3 2 O( ) 1/2 OF 2) 2 (

(6)各元素可能的氧化数与其在周期表中位置密切相关 ·元素基态原子的价电子排布 ·奇数族元素的奇氧化态稳定:例如CL,-1,+1,+3,+5,+7 ·偶数族元素的偶氧化态稳定:例如S,-2,+2,+4,+6 ·绝大多数元素的最高氧化态都等于其族数: √例如:Cr,最高氧化数+6,K2CI207,Cr05,Na2C2012, √Cr0s→CrO(O2)h,Na2Cr2012→Na[OCr(O2)5CrO]Na ·元素的最高氧化数为+8,例如OsO4,RuO4, (7)化合物中各原子的氧化数的代数和为零;复杂离子 的电荷等于各元素氧化数的代数和 ·例如:S,032-中0氧化数-2,推算出S平均氧化数+2 S4O62-中O氧化数-2,推算出S平均氧化数+5/2 7
(6) 各元素可能的氧化数与其在周期表中位置密切相关 • 元素基态原子的价电子排布 • 奇数族元素的奇氧化态稳定:例如 Cl, 1, +1, +3, +5, +7 • 偶数族元素的偶氧化态稳定:例如 S, 2, +2, +4, +6 • 绝大多数元素的最高氧化态都等于其族数: 例如:Cr,最高氧化数+6,K2Cr2O7,CrO5,Na2Cr2O12, CrO5 CrO(O2)2, Na2Cr2O12 Na[OCr(O2)5CrO]Na • 元素的最高氧化数为+8,例如 OsO4,RuO4, (7) 化合物中各原子的氧化数的代数和为零;复杂离子 的电荷等于各元素氧化数的代数和 • 例如:S2O32中O氧化数2,推算出S平均氧化数+2 S4O62中O氧化数2,推算出S平均氧化数+5/2 7

例1:下列各中心原子的氧化数(S、Mn、P)? (1)Na2S、H2S04、Na2S203、H2S、Na2S4O6S8 、K2S20g、H2S05、S4C2 (2)MnF2 MnO3F K4[Mn(CN)]KMnO Mn2(CO)10 Mn(CO)(NO) (3)HPO4P4O6、H3PO2、PH4、H3PO3y H2PO4、P4、H4P2O7、P2H4 8
例1:下列各中心原子的氧化数(S、Mn、P)? (1) Na2Sx、H2SO4、Na2S2O3、H2S、Na2S4O6、S8 、K2S2O8、H2SO5、S4Cl2 ( 2) MnF2、MnO3F、K4[Mn(CN)6]、K2MnO4、 Mn2(CO)10、Mn(CO)4(NO) (3) H3PO4、P4O6、H3PO2、PH4+、H3PO3、 H2PO4-、P4、H4P2O7、P2H4 8

二、氧化还原反应式配平(Balance of Redox Reactions) 1.氧化数法 >依据:氧化数的总升高值等于氧化数的总降低值 √还原剂失去电子总数=氧化剂得到电子的总数 >步骤:以P4+HC1O3HC1+HPO4为例 √正确书写反应物和生成物的分子式或离子式 √找出还原剂分子中所有原子的氧化数的总升高值和氧化剂 分子中所有原子的氧化数总降低值 4P:4×(+5-0)=+20,C1:-1-(+5)=-6 √找出两个数值的最小公倍数(60),进而求出氧化剂、还原剂 分子前面的系数(3,10) 3P4+10HC1O312H3PO4+10HC1 √由原子数守恒,补足不发生氧化还原变化的其他分子数 3P4+10HC103+18H20=12H3P04+10HC1 9
二、氧化还原反应式配平(Balance of Redox Reactions) 1. 氧化数法 依据:氧化数的总升高值等于氧化数的总降低值 还原剂失去电子总数 = 氧化剂得到电子的总数 步骤: 正确书写反应物和生成物的分子式或离子式 找出还原剂分子中所有原子的氧化数的总升高值和氧化剂 分子中所有原子的氧化数总降低值 找出两个数值的最小公倍数(60),进而求出氧化剂、还原剂 分子前面的系数(3,10) 由原子数守恒,补足不发生氧化还原变化的其他分子数 9

例:As2S3+HNO3→H3AsO4+H2SO4+NO 还原剂:2As:2×(5-3)=+4 283 3S:3×[6-(-2)】=+24 氧化剂:N:2-5=-3 x28 3As2S3+28HNO3->6H3AsO+9H2SO+28NO 补足后得:3As2S3+28HNO3+4H20一6H3AsO4+9H2SO4+28NO >例:P4+CuSO4+H20→Cu3P+H3PO4+H2SO4 氧化产物P(HP04):5-0=5 ×6 原产物P(CugP):-3-0=-3-6×5一 3Cu:3×(1-2)=-3 所以P的系数6+5=11,考虑P4,Cu,P和HPO4系数再乘4 即11P4+CuSO4+H20→(5×4)Cu3P+(6×4)HPO4+H2SO4 所以:11P4+60CuS04+96H20→20Cu3P+24H3P04+60H2S04
例:As2S3 + HNO3 H3AsO4 + H2SO4 + NO 还原剂: 氧化剂: 3As2S3 + 28HNO3 6H3AsO4 + 9H2SO4 + 28NO 补足后得: 例:P4 + CuSO4 + H2O Cu3P + H3PO4 + H2SO4 氧化产物 P (H3PO4) :5 0 = 5 还原产物 P (Cu3P) : 3 0 = 3 3Cu:3(1 2) = 3 所以P的系数 6 + 5 = 11,考虑P4,Cu3P和 H3PO4系数再乘4 即 11P4 + CuSO4 + H2O (54)Cu3P + (64)H3PO4 + H2SO4 所以:11P4 + CuSO4 + H2O 20Cu3P + 24H3PO4 + H2SO4 6 6 5 60 96 60