
4.数据的评价一显著性检验
4. 数据的评价——显著性检验

显著性检验的意义 利用统计学的方法,检验被处 理的问题是否存在统计上的 显著性差异
显著性检验的意义 • 利用统计学的方法,检验被处 理的问题 是否存在 统计上的 显著性差异

显著性检验的作用 分析工作者常常用标准方法与自已所用的分析 方法进行对照试验,然后用统计学方法检验两 种结果是否存在显著性差异。若存在显著性差 异而又肯定测定过程中没有错误,可以认定自 己所用的方法有不完善之处,即存在较大的系 统误差。 因此分析结果的差异需进行统计检验或显著性 ●
显著性检验的作用 • 分析工作者常常用标准方法与自己所用的分析 方法进行对照试验,然后用统计学方法检验两 种结果是否存在显著性差异。若存在显著性差 异而又肯定测定过程中没有错误,可以认定自 己所用的方法有不完善之处,即存在较大的系 统误差。 • 因此分析结果的差异需进行统计检验或显著性 检验

显著性检验的判断 对标准试样或纯物质进行测定,所得到的 平均值与标准值不完全一致; 2。 采用两种不同分析方法或不同分析人员对 同一试样进行分析时,所得两组数据的平 均值有一定的差异; 问题:差异是由什么原因引起的?偶然误差还是系统 误差?这类向题在统计学中属于“假设检验” 。 一如果分析结果之间存在“显著性差异”,就可认为 它们之间有明显的系统误差, 一否则就可以认为没有系统误差,仅为偶然误差引起 的正常情况
显著性检验的判断 1. 对标准试样或纯物质进行测定,所得到的 平均值与标准值不完全一致; 2. 采用两种不同分析方法或不同分析人员对 同一试样进行分析时,所得两组数据的平 均值有一定的差异; 问题:差异是由什么原因引起的 ? 偶然误差还是系统 误差 ?这类向题在统计学中属于“假设检验” 。 -如果分析结果之间存在“显著性差异” ,就可认为 它们之间有明显的系统误差, -否则就可以认为没有系统误差,仅为偶然误差引起 的正常情况

显著性检验的步骤 显著性检验的一般步骤是: 1.做一个假设,即假设不存在显著性差异,或所 有样本来源于同一体。 2.确定一个显著性水准,通常等于0.1,0.05,0.01 等值,分析工作中则多取0.05的显著性水准, 即置信度为95%。 3. 统计量计算和作出判断。 下面介绍t检验法和F检验法
显著性检验的步骤 显著性检验的一般步骤是: 1. 做一个假设,即假设不存在显著性差异,或所 有样本来源于同一体。 2. 确定一个显著性水准,通常等于0.1,0.05,0.01 等值,分析工作中则多取0.05的显著性水准, 即置信度为95%。 3. 统计量计算和作出判断。 • 下面介绍 t 检验法和 F检验法

t检验法 )平均值与标准值()的比较 a。计算t值 X -u 计算 b. 根据要求的置信度和测定次数查表,得:t表值 C. 比较: t针和t表 若针>t表,表示有显著性差异,存在系统误差, 被检验方法需要改进。 若t针《t,表示无显著性差异, 被检验方法可 以采用
t 检 验 法 b. 根据要求的置信度和测定次数查表,得:t表值 c. 比较: t计和t表 • 若t计 > t表,表示有显著性差异,存在系统误差, 被检验方法需要改进。 • 若t计 < t表,表示无显著性差异,被检验方法可 以采用。 n S X t 计算 a. 计算t 值 (1)平均值与标准值()的比较
例 采用某种新方法测定基准明矾中铝的质 量分数,得到下列9个分析数据10.74%, 10.77%,10.77%,10.77%,10.81%, 10.82%,10.73%,10.86%,10.81%。 己知明矾中铝含量的标准值(以理论值 代)为10.77%。试问采用该新方法后, 是否引起系统误差(置信度为5%)?
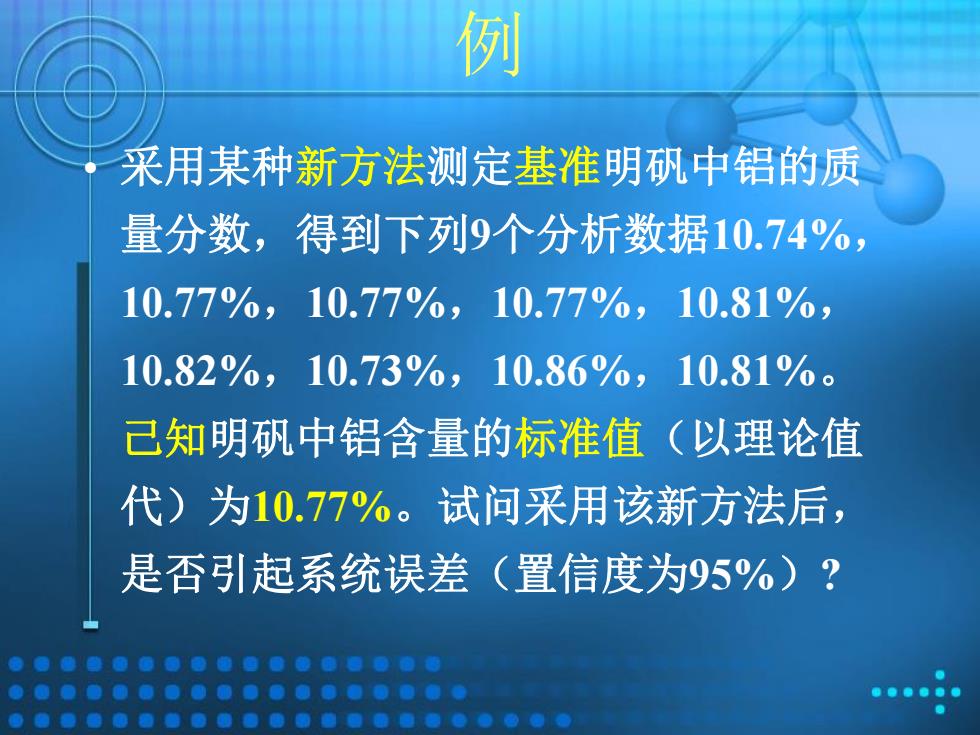
例 • 采用某种新方法测定基准明矾中铝的质 量分数,得到下列9个分析数据10.74%, 10.77%,10.77%,10.77%,10.81%, 10.82%,10.73%,10.86%,10.81%。 己知明矾中铝含量的标准值(以理论值 代)为10.77%。试问采用该新方法后, 是否引起系统误差(置信度为95%)?

解题过程 已知:n=9, f=9-1=8 求,平均值,标准偏差及值 X=10.79,S =0.042% x-u 10.79%-10.77% 9=1.43 S 0.042% t值表:当P=0.95,f=8时,t0.05,82.31 结论:tt(1.43)≤t表(2.31) 所以X与μ之间不存在显著性差异 即采用新方法没有起系统误差。 00000000000000000
解题过程 • 已知 : n=9, f =9-1=8 • 求:平均值,标准偏差及 t 值 9 1 .43 0 .042 % 10 .79 % 10 .77 % 10 .79 0 .042 % _ n S x t X ,S t 值表:当P=0.95,f =8 时,t0.05,8=2.31 结论:t计(1.43)<t表(2.31) 所以 与μ之间不存在显著性差异 即采用新方法没有引起系统误差。 X

(2)两组数据的平均值比较(同一试样) 两个分析人员测定的两组数据或采用不同的方 法测得的两组数据,经常出现差别。若要判断 这两个平均值之间是否有显著性差异,也采用 t检验法。设两组数据分别为: n S1 X n2 S2 (n一测定次数,s一标准偏差,1或2为组别) 先求合并的标准偏差$金和合并的t值 00
(2)两组数据的平均值比较(同一试样) • 两个分析人员测定的两组数据或采用不同的方 法测得的两组数据,经常出现差别。若要判断 这两个平均值之间是否有显著性差异,也采用 t检验法。设两组数据分别为: (n-测定次数,s-标准偏差,1或2为组别) • 先求合并的标准偏差S合和合并的t值 X1 X 2 n1 s1 n2 s2

S合与t合 差平方和 ∑(X-X)2+∑(X2,-X2)2 S合 总自由度 (n-1)+(n2-1) S合 或 (n1-1)S2+(n2-1)S n1+n2-2 再计算 IX-X2 t合= n n2 S n+n2 0000.0000 ●●●●● 0000●0000
S合与t合 总自由度 偏差平方和 s合 ( 1) ( 1) ( ) ( ) 1 2 2 2 2 2 1 1 n n X i X X i X = 2 ( 1) ( 1) 1 2 2 2 2 2 1 1 n n n S n S 或 S 合 1 2 1 2 1 2 | | n n n n S X X t 合 再计算 合