
第二章 误差与分析数据处理 ·21定量分析中的误差 22分析结果的数据处理 。 。23误差的传递(不要求 ·24有效数字及其运算规则 ·2.5标准曲线的回规分析不要求)
1 第二章 误差与分析数据处理 • 2.1 定量分析中的误差 • 2.2 分析结果的数据处理 • 2.3 误差的传递(不要求) • 2.4 有效数字及其运算规则 • 2.5 标准曲线的回规分析(不要求)

2.1定量分析中的误差 ☒无法品示该 2.1.1误差(Error)和准确度(accuracy) 误差:测定值(用x表示)与真值(true value,用T 表示)之差。 准确度:测定平均值与“真值”接近的程度,用 相对误差表示准确度. 绝对误差 E=X-T 相对误差 B= E×100% 2
2 2.1定量分析中的误差 2.1.1 误差(Error)和准确度(accuracy) 误差 :测定值(用x表示)与真值(true value,用T 表示)之差。 准确度: 测定平均值与“真值”接近的程度,用 相对误差表示准确度. 相对误差 绝对误差 Ea = x -T a r 100% E E T =
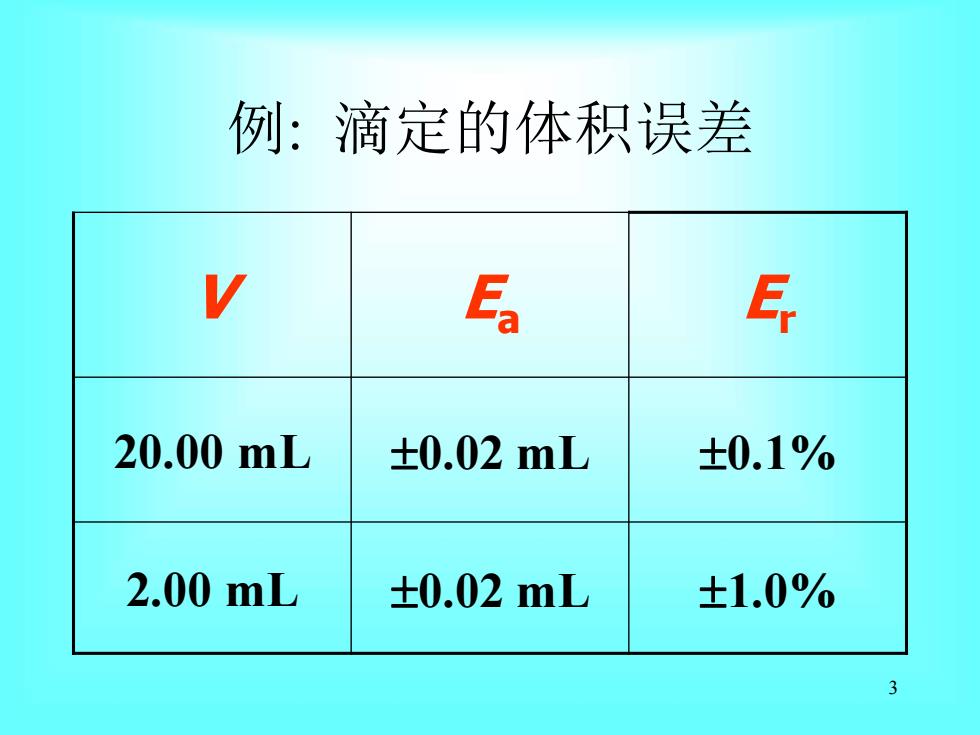
例:滴定的体积误差 E 20.00mL ±0.02mL ±0.1% 2.00mL ±0.02mL ±1.0% 3
3 例: 滴定的体积误差 V Ea Er 20.00 mL 0.02 mL 0.1% 2.00 mL 0.02 mL 1.0%

例:测定含铁样品中wFe),比较结果的准确度 A.铁矿中,T=62.38%,x=62.32% Ea=x-T=-0.06% B.Li2C03试样中,T=0.042%,x=0.044% Ea=x-T=0.002% A.E,= ×100%=-0.06/62.38=-0.1% 入 B.Er= ×100%=0.002/0.042=5%
4 例:测定含铁样品中w(Fe), 比较结果的准确度 A.铁矿中, T=62.38%, = 62.32% x Ea = x -T= -0.06% B. Li2CO3试样中, T=0.042%, =0.044% x Ea = x -T=0.002% a r A. 100% E E T = =-0.06/62.38=-0.1% a r B. 100% E E T = =0.002/0.042=5%

2.1.2偏差与精密度 ·偏差即各次测定值与平均值之差 ·精密度即平行测定的结果互相靠近的程 度 5
5 2.1.2偏差与精密度 • 偏差即各次测定值与平均值之差 • 精密度即平行测定的结果互相靠近的程 度

数据分散程度的表示 1.极差(全距R=xmax-xmin 相对极差RR(R/x)×100% 2.偏差 绝对偏差d=x:x 相对偏差Rd=(4/x)×100% 平均偏差: d=∑ldl/n d 相对平均偏差:Rd=二×100% C 6
6 数据分散程度的表示 1.极差(全距) R= xmax-xmin i 平均偏差: d = d n/ Rd 100% d x 相对平均偏差: = 相对极差 RR (R / x ) ×100% 2.偏差 绝对偏差 di = xi - x 相对偏差 Rdi = (di / x ) ×100%
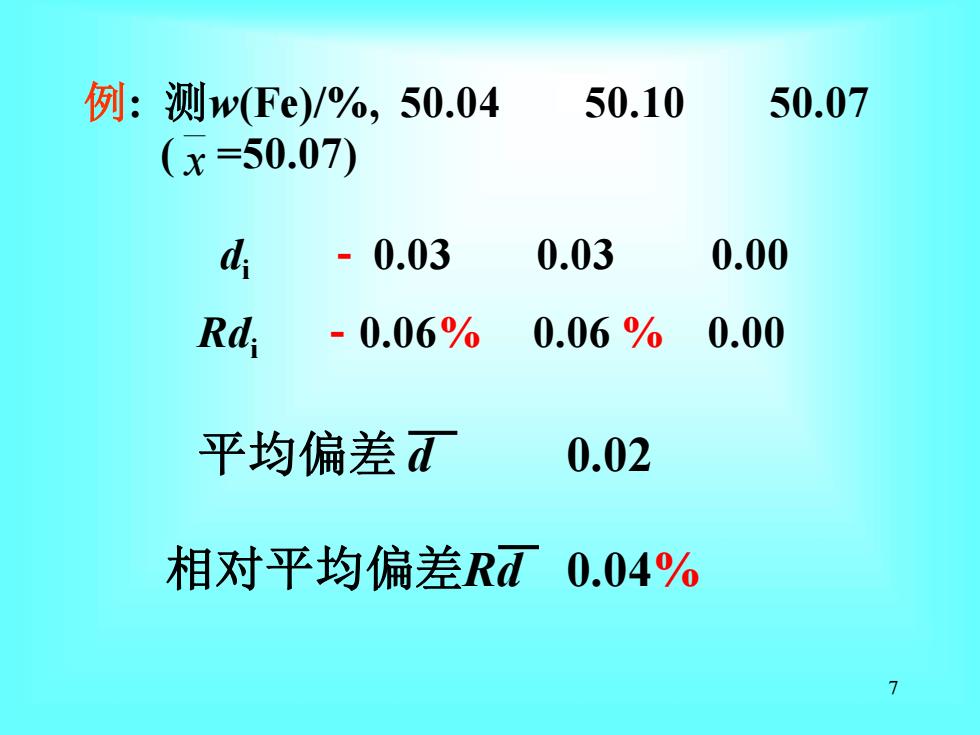
例:测w(Fe)/%,50.04 50.10 50.07 (x=50.07) d -0.03 0.03 0.00 Rd -0.06% 0.06% 0.00 平均偏差工 0.02 相对平均偏差Rd0.04% 7
7 例: 测w(Fe)/%, 50.04 50.10 50.07 ( =50.07) di -0.03 0.03 0.00 Rdi -0.06% 0.06 % 0.00 x 相对平均偏差Rd 0.04% 平均偏差 d 0.02

数据的集中趋势 1.平均值 Xi n i=1 例:测得c(NaOH)为 0.1012,0.1016,0.1014,0.1025(moL-) x=0.1017
8 数据的集中趋势 1 1 n i i x x n = = 1. 平均值 例:测得c(NaOH)为 0.1012, 0.1016, 0.1014, 0.1025 (mol·L-1 ) x = 0.1017

2.标准差 ∑s- 样本标准偏差:S=V n-1 (n-1)为自由度,用f表示 相对标准差(变异系数) CV=(s/x)X100%, 9
9 2. 标准差 2 i ( ) ? 1 x x n s − = − 样本标准偏差: ( -1) n f 为自由度,用 表示 相对标准差 (变异系数) CV=(s / ) x ×100%
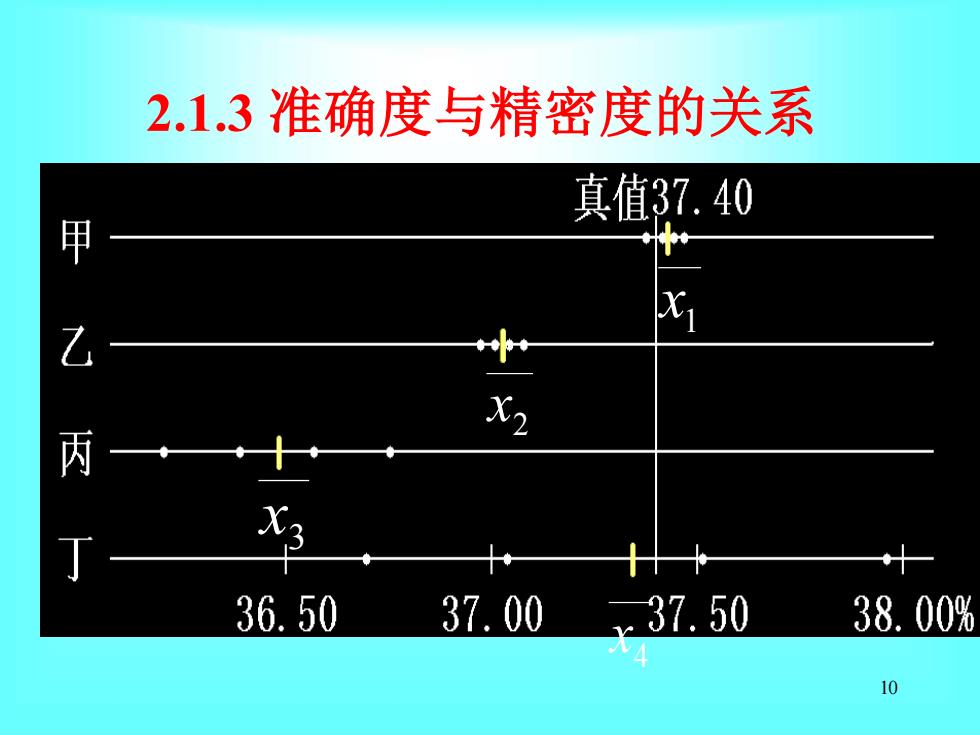
2.1.3准确度与精密度的关系 真值37.40 丙 36.50 37.00 37.50 38.00% 10
10 1 x 2 x 3 x 4 x 2.1.3 准确度与精密度的关系