
2-3工作曲线与回归分析
2-3 工作曲线与回归分析

工作曲线与回归分析的意义 在仪器分析法中,常利用被测组分的浓度 (或含量)和与其有定量关系的某一可测 的物理量间的线性关系来测定组分的含量。 但由于测量仪器本身的精密度及测量条件 较好的方法是:用数理统计的方法对数 据进行回归分析。 相关关系? ●●●
工作曲线与回归分析的意义 • 在仪器分析法中,常利用被测组分的浓度 (或含量)和与其有定量关系的某一可测 的物理量间的线性关系来测定组分的含量。 • 但由于测量仪器本身的精密度及测量条件 的细微波动,即使同一浓度的溶液,两次 测量结果也不会完全一致。因此,以测得 数据绘制的曲线时,往往会发生偏离。 • 如何才能得到数据点误差最小的直线和如 何估计直线上各点的精密度以及数据间的 相关关系? 较好的方法是:用数理统计的方法对数 据进行回归分析

例:吸光度法测定微量铁 测定步骤: 在一定条件下,以邻菲罗啉为显色剂, 配制铁标准液的浓度系列溶液,并测定 各浓度溶液的吸光度,得到浓度(C)与 对应吸光度(A)一系数据。以浓度为横 座标,以吸光度为纵坐标作图可得一曲 线称为标准曲线。在同一条件下对试样 进行测定,得到的A值后,可直接在曲线 上查出对应的C值。见下图
例:吸光度法测定微量铁 • 测定步骤: • 在一定条件下,以邻菲罗啉为显色剂, 配制铁标准液的浓度系列溶液,并测定 各浓度溶液的吸光度,得到浓度(C)与 对应吸光度(A)一系数据。以浓度为横 座标,以吸光度为纵坐标作图可得一曲 线称为标准曲线。在同一条件下对试样 进行测定,得到的A值后,可直接在曲线 上查出对应的C值。见下图
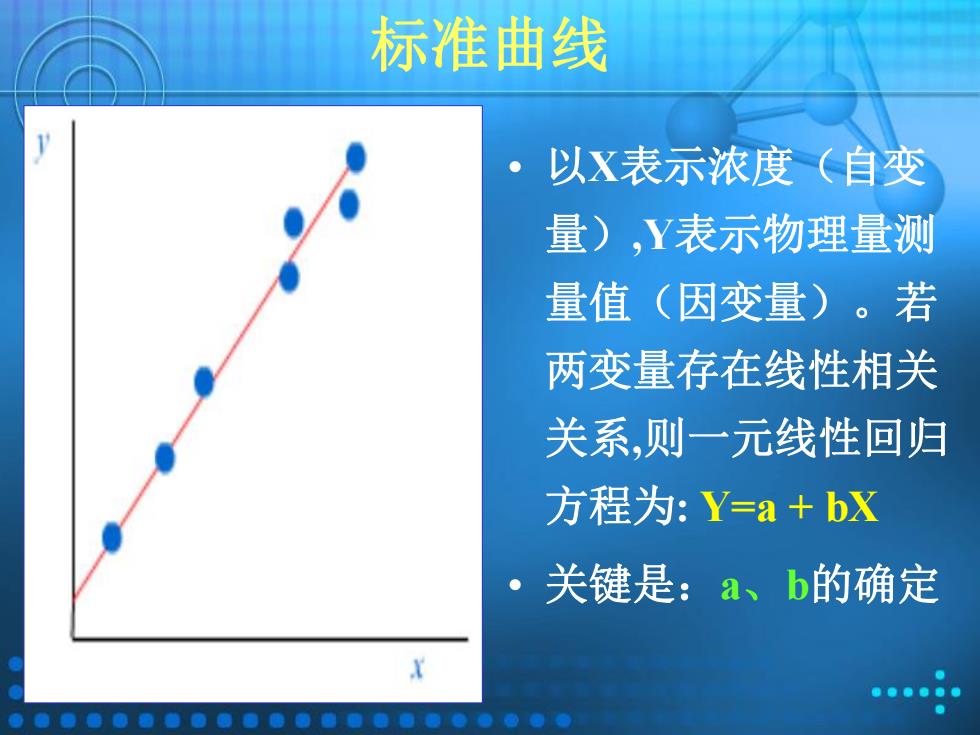
标准曲线 1 ● 以X表示浓度(自变 量),Y表示物理量测 量值(因变量)。若 两变量存在线性相关 关系,则一元线性回归 方程为:Y=a+bX 。 关键是:a、b的确定
标准曲线 • 以X表示浓度(自变 量),Y表示物理量测 量值(因变量)。若 两变量存在线性相关 关系,则一元线性回归 方程为: Y=a + bX • 关键是:a、b的确定

1、一元线性回归方程 在分析工作中,测量点X,Y)的波动主要来自 测量值的偏差。由于各人用肉眼观察连成的直 线不同,而影响分析结果的准确度。因此,可 用最小二乘法求出直线方程(回归线)。回归 线是X、Y线性关系的最佳曲线。a、b称回归 系数。依最小二乘法,用求极值的方法,可求 得如下公式: 00●0000
1、 一元线性回归方程 • 在分析工作中,测量点(Xi , Yi)的波动主要来自 测量值的偏差。由于各人用肉眼观察连成的直 线不同,而影响分析结果的准确度。因此,可 用最小二乘法求出直线方程(回归线)。回归 线是X、Y线性关系的最佳曲线。a、b称回归 系数。依最小二乘法,用求极值的方法,可求 得如下公式:

回归方程参数的计算 a,b称回归系数 ΣXY-∑XY) b ∑X-(X》 或b= Σ(X:-X)(Y:-Y ∑(X,-X)月 a Y-b Xi X= ∑X Y- ΣY n n
回归方程参数的计算 X X X Y X Y i n n b 2 2 i i i i i 2 i i i ( X X ) ( X X )( Y Y ) 或 b n X X i _ n Y Y i i _ _ a Y b X a, b 称回归系数

最佳的工作曲线 所以最佳的工作曲线是: (1)通过座标为(文,了)的点 (2)曲线的截距为a, 斜率为b 这样,在作图时就有严格的准则,同时 注明曲线的具体回归方程式。在未知物 的测定中也采用此方程式,由测得的响 应值Y来求得X未知
最佳的工作曲线 • 所以最佳的工作曲线是: • (1)通过座标为( , )的点 • (2)曲线的截距为 a,斜率为 b _X _Y • 这样,在作图时就有严格的准则,同时 注明曲线的具体回归方程式。在未知物 的测定中也采用此方程式,由测得的响 应值Y来求得X未知

例 用分光光度法测定SO,的含量时, 得到有关的数据如下: X SiO2 0 0.02 0.04 0.06 0.08 0.10 0.12 (mg) 吸光 0.032 0.135 0.187 0.268 0.359 0.435 0.511 度 试求校正曲线的回归方程,并求吸光 度为0.242的被测物含量。 0
例 • 试求校正曲线的回归方程,并求吸光 度为0.242的被测物含量。 用分光光度法测定SiO2的含量时, 得到有关的数据如下: X SiO2 (mg) 0 0.02 0.04 0.06 0.08 0.10 0.12 Y 吸光 度 0.032 0.135 0.187 0.268 0.359 0.435 0.511
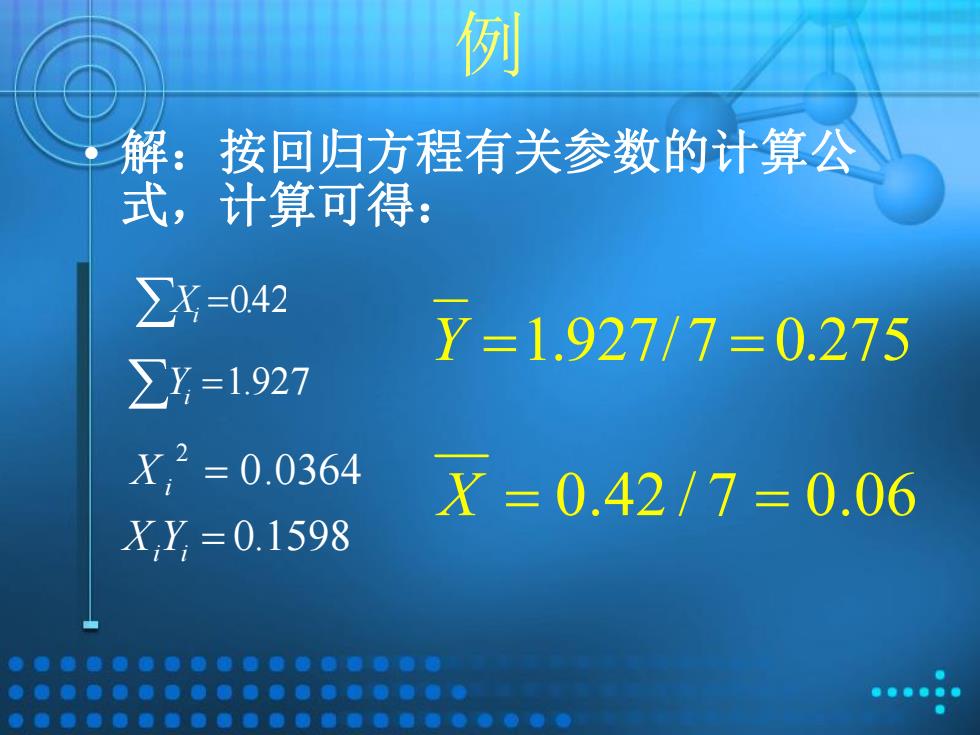
例 解:按回归方程有关参数的计算公 式,计算可得: ∑X=042 Y=1.927/7=0.275 ∑y=1.927 X2=0.0364 X=0.42/7=0.06 X,Y,=0.1598
例 • 解:按回归方程有关参数的计算公 式,计算可得: Xi 0.42 Yi 1.927 0.0364 2 Xi XiYi 0.1598 X 0.42 / 7 0.06 Y 1.927/ 7 0.275

解题 解:按回归方程有关参数的计算公式,计算可得: ∑X=042 n∑X,Y-∑X∑Y) b= ∑y=1.927 n∑X-(ΣX) X,2=0.0364 7×0.1597-(0.42)1.927 =3.94 7×0.0364-(0.42)2 X,Y=0.1598 a=Y-bX=0.275-3.94×0.06=0.039 校正曲线的回归方程:Y=0.039+3.94X 0000 00000
解 题 0.275 3.94 0.06 0.039 3.94 7 0.0364 (0.42) 7 0.1597 (0.42)(1.927) 2 2 2 a Y bX i n n b X X X Y X Y i i i i i 解:按回归方程有关参数的计算公式,计算 可得: Xi 0.42 Yi 1.927 0.0364 2 Xi XiYi 0.1598 校正曲线的回归方程∶ Y=0.039+3.94X