
3.少量次测量数据的统计处理 分析测试工作中,通过样本研究总体, 由于测量次数有限,c和无从知道,如 何处理和评价少量次数测定结果的数据? 而对多次测定的结果平均值又如何评价? 在前面己讨论的基础上,讨论下面的问 题: 0
3. 少量次测量数据的统计处理 • 分析测试工作中,通过样本研究总体, 由于测量次数有限, σ和μ无从知道,如 何处理和评价少量次数测定结果的数据? 而对多次测定的结果平均值又如何评价? 在前面己讨论的基础上,讨论下面的问 题:

几个基本概念 (1) 统计量值 (2)t分布曲线 (3)平均值的标准偏差 (4)平均值标准偏差与测量次数的关系 (5)平均值的置信区间 (6) 置信度与置信水平
几个基本概念 • (1)统计量t值 • (2)t 分布曲线 • (3)平均值的标准偏差 • (4)平均值标准偏差与测量次数的关系 • (5)平均值的置信区间 • (6)置信度与置信水平

(1)统计量t 分析化学中通过样本研究总体,由于测量次 数有限,ō和无从知道。英国统计学与化 学家Gosset提出用t分布解决了这一问题。使 不致因为用s代替σ而引起对正态分布的偏 离。 (1)分布和t分布曲线,统计量t,定义为: X S
(1)统计量t • 分析化学中通过样本研究总体,由于测量次 数有限, σ和μ无从知道。英国统计学与化 学家Gosset提出用t分布解决了这一问题。使 不致因为用 s 代替σ而引起对正态分布的偏 离。 • (1) t分布和t分布曲线,统计量t,定义为: s x x t
(2)t分布曲线f1,5,0 If(t) 英国的统计学兼化 0.4 学家Gosset)用笔名 =00 “Student'”发表论 文提出分布,故 得名。 0.2 分布曲线展示: -0.1 T分布曲线随自由 度f变化: 012 345 b. 当f=o时,t分布 t值 t分布曲线(f=1,5,∞) 则为正态分布
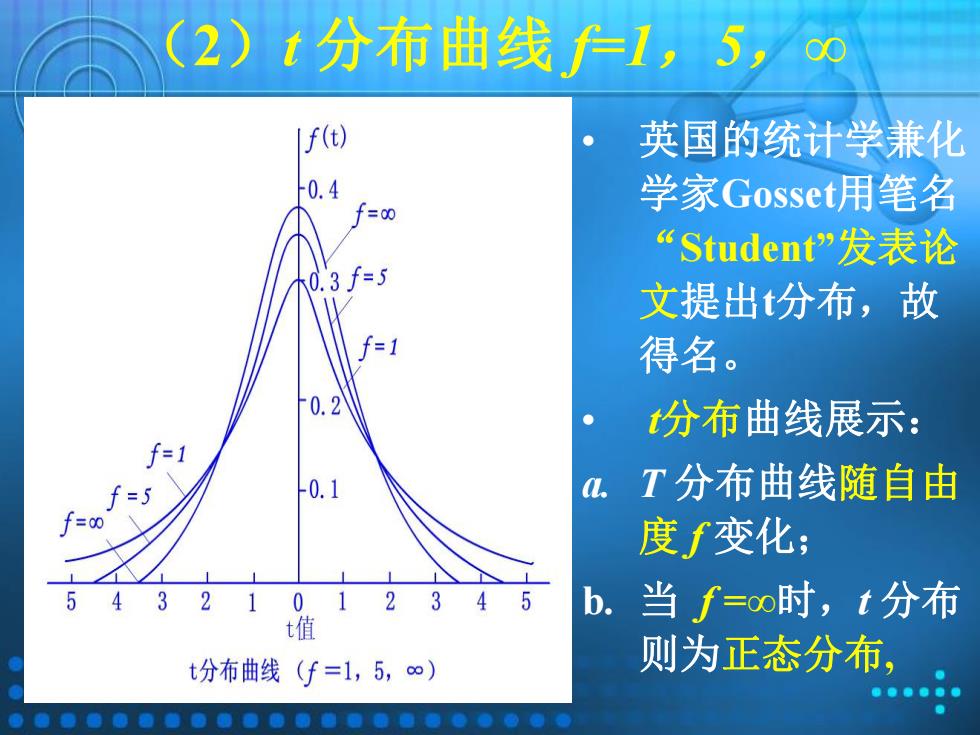
(2)t 分布曲线 f=1,5,∞ • 英国的统计学兼化 学家Gosset用笔名 “Student”发表论 文提出t分布,故 得名。 • t分布曲线展示: a. T 分布曲线随自由 度 f 变化; b. 当 f =∞时,t 分布 则为正态分布

t分布曲线 C. t分布曲线与横坐标t某区间所夹面积, 与正态分布曲线一样,表示测量值落在 该区间的概率。显然,若选定某一概率 和一定的自由度f,则t值也就一定。 d.由于t值与置信度及自由度有关,故其 表示为:ta,f
t 分布曲线 c. t 分布曲线与横坐标 t 某区间所夹面积, 与正态分布曲线一样,表示测量值落在 该区间的概率。显然,若选定某一概率 和一定的自由度f,则 t 值也就一定。 d. 由于t 值与置信度及自由度有关,故其 表示为:tα,f
t值表(双边) 置信度P,显著性水准C 置信度P,显著性水准a P=0.95 P=0.90 P=0.95 P=0.99 P=0.90 P=0.99 f=n-1 f=n-1 =0.05 0=0.10 0=0.05 0=0.01 0=0.10 a=0.01 6.31 12.71 63.66 7 1.90 2.36 3.50 2 2.92 4.30 9.92 8 1.86 2.31 3.36 3 2.35 3.18 5.84 9 1.83 2.26 3.25 4 2.13 2.78 4.60 10 1.81 2.23 3.17 5 2.02 2.57 4.03 20 1.72 2.09 2.84 6 1.94 2.45 3.71 00 1.64 1.96 2.58
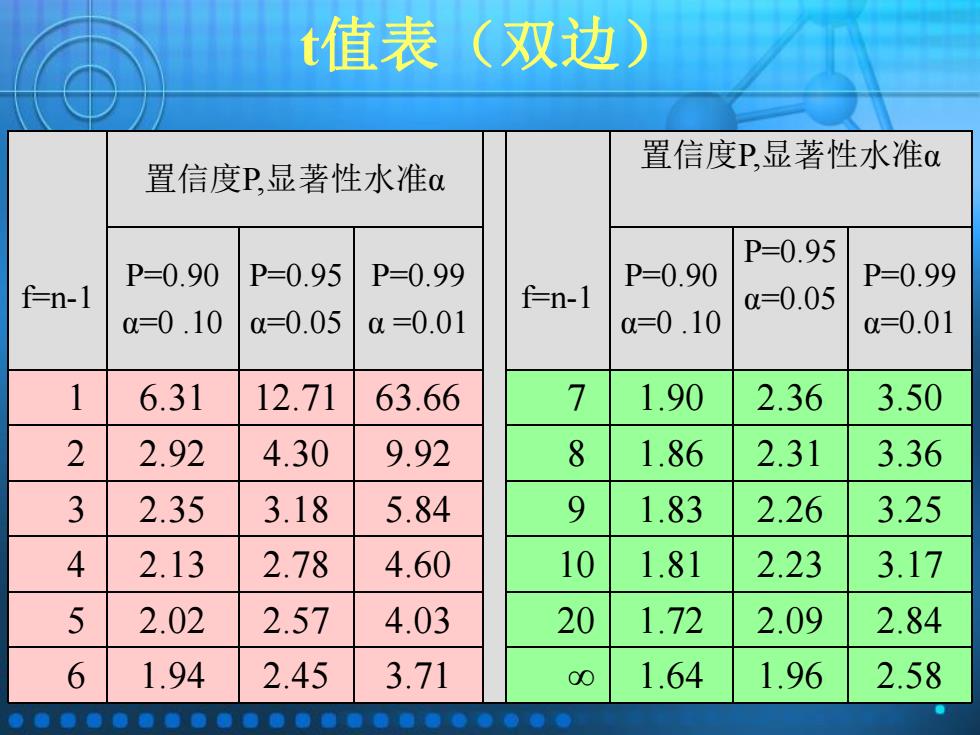
t值表(双边) f=n-1 置信度P,显著性水准α f=n-1 置信度P,显著性水准α P=0.90 α=0 .10 P=0.95 α=0.05 P=0.99 α =0.01 P=0.90 α=0 .10 P=0.95 α=0.05 P=0.99 α=0.01 1 6.31 12.71 63.66 7 1.90 2.36 3.50 2 2.92 4.30 9.92 8 1.86 2.31 3.36 3 2.35 3.18 5.84 9 1.83 2.26 3.25 4 2.13 2.78 4.60 10 1.81 2.23 3.17 5 2.02 2.57 4.03 20 1.72 2.09 2.84 6 1.94 2.45 3.71 ∞ 1.64 1.96 2.58

t值表的意义 前表为最常用的t值表。表中的P称为置信 度,表示随机测定值落在(m士s)区间内的 概率,称为显著性水准,用α表示,即 =1-P。应用表时须加脚注,注明显著性水 准和自由度,例如:t.os,g是指:置信度为 95%(显著性水准为0.05),自由度为9时 的t值
t 值表的意义 • 前表为最常用的 t 值表。表中的 P 称为置信 度,表示随机测定值落在(μ±ts)区间内的 概率,称为显著性水准,用 α 表示,即 α=1-P。应用表时须加脚注,注明显著性水 准和自由度,例如:t0.05, 9是指:置信度为 95%(显著性水准为0.05),自由度为9时 的 t 值

3)S 一平均值的标准偏差 x-u 统计量t的表达式中: S x SX称为平均值的标准偏差(平均值X与总体 平均值m相符的程度),与样本容量n有关,即: S ●●●●●
称为平均值的标准偏差(平均值 与总体 平均值μ相符的程度), 与样本容量n有关,即: -平均值的标准偏差 s x n s s x s x x t 统计量 t的表达式中: (3) X s x
(4)平均值标准偏差与测量次数的关系 1.0 从图中可见,当测 定次数n>10时,Sx 0.8 的值降低己不明显。 0.6 所以,一般的测定 0.4 平行做34次,要 0.2 求较高的56次, 10 15 20 要求更高的测定 测定次数n 平均值的标准差与测量次数的关系 做10~12次也足够 了。 ●
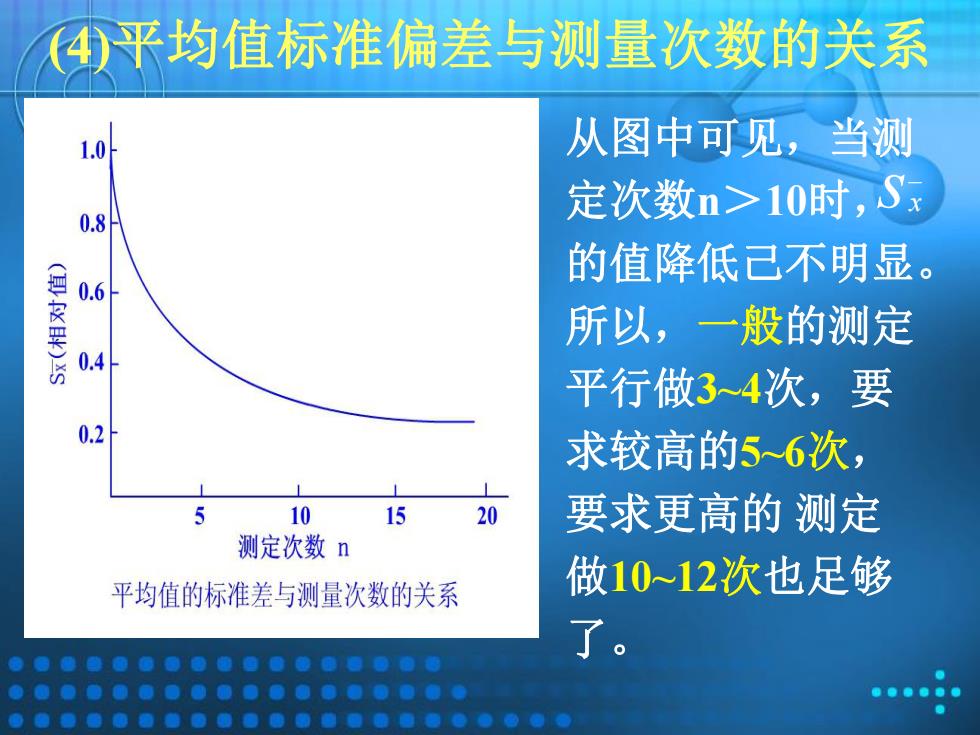
(4)平均值标准偏差与测量次数的关系 sx 从图中可见,当测 定次数n>10时, 的值降低己不明显。 所以,一般的测定 平行做3~4次,要 求较高的5~6次, 要求更高的 测定 做10~12次也足够 了

⑤)平均值与真值的关系 平均值的置信区间 用样本研究总体时,样本均值x并不等于总体 均值μ,但可以肯定,只要消除了系统误差, 在某一置信度下,一定存在着一个以样本均值 x为中心,包括总体均值Ⅱ在内的某一范围,称 为平均值的置信区间。由t的定义式得: ts u= X士 ●●●
(5)平均值与真值的关系 ——平均值的置信区间 • 用样本研究总体时,样本均值x并不等于总体 均值μ,但可以肯定,只要消除了系统误差, 在某一置信度下,一定存在着一个以样本均值 x为中心,包括总体均值 μ 在内的某一范围,称 为平均值的置信区间。由t的定义式得: n ts X