
试卷代号:1318 座位号■■ 国家开放大学(中央广播电视大学)2014年秋季学期“开放本科”期末考试 社会统计学 试题(半开卷) 2015年1月 题 号 二 三 四 总 分 分 数 得 分 评卷人 一、单项选择题(每题只有一个正确答案,请将正确答案的字母填写 在括号内。每题2分,共20分) 1.下列四种变量属于数值型变量的是( A.工资收人 B.产品等级 C.学生对考试改革的态度 D.企业的类型 2先将总体按某标志分为不同的类别或层次,然后在各个类别中采用简单随机抽样或系统 抽样的方式抽取子样本,最后将所有子样本合起来作为总样本,这样的抽样方式称为( )。 A.简单随机抽样 B.系统抽样 C.整群抽样 D.分层抽样 3.以下关于条形图的表述,不正确的是()。 A.条形图中条形的宽度是固定的 B.条形图中条形的长度(或高度)表示各类别频数的多少 C.条形图的矩形通常是紧密排列的 D.条形图通常是适用于所有类型数据 4.某校期末考试,全校语文平均成绩为80分,标准差为3分,数学平均成绩为87分,标准 差为5分。某学生语文得了83分,数学得了97分,从相对名次的角度看,该生( )的成绩 考得更好。 A.数学 B.语文 C.两门课程一样 D.无法判断 1339
试卷代号 :1318 座位号rn 国家开放大学(中央广播电视大学 )2014 年秋季学期"开放本科"期末考试 社会统计学 试题(半开卷) 2015 J 一、单项选择题(每题只有一个正确答案,请将正确答案的字母填写 在括号内。每题 分,共 20 分) 1.下列四种变量属于数值型变量的是)。 A. 工资收入 B. 产品等级 c.学生对考试改革的态度 D. 企业的类型 2. 先将总体按某标志分为不同的类别或层次,然后在各个类别中采用简单随机抽样或系统 抽样的方式抽取子样本,最后将所有子样本合起来作为总样本,这样的抽样方式称为( )。 A. 简单随机抽样 B.系统抽样 c.整群抽样 D.分层抽样 3. 以下关于条形图的表述,不正确的是)。 八.条形图中条形的宽度是固定的 B. 条形图中条形的长度(或高度)表示各类别频数的多少 c.条形图的矩形通常是紧密排列的 D. 条形图通常是适用于所有类型数据 1. 某校期末考试,全校语文平均成绩为 80 分,标准差为 分,数学平均成绩为 87 分,标准 差为 分。某学生语文得了 83 分,数学得了 97 分,从相对名次的角度看,该生)的成绩 考得更好。 A. 数学 c.两门课程一样 B. 语文 D. 无法判断 1339
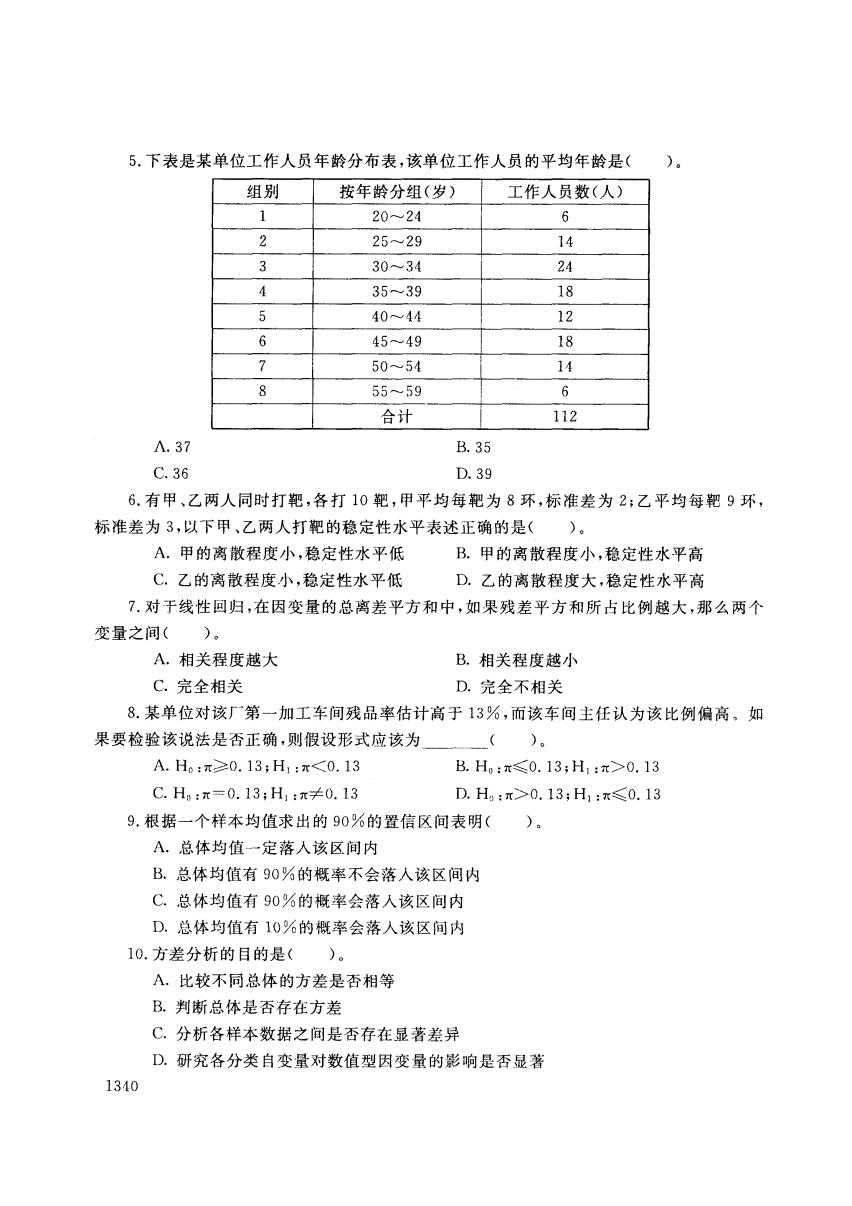
5.下表是某单位工作人员年龄分布表,该单位工作人员的平均年龄是( )。 组别 按年龄分组(岁) 工作人员数(人) 1 20~24 6 2 25~29 14 3 30~34 24 3539 18 、5 40~44 12 6 4549 18 50~54 14 8 55~59 6 合计 112 Λ.37 B.35 C.36 D.39 6.有甲、乙两人同时打靶,各打10靶,甲平均每靶为8环,标准差为2;乙平均每靶9环, 标准差为3,以下甲、乙两人打靶的稳定性水平表述正确的是( )。 A.甲的离散程度小,稳定性水平低 B.甲的离散程度小,稳定性水平高 C.乙的离散程度小,稳定性水平低 D.乙的离散程度大,稳定性水平高 7.对于线性回归,在因变量的总离差平方和中,如果残差平方和所占比例越大,那么两个 变量之间()。 A,相关程度越大 B.相关程度越小 C.完全相关 D.完全不相关 8.某单位对该厂第一加工车间残品率估计高于13%,而该车间主任认为该比例偏高,如 果要检验该说法是否正确,则假设形式应该为 ()。 A.H0:π≥0.13;H1:π0.13 C.H:π=0.13;H1:π≠0.13 D.H:r>0.13;H1:x≤0.13 9.根据一个样本均值求出的90%的置信区间表明()。 A.总体均值一定落人该区间内 B.总体均值有90%的概率不会落人该区间内 C.总体均值有90%的概率会落人该区间内 D.总体均值有10%的概率会落入该区间内 10.方差分析的目的是()。 A.比较不同总体的方差是否相等 B.判断总体是否存在方差 C.分析各样本数据之间是否存在显著差异 D.研究各分类自变量对数值型因变量的影响是否显著 1340
5. 下表是某单位工作人员年龄分布表,该单位工作人员的平均年龄是( )。 .37 C. 36 组别 1 2 3 4 D 6 7 8 按年龄分组(岁) 20~24 25~29 30~34 35~39 40~41 45~49 50~54 55~59 合计 工作人员数(人) B. 35 D.39 6 14 24 18 12 18 14 6 112 6. 有甲、乙两人同时打靶,各打 10 靶,甲平均每靶为 环,标准差为 ;乙平均每靶 环, 标准差为 ,以下甲、乙两人打靶的稳定性水平表述正确的是( )。 A. 甲的离散程度小,稳定性水平低 B. 甲的离散程度小,稳定性水平高 c.乙的离散程度小,稳定性水平低 D. 乙的离散程度大,稳定性水平高 7. 对于线性回归,在因变量的总离差平方和中,如果残差平方和所占比例越大,那么两个 变量之间( )。 A.相关程度越大 B. 相关程度越小 c.完全相关 D.完全不相关 8. 某单位对该厂第一加工车间残品率估计高于 13% ,而该车间主任认为该比例偏高。如 果要检验该说法是否正确,则假设形式应该为 A. Ho:π O. 13;H :π0.13 D. Ho:π>O.13;H :π~0.13 9. 根据一个样本均值求出的 90% 的置信区间表明( )。 A. 总体均值一定落入该区间内 B.总体均值有 90% 的概率不会落入该区间内 c.总体均值有 90% 的概率会落入该区间内 D.总体均值有 10% 的概率会落入该区间内 10. 方差分析的目的是)。 ]3.10 A. 比较不同总体的方差是否相等 B.判断总体是否存在方差 c.分析各样本数据之间是否存在显著差异 D.研究各分类自变量对数值型因变量的影响是否显著

得分 评卷人 二、名词解释(每小题5分,共20分) 11.独立样本与配对样本 12.散点图 13.二维表 14.离散系数 得分 评卷人 三、简答题(每题10分,共30分) 15.等距分组和不等距分组有什么区别?请举例说明。 ]6.简要举例说明在分析双变量的关系时,t检验和卡方检验的主要区别。 17.简述什么是简单回归分析?其作用是什么? 得分 评卷人 四、计算题(每题15分,共30分】 18.为估计每个网络用户每天上网的平均时间是多少,抽取了225个网络用户的简单随机 样本,得到样本均值为6.5个小时,样本标准差为2.5个小时。 (1)试用95%的置信水平,计算网络用户每天平均上网时间的置信区间。 (2)在所调查的225个网络用户中,年龄在20岁以下的用户为90个。以95%的置信水 平,计算年龄在20岁以下的网络用户比例的置信区间。 注:Z。.025=1.96 19.某汽车生产商欲了解广告费用(万元)对销售量(辆)的影响。收集了过去12年的有关 数据,通过分析得到:方程的截距为363,回归系数为1.42,回归平方和SSR=1600,残差平方 和SSE=450。要求: (])写出销售量y与广告费用x之间的线性回归方程。 (2)假如明年计划投入广告费用为50万,根据回归方程估计明年汽车销售量。 (3)计算判定系数R2,并解释它的意义。 1341
二、名词解释{每小题 分,共 20 分} 1.独立样本与配对样本 12. 散点图 13. 二维表 14. 离散系数 三、简答题{每题 10 分,共 30 分) 15. 等距分组和不等距分组有什么区别?请举例说明。 16. 简要举例说明在分析双变量的关系时, 检验和卡方检验的主要区别。 17. 简述什么是简单回归分析?其作用是什么? 四、计算题{每题 15 分,共 30 分} 18. 为估计每个网络用户每天上网的平均时间是多少,抽取了 225 个网络用户的简单随机 样本,得到样本均值为 6. 个小时,样本标准差为 2. 个小时。 (1)试用 95% 的置信水平,计算网络用户每天平均上网时间的置信区间。 (2) 在所调查的 225 个网络用户中,年龄在 20 岁以下的用户为 90 个。以 95% 的置信水 平,计算年龄在 20 岁以下的网络用户比例的置信区间。 注: ZC, 025 = 1. 96 19. 某汽车生产商欲了解广告费用(万元)对销售量(辆)的影响。收集了过去 12 年的有关 数据,通过分析得到:方程的截距为 363. 回归系数为1. 42. 回归平方和 SSR ',,"= 1600 ,残差平方 SSE=450 。要求: (1)写出销售量 与广告费用 之间的线性回归方程。 (2) 假如明年计划投入广告费用为 50 万,根据回归方程估计明年汽车销售量。 (3) 计算判定系数 R2 ,并解释它的意义。 1311

试卷代号:1318 国家开放大学(中央广播电视大学)2014年秋季学期“开放本科”期末考试 社会统计学 试题答案及评分标准(半开卷) (供参考) 2015年1月 一、单项选择题(每题2分,共20分) 1.A 2.D 3.C 4.A 5.D 6.B 7.B 8.A 9.C 10.D 二、名词解释(每小题5分,共20分) 11.独立样本与配对样本:独立样本是指我们得到的样本是相互独立的。(2分)配对样本 就是一个样本中的数据与另一个样本中的数据相对应的两个样本。(1分)配对样本可以消除 由于样本指定的不公平造成的差异。(2分) 12.散点图:在坐标系中,用X轴表示自变量x,用Y轴表示因变量y,而变量组(x,y)则用 坐标系中的点表示,不同的变量组在坐标系中形成不同的散点,用坐标系及其坐标系中的散点 形成的二维图就是散点图。(5分) 13.二维表:二维表就是行列交叉的表格,(1分)将两个变量一个分行排放,一个分列排 放,(1分)行列交叉处就是同属于两个变量的不同类的数据,也称为列联表。(3分) 14.离散系数:离散系数是一组数据的标准差与该组数据的均值之比,也称为变异系数。 (5分) 三、简答题(每题10分,共30分) 15.等距分组和不等距分组有什么区别?请举例说明。 (1)在对数据进行分组时,如果各组组距相等,则称为等距分组。(2分)例如,分析某班同 学期末统计课成绩时,假如最低分为73分,最高分为98分,以5分为组距进行分组,分为 70-75分,75-80分,80一85分,85-90分,90-95分,95--100分。(3分) (2)如果各组组距不相等,则称为不等距分组。(2分)例如,在分析人口时,往往将人口分 为婴幼儿组(0一6岁),少年儿童组(7一17岁),中青年组(18一59岁),老年人组(60岁及以 上),该分类中各组组距不相等,这就是不等距分组。(3分) 16.简要举例说明在分析双变量的关系时,t检验和卡方检验的主要区别。 分析双变量关系时,t检验和卡方检验都是主要用于检验这两个变量之间是否存在显著 关系。(2分)t检验主要用于对一个为数值型变量、另一个为分类变量且只有两个类别的变量 的双变量关系的统计显著性检验。(2分)卡方检验主要用于对两个分类变量之间的相关性进 行统计检验,判断变量之间是否存在显著关系。(2分) 例如,我们想考察收人与性别是否存在关系,或者两性的收人是否存在显著差异,可以用 两独立样本t检验。(2分)如果我们想考察职业与性别是否存在关系,而职业和性别都是分 类变量,那么可以用卡方检验考察不同性别之间职业是否存在显著差异。(2分) 1342
试卷代号 :1318 国家开放大学(中央广播电视大学 )2014 年秋季学期"开放本科"期末考试 社会统计学 试题答案及评分标准(半开卷) (供参考) 2015 一、单项选择题(每题 分,共 20 分) l. A 2. D 3. C 4. A 5. D 6. B 7. B 8. A 9. C 10. D 二、名词解释(每小题 分,共 20 分) 1.独立样本与配对样本:独立样本是指我们得到的样本是相互独立的。 (2 分)配对样本 就是一个样本中的数据与另一个样本中的数据相对应的两个样本。(1分)配对样本可以消除 由于样本指定的不公平造成的差异。 (2 分) 12. 散点图:在坐标系中,用 轴表示自变量 ,用 轴表示因变量 ,而变量组 (x y) 则用 坐标系中的点表示,不同的变量组在坐标系中形成不同的散点,用坐标系及其坐标系中的散点 形成的二维图就是散点图。 (5 分) 13. 二维表:二维表就是行列交叉的表格,(1分)将两个变量一个分行排放,一个分列排 放,(1分)行列交叉处就是向属于两个变量的不同类的数据,也称为列联表。 (3 分) 11. 离散系数:离散系数是一组数据的标准差与该组数据的均值之比,也称为变异系数 (5 分) 三、简答题(每题 10 分,共 30 分) 15. 等距分组和不等距分组有什么区别?请举例说明。 (1)在对数据进行分组时,如果各组组距相等,则称为等距分组。 (2 分)例如,分析某班同 学期末统计课成绩时,假如最低分为 73 分,最高分为 98 分,以 分为组距进行分组,分为 70 75 分, 75-80 分, 80一部分, 85 90 分, 90 95 分, 95-100 分。 (3 分) (2) 如果各组组距不相等,则称为不等距分组 (2 分)例如,在分析人口时,往往将人口分 为婴幼儿组 (0-6 岁) ,少年儿童组 (7-17 岁) ,中青年组 08-59 岁) ,老年人组 (60 岁及以 上) ,该分类中各组组距不相等,这就是不等距分组。 (3 分) 16. 简要举例说明在分析双变量的关系时, 检验和卡方检验的主要区别。 分析双变量关系时, 检验和卡方检验都是主要用于检验这两个变量之间是否存在显著 关系。 (2 )t 检验主要用于对一个为数值型变量、另一个为分类变量且只有两个类别的变量 的双变量关系的统计显著性检验。 (2 分)卡方检验主要用于对两个分类变量之间的相关性进 行统计检验,判断变量之间是否存在显著关系。 (2 分) 例如,我们想考察收入与性别是否存在关系,或者两性的收入是否存在显著差异,可以用 两独立样本 检验。 (2 分)如果我们想考察职业与性别是否存在关系,而职业和性别都是分 类变量,那么可以用卡方检验考察不同性别之间职业是否存在显著差异。 (2 分) 1342

17.什么是简单回归分析?其作用是什么? 简单回归分析是通过一定的数学表达式将两个变量间的线性关系进行描述,确定自变量 的变化对因变量的影响,是进行估计或预测的一种方法,侧重于考察变量之间的数量伴随关 系。(或者简单回归分析是对具有线性相关关系的两个变量之间(其中一个为自变量,另一个 为因变量)数量变化的一般关系进行分析,确定相应的数学关系式,以便进行估计或预测。) (4分) 其作用包括:(1)从已知数据出发,确定变量之间的数学关系式;(2分)(2)对变量间的关 系式进行统计检验,考察自变量是否对因变量具有显著影响;(2分)(3)利用所求出的关系式, 根据自变量的取值估计或预测因变量的取值。(2分) 四、计算题(每题15分,共30分) 18.(1)已知:n=225,x=6.5,s=2.5,Z.02s=1.96 (2分) 用户平均上网时间的95%的置信区间为: x±Z22=6.5士1.96×25=6.5±0.33 (4分) Vn v225 即(6.17,6.83)(2分) (2样本比例:P-器-0.4 (2分) 年龄在20岁以下的网络用户比例的置信区间为: Pt2A四a16X西-a4o (3分) n 225 即(33.6%,46.4%) (2分) 19.(1)回归方程为: y=363+1.42× (4分) (2)当x=50时, y=363+1.42×50=434(辆) (4分) (3)判定系数 R:=SSR SSR SST SSR +SSE =1600÷(1600+450) =0.7805 (4分) 表明在汽车销售量的总变差中,有78.05%可以由回归方程解释,说明回归方程的拟合程 度很高。(3分) 1343
17. 什么是简单回归分析?其作用是什么? 简单回归分析是通过一定的数学表达式将两个变量间的线性关系进行描述,确定自变量 的变化对因变量的影响,是进行估计或预测的一种方法,侧重于考察变量之间的数量伴随关 系。(或者简单回归分析是对具有线性相关关系的两个变量之间(其中一个为自变量,另一个 为因变量)数量变化的一般关系进行分析,确定相应的数学关系式,以便进行估计或预测。) (4 分) 其作用包括:(1)从已知数据出发,确定变量之间的数学关系式 ;(2 )(2) 对变量间的关 系式进行统计检验,考察自变量是否对因变量具有显著影响 ;(2 )(3) 利用所求出的关系式, 根据自变量的取值估计或预测因变量的取值。 (2 分) 四、计算题(每题 15 分,共 30 分) 18. (1)已知 :n=225 ,豆 =6. 5 ,s=2. 5 , 20. 025 = 1. 96 (2 分) 用户平均上网时间的 95% 的置信区间为: 王土 ZdJL=6.5±1.96 ×主;二 =6.5 0.33 (4 分) ,J /225 (6.17 6.83) (2 分) 样本比例 :p= =0.4 叫) 年龄在 20 岁以下的网络用户比例的置信区间为: IP (1 -P) _^ LL1 ^"" 10. 4X cl 0.4) /2'\i 丁土三 =0.4 士1. 96 X A / 叮叮 =0.4 0.064 (3 分) (33.6% ,46.4%) (2 分) 19. (1)回归方程为: y=363 十1. 42x (4 分) (2) x=50 时, y=363+ 1. 42X50=434( 辆) (4 分) (3) 判定系数 RZ-SSR SSR 一一- SST SSR+SSE = 1600 -;- 0600+450) =0.7805 (4 分) 表明在汽车销售量的总变差中,有 78.05% 可以由回归方程解释,说明回归方程的拟合程 度很高。 (3 分) 1343