
1.4流体流动阻力 本节重点:直管阻力与局部阻力的计算,摩擦系数的影响因素。 难燕:用因次分析法解决工程实际问题。 流动阻力的大小与流体本身的物理性质、流动状况及壁面的形状等因素有关。 化工管路系统主要由两部分组成,一部分是直管,另一部分是管件、阀门等。相应流体 流动阻力也分为两种: 直管阻力:流体流经一定直径的直管时由于内摩擦而产生的阻力: 局部阻力:流体流经管件、阀门等局部地方由于流速大小及方向的改变而引起的阻力。 1.4.1流体在直管中的流动阻力 1.阻力的表现形式 如图1-24所示,流体在水平等径直管中作定态流动。 在1-1'和2-2'截面间列柏努利方程, 8++=8*+++ 因是直径相同的水平管,4=凸= ·W,=B-卫 (1-34》 直管阻力 若管道为倾斜管,则 W,=(+8)-(g+8) (1-34a) 由此可见,无论是水平安装,还是倾斜安装,流体的流动阻力均表现为静压能的减少 仅当水平安装时,流动阳力恰好等于两截面的静压能之差。 2.直管阻力的通式 在图1-24中,对1-1'和2-2截面间流体进行受力分析: 由压力商产生的能动力方(一) 与流体流动方向相同 流体的摩擦力为 F=tA=Tl 与流体流动方向相反
1 1.4 流体流动阻力 本节重点:直管阻力与局部阻力的计算,摩擦系数的影响因素。 难点:用因次分析法解决工程实际问题。 流动阻力的大小与流体本身的物理性质、流动状况及壁面的形状等因素有关。 化工管路系统主要由两部分组成,一部分是直管,另一部分是管件、阀门等。相应流体 流动阻力也分为两种: 直管阻力:流体流经一定直径的直管时由于内摩擦而产生的阻力; 局部阻力:流体流经管件、阀门等局部地方由于流速大小及方向的改变而引起的阻力。 1.4.1 流体在直管中的流动阻力 1. 阻力的表现形式 如图 1-24 所示,流体在水平等径直管中作定态流动。 在 1-1′和 2-2′截面间列柏努利方程, Wf p z g u p z g + u + = + + + 2 2 2 2 2 1 1 1 2 1 2 1 因是直径相同的水平管, u1 = u2 1 2 z = z W p1 p2 f − = (1-34) 若管道为倾斜管,则 ( ) ( ) 2 2 1 1 z g p z g p Wf = + − + (1-34a) 由此可见,无论是水平安装,还是倾斜安装,流体的流动阻力均表现为静压能的减少, 仅当水平安装时,流动阻力恰好等于两截面的静压能之差。 2. 直管阻力的通式 在图 1-24 中,对 1-1′和 2-2′截面间流体进行受力分析: 由压力差而产生的推动力为 ( ) 4 2 1 2 d p p − 与流体流动方向相同 流体的摩擦力为 F =A =dl 与流体流动方向相反

流体在管内作定态流动,在流动方向上所受合力必定为零 (p 整理得 -P (1-35) 将式(1-35)代入式(1-34)中,得 (1-36) 将式(1,36)变形,把能量损失形,表示为动能号的某一倍数。 pu2d 2 1s8 则 (1-37) 式(1-37)为流体在直管内流动阻力的通式,称为范宁(Fanning)公式。式中1为无因 次系数,称为摩擦系数或摩擦因数,与流体流动的R爬及管壁状况有关。 根据柏努利方程的其它形式,也可写出相应的范宁公式表示式: 压头损失 (1-37a) 压力损失 9,=号 (1-37b】 值得注意的是,压力损失△p,是流体流动能量损失的一种表示形式,与两截面间的压力 差y=(P,-P2)意义不同,只有当管路为水平时,二者才相等。 应当指出,范宁公式对层流与湍流均适用,只是两种情况下摩擦系数入不同。以下对层 流与湍流时摩擦系数入分别讨论。 3.层流时的摩擦系数
2 流体在管内作定态流动,在流动方向上所受合力必定为零。 dl d p p − = 4 ( ) 2 1 2 整理得 d l p p 4 1 − 2 = (1-35) 将式(1-35)代入式(1-34)中,得 d l Wf 4 = (1-36) 将式(1-36)变形,把能量损失 W f 表示为动能 2 2 u 的某一倍数。 2 8 2 2 u d l u Wf = 令 2 8 u = 则 2 2 u d l Wf = (1-37) 式(1-37)为流体在直管内流动阻力的通式,称为范宁(Fanning)公式。式中 为无因 次系数,称为摩擦系数或摩擦因数,与流体流动的 Re 及管壁状况有关。 根据柏努利方程的其它形式,也可写出相应的范宁公式表示式: 压头损失 g u d l hf 2 2 = (1-37a) 压力损失 2 2 u d l p f = (1-37b) 值得注意的是,压力损失 p f 是流体流动能量损失的一种表示形式,与两截面间的压力 差 ( ) p = p1 − p2 意义不同,只有当管路为水平时,二者才相等。 应当指出,范宁公式对层流与湍流均适用,只是两种情况下摩擦系数 不同。以下对层 流与湍流时摩擦系数 分别讨论。 3. 层流时的摩擦系数

流体在直管中作层流流动时,管中心最大速度如式(1-35)所示。 将平均速度“=”及R=号代入上式中,可得 (B-P)=32恤 d- d (1-38) 式(1-38)称为哈根泊漫叶(Hagen-Poiscuille)方程,是流体在直管内作层流流动时压 力损失的计算式。 结合式(1-34),流体在直管内层流流动时能量损失或阻力的计算式为 A (1-39) 表明层流时阻力与速度的一次方成正比。 式(1-39)也可改写为 m,=2-64.1.-64.1. pd dpu d 2 Re d 2 (1-39a) 将式(1-39a)与式(1-37)比较,可得层流时摩擦系数的计算式 (1-40) 即层流时摩擦系数入是雷诺数Re的函数。 4.湍流时的摩擦系数 (1)因次分析法 层流时阻力的计算式是根据理论推导所得,湍流时由于情况要复杂得多,目前尚不能得 到理论计算式,但通过实验研究,可获得经验关系式,这种实验研究方法是化工中常用的方 法。在实验时,每次只能改变一个变量,而将其它变量周定,如过程涉及的变量很多,工作 量必然很大,而且将实验结果关联成形式简单便于应用的公式也很困难。若采用化工中常用 的工程研究方法一一因次分析法,可将几个变量组合成一个无因次数群(如雷诺数R即是由 d、P、u、μ四个变量组成的无因次数群),用无因次数群代替个别的变量进行实验,由于数 群的数目总是比变量的数目少,就可以大大减少实验的次数,关联数据的工作也会有所简化, 而且可将在实验室规模的小设备中用某种物料实验所得的结果应用到其它物料及实际的化工
3 流体在直管中作层流流动时,管中心最大速度如式(1-35)所示。 将平均速度 max 2 1 u = u 及 2 d R = 代入上式中,可得 1 2 2 32 ( ) d lu p p − = 2 32 d lu p f = (1-38) 式(1-38)称为哈根-泊谡叶(Hagen-Poiseuille)方程,是流体在直管内作层流流动时压 力损失的计算式。 结合式(1-34),流体在直管内层流流动时能量损失或阻力的计算式为 2 32 d lu Wf = (1-39) 表明层流时阻力与速度的一次方成正比。 式(1-39)也可改写为 Re 2 64 2 32 64 2 2 2 u d u l d l d d u lu Wf = = = (1-39a) 将式(1-39a)与式(1-37)比较,可得层流时摩擦系数的计算式 Re 64 = (1-40) 即层流时摩擦系数λ是雷诺数 Re 的函数。 4.湍流时的摩擦系数 (1)因次分析法 层流时阻力的计算式是根据理论推导所得,湍流时由于情况要复杂得多,目前尚不能得 到理论计算式,但通过实验研究,可获得经验关系式,这种实验研究方法是化工中常用的方 法。在实验时,每次只能改变一个变量,而将其它变量固定,如过程涉及的变量很多,工作 量必然很大,而且将实验结果关联成形式简单便于应用的公式也很困难。若采用化工中常用 的工程研究方法——因次分析法,可将几个变量组合成一个无因次数群(如雷诺数 Re 即是由 d、ρ、u、μ四个变量组成的无因次数群),用无因次数群代替个别的变量进行实验,由于数 群的数目总是比变量的数目少,就可以大大减少实验的次数,关联数据的工作也会有所简化, 而且可将在实验室规模的小设备中用某种物料实验所得的结果应用到其它物料及实际的化工

设备中去。 因次分析法的基础是因次一致性原则,即每一个物理方程式的两边不仅数值相等,而且 每一项都应具有相同的因次。 因次分析法的基本定理是白金汉(Buckinghan)的x定理:设影响某一物理现象的独立 变量数为n个,这些变量的基本因次数为m个,则该物理现象可用N=(一m)个独立的无因 次数群表示。 根据对摩擦阻力性质的理解和实验研究的综合分析,认为流体在湍流流动时,由于内摩 擦力而产生的压力损失△p,与流体的密度p、粘度μ、平均速度山、管径d、管长1及管壁的 粗糙度e有关,即 Apr =f(p.u.u.d.I.c) (1-41) 7个变量的因次分别为: [p]=M0L [P]=ML3 u-M8- [d]=L [=L [s]=L 【=M0-L 基本因次有3个。根据真定理,无因次数群的数目 N=n-m=7-3=4个 将式(1-41)写成幂函数的形式: Apr=kdl'upu'sl 因次关系式: M0-2L=LeLP(L0-)(ML-3)'(ML-0-1) 根据因次一致性原则: 对于M:I=d什e 对于L: -1=a+b+c-3d-e+f 对于0: -2=-c-e 设b,e,f已知,解得:
4 设备中去。 因次分析法的基础是因次一致性原则,即每一个物理方程式的两边不仅数值相等,而且 每一项都应具有相同的因次。 因次分析法的基本定理是白金汉(Buckinghan)的π定理:设影响某一物理现象的独立 变量数为 n 个,这些变量的基本因次数为 m 个,则该物理现象可用 N=(n-m)个独立的无因 次数群表示。 根据对摩擦阻力性质的理解和实验研究的综合分析,认为流体在湍流流动时,由于内摩 擦力而产生的压力损失 p f 与流体的密度ρ、粘度μ、平均速度 u 、管径 d 、管长 l 及管壁的 粗糙度ε有关,即 p f (,,u,d,l, ) f = (1-41) 7 个变量的因次分别为: [p]=M -2L -1 [ ]=ML-3 [u]=M -1 [d]=L [l]=L [ ]=L [ ]=M -1L -1 基本因次有 3 个。根据π定理,无因次数群的数目 N=n-m=7-3=4 个 将式(1-41)写成幂函数的形式: a b c d e f pf = kd l u 因次关系式: a b c d e f M L L L (L ) (ML ) (ML 1) L 2 1 1 3 1 = − − − − − − 根据因次一致性原则: 对于 M: 1= d+e 对于 L: −1 = a+b + c − 3d − e + f 对于 : − 2 = −c −e 设 b,e,f 已知,解得:

a=-b-e-f c=2-e d=1-e Ap=kdPupuel 是-) 即 兴把引 (1-42) 式中一雷诺数Rc, 一一欧拉(E)准数,也是无因次数酥· pu2 子均为简单的无因次比值,前者反碳了管于的儿何尺寸对流动阻为的影响,后者称 为相对粗精度,反映了管壁粗糙度对流动阻力的影响。 式(1:42)具体的函数关系通常由实验确定。根据实验可知,流体流动阻力与管长!成正 比,该式可改写为: 是-引 (1-43) 或 所-g-e} (1-43a) 与范宁公式(137)相对照,可得 (Re. (1-44) 即湍流时摩擦系数是Re和相对粗精度号的函数,如图125所示,称为莫秋(M00)摩 擦系数图
5 d e c e a b e f = − = − = − − − 1 2 b e f b e e e f pf kd l u − − − − − = 2 1 b e f f d d u d l k u p = − 2 即 = d d d u l u p f , , 2 (1-42) 式中 du ——雷诺数 Re, 2 u p f ——欧拉(Euler)准数,也是无因次数群。 d l 、 d 均为简单的无因次比值,前者反映了管子的几何尺寸对流动阻力的影响,后者称 为相对粗糙度,反映了管壁粗糙度对流动阻力的影响。 式(1-42)具体的函数关系通常由实验确定。根据实验可知,流体流动阻力与管长 l 成正 比,该式可改写为: = d d l u p f Re, 2 (1-43) 或 2 Re, u d d p l W f f = = (1-43a) 与范宁公式(1-37)相对照,可得 (Re, ) d = (1-44) 即湍流时摩擦系数λ是 Re 和相对粗糙度 d 的函数,如图 1-25 所示,称为莫狄(Moody)摩 擦系数图
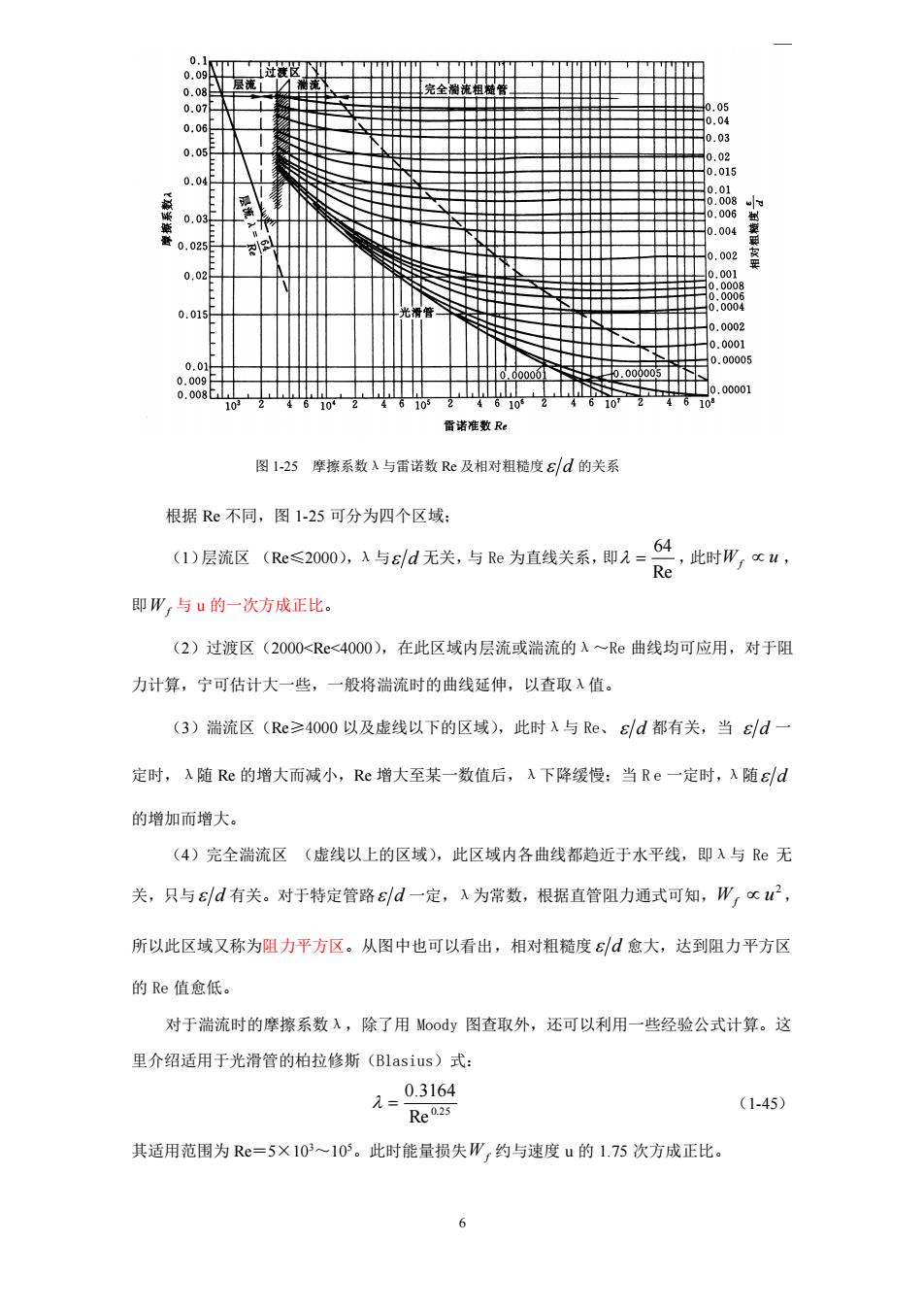
009 .01 00001 雷诺准数R。 图1-25摩擦系数λ与雷诺数Re及相对粗精度E/d的关系 根据Re不同,图1-25可分为四个区域: 层流区(≤20,1与d无关,与e为直线关系,即A-总,此时”,x。 即W,与u的一次方成正比。 (2)过渡区(2000<Re<4000),在此区域内层流或湍流的入一Re曲线均可应用,对于阻 力计算,宁可估计大一些,一般将湍流时的曲线延伸,以查取入值。 (3)湍流区(Re≥4000以及虚线以下的区域),此时X与Re、sd都有关,当sd一 定时,入随Re的增大而减小,Re增大至某一数值后,X下降缓慢:当Re一定时,入随Ed 的增加而增大。 (4)完全湍流区(虚线以上的区域),此区域内各曲线都趋近于水平线,即入与Re无 关,只与ed有关。对于特定管路ed一定,入为常数,根据直管阻力通式可知,W,c2 所以此区域又称为阻力平方区。从图中也可以看出,相对粗糙度愈大,达到阻力平方区 的Re值愈低。 对于凿流时的摩擦系数X,除了用Mooy图查取外,还可以利用一些经验公式计算。这 里介绍适用于光滑管的柏拉修斯(Blasius)式: 1-03164 (1-45) 其适用范围为Re=5X10~10。此时能量损失W,约与速度u的1.75次方成正比。 6
6 根据 Re 不同,图 1-25 可分为四个区域; (1)层流区 (Re≤2000),λ与 d 无关,与 Re 为直线关系,即 Re 64 = ,此时 Wf u , 即 W f 与 u 的一次方成正比。 (2)过渡区(2000<Re<4000),在此区域内层流或湍流的λ~Re 曲线均可应用,对于阻 力计算,宁可估计大一些,一般将湍流时的曲线延伸,以查取λ值。 (3)湍流区(Re≥4000 以及虚线以下的区域),此时λ与 Re、 d 都有关,当 d 一 定时,λ随 Re 的增大而减小,Re 增大至某一数值后,λ下降缓慢;当 R e 一定时,λ随 d 的增加而增大。 (4)完全湍流区 (虚线以上的区域),此区域内各曲线都趋近于水平线,即λ与 Re 无 关,只与 d 有关。对于特定管路 d 一定,λ为常数,根据直管阻力通式可知, 2 Wf u , 所以此区域又称为阻力平方区。从图中也可以看出,相对粗糙度 d 愈大,达到阻力平方区 的 Re 值愈低。 对于湍流时的摩擦系数λ,除了用 Moody 图查取外,还可以利用一些经验公式计算。这 里介绍适用于光滑管的柏拉修斯(Blasius)式: 0.25 Re 0.3164 = (1-45) 其适用范围为 Re=5×103~105。此时能量损失 W f 约与速度 u 的 1.75 次方成正比。 图 1-25 摩擦系数λ与雷诺数 Re 及相对粗糙度 d 的关系

考菜布鲁克(Colebrook)式 a-14-告 此式适用于湍流区的光滑管与粗糙管直至完全湍流区。 (2)管壁粗糙度对摩擦系数的影响 光滑管:玻璃管、铜管、铅管及塑料管等称为光滑管 粗糙管:钢管、铸铁管等。 管道壁面凸出部分的平均高度,称为绝对粗糙度,以£表示。绝对粗糙度与管径的比值 即d,称为相对粗糙度。工业管道的绝对粗糙度数值见教材。 管壁粗糙度对流动阻力或摩擦系数的影响,主要是由于流体在管道中流动时,流体质点 与管壁凸出部分相碰撞而增加了流体的能量损失,其影响程度与管径的大小有关,因此在摩 擦系数图中用相对粗糙度d,而不是绝对粗糙度6。 流体作层流流动时,流体层平行于管轴流动,层流层掩盖了管壁的粗糙面,同时流体的 流动速度也比较缓慢,对管壁凸出部分没有什么碰撞作用,所以层流时的流动阻力或摩擦系 数与管壁粗糙度无关,只与Re有关。 流体作湍流流动时,靠近壁面处总是存在层流内层。如果层流内层的厚度L大于管壁 的绝对粗糙度6,即6>6时,如图1-26(a)所示,此时管壁粗糙度对流动阻力的影响与层 流时相近,此为水力光滑管。随R肥的增加,层流内层的厚度逐渐减薄,当61
7 考莱布鲁克(Colebrook)式 此式适用于湍流区的光滑管与粗糙管直至完全湍流区。 (2)管壁粗糙度对摩擦系数的影响 光滑管:玻璃管、铜管、铅管及塑料管等称为光滑管; 粗糙管:钢管、铸铁管等。 管道壁面凸出部分的平均高度,称为绝对粗糙度,以 表示。绝对粗糙度与管径的比值 即 d ,称为相对粗糙度。工业管道的绝对粗糙度数值见教材。 管壁粗糙度对流动阻力或摩擦系数的影响,主要是由于流体在管道中流动时,流体质点 与管壁凸出部分相碰撞而增加了流体的能量损失,其影响程度与管径的大小有关,因此在摩 擦系数图中用相对粗糙度 d ,而不是绝对粗糙度 。 流体作层流流动时,流体层平行于管轴流动,层流层掩盖了管壁的粗糙面,同时流体的 流动速度也比较缓慢,对管壁凸出部分没有什么碰撞作用,所以层流时的流动阻力或摩擦系 数与管壁粗糙度无关,只与 Re 有关。 流体作湍流流动时,靠近壁面处总是存在着层流内层。如果层流内层的厚度δL 大于管壁 的绝对粗糙度 ,即δL> 时,如图 1-26(a)所示,此时管壁粗糙度对流动阻力的影响与层 流时相近,此为水力光滑管。随 Re 的增加,层流内层的厚度逐渐减薄,当δL< 时,如图 1-26 (b)所示,壁面凸出部分伸入湍流主体区,与流体质点发生碰撞,使流动阻力增加。当 Re 大到一定程度时,层流内层可薄得足以使壁面凸出部分都伸到湍流主体中,质点碰撞加剧, 致使粘性力不再起作用,而包括粘度μ在内的 Re 不再影响摩擦系数的大小,流动进入了完全 湍流区,此为完全湍流粗糙管。 图 1-26 流体流过管壁面的情况 = − + Re 2 18.7 1.74 2log 1 d

例分别计算下列情况下,流体流过少76×3m、长10m的水平钢管的能量损失、压头 损失及压力损失。 (1)密度为910kg、粘度为72cP的油品,流速为1.1ms: (2)20℃的水,流速为2.2m5 解:(1)油品: Re=4p-0.07x910x11=973<2000 72×10-3 流动为层流。摩擦系数可从图1-25上查取,也可用式(1-40)计算: 6464 1=Rg-00658 所以能量损失 二A0065801569k胸 0.072 压头损失 4,==569 8981=058m 压力损失 p,=plW,=910×5.69=5178Pe (2)20℃水的物性:p=998.2kgm3,4=1.005×10-3Pa:s e=4p_007x9982x22-153x10 1.005×10- 流动为湍流。求摩擦系数尚需知道相对粗糙度d,查表1-2,取钢管的绝对粗糙度8为0.2mm, 02 则 -%=00286 根据Re=1.53×10及s/d=0.00286查图1-25,得A=0.027 所以能量损失 a2=0027 072=933g 102.22 压头损失 普-8器-0 压力损失 pr=plW/=9982x9.33=9313Pa 5.非圆形管道的流动阻力 8
8 例 分别计算下列情况下,流体流过φ76×3mm、长 10m 的水平钢管的能量损失、压头 损失及压力损失。 (1) 密度为 910kg/、粘度为 72cP 的油品,流速为 1.1m/s; (2) 20℃的水,流速为 2.2 m/s。 解:(1)油品: 973 2000 72 10 0.07 910 1.1 Re 3 = = = − du 流动为层流。摩擦系数可从图 1-25 上查取,也可用式(1-40)计算: 0.0658 973 64 Re 64 = = = 所以能量损失 5.69J/kg 2 1.1 0.07 10 0.0658 2 2 2 = = = u d l Wf 压头损失 0.58m 9.81 5.69 = = = g W h f f 压力损失 = = 9105.69 = 5178Pa p f Wf (2)20℃水的物性: 3 = 998.2kg/m , 3 1.005 10− = Pa·s 5 3 1.53 10 1.005 10 0.07 998.2 2.2 = = = − du Re 流动为湍流。求摩擦系数尚需知道相对粗糙度 d ,查表1-2,取钢管的绝对粗糙度 为0.2mm, 则 0.00286 70 0.2 = = d 根据 Re=1.53×105 及 d =0.00286 查图 1-25,得λ=0.027 所以能量损失 9.33J/kg 2 2.2 0.07 10 0.027 2 2 2 = = = u d l Wf 压头损失 0.95m 9.81 9.33 = = = g W h f f 压力损失 = = 998.29.33 = 9313Pa p f Wf 5. 非圆形管道的流动阻力

对于非圆形管内的湍流流动,仍可用在圆形管内流动阻力的计算式,但需用非圆形管道 的当量直径代替圆管直径。当量直径定义为 -4 (1-46) 对于套管环隙,当内管的外径为d,外管的内径为d山时,其当量直径为 a好-d) +成4-d d.=44 对于边长分别为a、b的矩形管,其当量直径为 d.=4-ab2ab 2(a+b)a+b 在层流情况下,当采用当量直径计算阻力时,还应对式(140)进行修正,改写为 A-C (1-47) 式中C为无因次常数。 一些非圆形管的C值见教材。 注意,当量直径只用于非圆形管道流动阻力的计算,而不能用于流通面积及流速的计算。 1.4.2局部阻力 局部阻力有两种计算方法:阻力系数法和当量长度法。 1.阻力系数法 克服局部阻力所消耗的机械能,可以表示为动能的某一倍数,即 所=货 (1-48) 或 (1-48a) 式中5称为局部阻力系数,一般由实验测定。 常用管件及阀门的局部阻力系数见教材。注意表中当管截面突然扩大和突然缩小时,式 (1-48)及(1-48a)中的速度u均以小管中的速度计。 当流体自容器进入管内,5口=0.5,称为进口阻力系数:当流体自管子进入容器或从
9 对于非圆形管内的湍流流动,仍可用在圆形管内流动阻力的计算式,但需用非圆形管道 的当量直径代替圆管直径。当量直径定义为 = A de 4 =4 润湿周边 流通截面积 (1-46) 对于套管环隙,当内管的外径为 d1,外管的内径为 d2 时,其当量直径为 ( ) 2 1 2 1 2 1 2 2 4 4 d d d d d d de = − + − = 对于边长分别为 a、b 的矩形管,其当量直径为 a b ab a b ab de + = + = 2 2( ) 4 在层流情况下,当采用当量直径计算阻力时,还应对式(1-40)进行修正,改写为 Re C = (1-47) 式中 C 为无因次常数。 一些非圆形管的 C 值见教材。 注意,当量直径只用于非圆形管道流动阻力的计算,而不能用于流通面积及流速的计算。 1.4.2 局部阻力 局部阻力有两种计算方法:阻力系数法和当量长度法。 1. 阻力系数法 克服局部阻力所消耗的机械能,可以表示为动能的某一倍数,即 2 2 ' u Wf = (1-48) 或 g u hf 2 2 ' = (1-48a) 式中ζ称为局部阻力系数,一般由实验测定。 常用管件及阀门的局部阻力系数见教材。注意表中当管截面突然扩大和突然缩小时,式 (1-48)及(1-48a)中的速度 u 均以小管中的速度计。 当流体自容器进入管内, 进口 = 0.5 ,称为进口阻力系数;当流体自管子进入容器或从

管子排放到管外空间,5出口=1,称为出口阻力系数。 当流体从管子直接排放到管外空间时,管出口内侧截面上的压强可取为与管外空间相同, 但出口截面上的动能及出口阻力应与截面选取相匹配。若截面取管出口内侧,则表示流体并 未离开管路,此时截面上仍有动能,系统的总能量损失不包含出口阻力:若截面取管出口外 侧,则表示流体已经离开管路,此时截面上动能为零,而系统的总能量损失中应包含出口阻 力。由于出口阻力系数出口=1,两种选取截面方法计算结果相同。 2.当量长度法 将流体流过管件或阀门的局部阻力,折合成直径相同、长度为1,的直管所产生的阻力即 =签 (1-49) 或 6=装2 (1-49a) d 2g 式中1,称为管件或阀门的当量长度 同样,管件与阀门的当量长度也是由实验测定,有时也以管道直径的倍数L/d表示。见 教材。 1.4.3流体在管路中的总阻力 前己说明,化工管路系统是由直管和管件、阀门等构成,因此流体流经管路的总阻力应 是直管阻力和所有局部阻力之和。计算局部阻力时,可用局部阻力系数法,亦可用当量长度 法。对同一管件,可用任一种计算,但不能用两种方法重复计算。 当管路直径相同时,总阻力: Σ,=形,+m,=2号 (1-55) 或 形,=形,+形,=+头女 d2 (1-55a) 式中、1,分别为管路中所有局部阻力系数和当量长度之和。 若管路由若干直径不同的管段组成时,各段应分别计算,再加和
10 管子排放到管外空间, 出口 = 1 ,称为出口阻力系数。 当流体从管子直接排放到管外空间时,管出口内侧截面上的压强可取为与管外空间相同, 但出口截面上的动能及出口阻力应与截面选取相匹配。若截面取管出口内侧,则表示流体并 未离开管路,此时截面上仍有动能,系统的总能量损失不包含出口阻力;若截面取管出口外 侧,则表示流体已经离开管路,此时截面上动能为零,而系统的总能量损失中应包含出口阻 力。由于出口阻力系数 出口 = 1 ,两种选取截面方法计算结果相同。 2.当量长度法 将流体流过管件或阀门的局部阻力,折合成直径相同、长度为 e l 的直管所产生的阻力即 2 2 ' u d l W e f = (1-49) 或 g u d l h e f 2 2 ' = (1-49a) 式中 e l 称为管件或阀门的当量长度。 同样,管件与阀门的当量长度也是由实验测定,有时也以管道直径的倍数 l e d 表示。见 教材。 1.4.3 流体在管路中的总阻力 前已说明,化工管路系统是由直管和管件、阀门等构成,因此流体流经管路的总阻力应 是直管阻力和所有局部阻力之和。计算局部阻力时,可用局部阻力系数法,亦可用当量长度 法。对同一管件,可用任一种计算,但不能用两种方法重复计算。 当管路直径相同时,总阻力: 2 2 ' u d l Wf Wf Wf = + = + (1-55) 或 2 2 ' u d l l W W W e f f f + = + = (1-55a) 式中 、 e l 分别为管路中所有局部阻力系数和当量长度之和。 若管路由若干直径不同的管段组成时,各段应分别计算,再加和