
1流体流动 基本要求: 了解流体流动的基本规律,要求熟练掌握流体静力学基本方程、连续性方程、柏努利方 程的内容及应用,并在此基础上解决流体输送的管路计算问题。 1、举握的内容 (1)流体的密度和粘度的定义、单位、影响因素及数据的求取: (2)压强的定义、表示法及单位换算: (3)流体静力学基本方程、连续性方程、柏努利方程的内容及应用: (4)流动型态及其判断,雷诺准数的物理意义及计算: (5)流动阻力产生的原因,流体在管内流动时流动阻力(直管阻力和局部阻力)的计算: (6)简单管路的设计计算及输送能力的核算: (7)管路中流体的压力、流速及流量的测量:液柱压差计、测速管(毕托管)、孔板流 量计、转子流量计的工作原理、基本结构及计算: (8)因次分析法的原理、依据、结果及应用。 2、熟悉的内容 (1)流体的连续性和压缩性、定态流动与非定态流动 (2)层流与瑞流的特征: (3)管内流体速度分布公式及应用: (4)哈根-泊谡叶方程式的推导: (5)复杂管路计算要点: (6)正确使用各种数据图表: (7)边界层的概念。 3、了解的内容 (1)牛顿型流体与非牛顿型流体: (2)层流内层与边界层,边界层的分离。 流体是气体与液体的总称。流体流动是最普遍的化工单元操作之一,同时研究流体流动 问题也是研究其它化工单元操作的重要基础。 连续介质假定从微观讲,流体是由大量的彼此之间有一定间隙的单个分子所组成,而且 分子总是处于随机运动状态。但工程上,在研究流体流动时,常从宏观出发,将流体视为由 无数流体质点(或微团)组成的连续介质。所谓质点是指由大量分子构成的微团,其尺寸远 小于设备尺寸,但却远大于分子自由程。这些质点在流体内部紧紧相连,彼此间没有间隙
3 1 流体流动 基本要求: 了解流体流动的基本规律,要求熟练掌握流体静力学基本方程、连续性方程、柏努利方 程的内容及应用,并在此基础上解决流体输送的管路计算问题。 1、 掌握的内容 (1)流体的密度和粘度的定义、单位、影响因素及数据的求取; (2)压强的定义、表示法及单位换算; (3)流体静力学基本方程、连续性方程、柏努利方程的内容及应用; (4)流动型态及其判断,雷诺准数的物理意义及计算; (5)流动阻力产生的原因,流体在管内流动时流动阻力(直管阻力和局部阻力)的计算; (6)简单管路的设计计算及输送能力的核算; (7)管路中流体的压力、流速及流量的测量:液柱压差计、测速管(毕托管)、孔板流 量计、转子流量计的工作原理、基本结构及计算; (8)因次分析法的原理、依据、结果及应用。 2、 熟悉的内容 (1)流体的连续性和压缩性、定态流动与非定态流动; (2)层流与湍流的特征; (3)管内流体速度分布公式及应用; (4)哈根-泊谡叶方程式的推导; (5)复杂管路计算要点; (6)正确使用各种数据图表; (7)边界层的概念。 3、了解的内容 (1)牛顿型流体与非牛顿型流体; (2)层流内层与边界层,边界层的分离。 流体是气体与液体的总称。流体流动是最普遍的化工单元操作之一,同时研究流体流动 问题也是研究其它化工单元操作的重要基础。 连续介质假定 从微观讲,流体是由大量的彼此之间有一定间隙的单个分子所组成,而且 分子总是处于随机运动状态。但工程上,在研究流体流动时,常从宏观出发,将流体视为由 无数流体质点(或微团)组成的连续介质。所谓质点是指由大量分子构成的微团,其尺寸远 小于设备尺寸,但却远大于分子自由程。这些质点在流体内部紧紧相连,彼此间没有间隙, (9)流体的密 度和粘度 的定义、单 位、影响因 素及数据 的求取; (10) 压强的 定义、表示 法及单位 换算; (11) 流体静 力学基本 方程、连续 性方程、柏 努利方程 的内容及 应用; (12) 流动型 态及其判 断,雷诺准 数的物理 意义及计 算; (13) 流动阻 力产生的 原因,流体 在管内流 动时流动 阻力(直管 阻力和局 部阻力)的 计算; (14) 简单管

即流体充满所占空间,为连续介质。 流体主要特征具有流动性:无固定形状,随容器形状而变化:受外力作用时内部产生相 对运动。 流体种类如果流体的体积不随压力变化而变化,该流体称为不可压缩性流体:若随压力 发生变化,则称为可压缩性流体。一般液体的体积随压力变化很小,可视为不可压缩性流体: 而对于气体,当压力变化时,体积会有较大的变化,常视为不可压缩性流体,但如果压力的 变化率不大时,该气体也可当作不可压缩性流体处理。 1.1流体静力学 本节重点:静力学基本方程式及其应用。 难点:U形压差计的测量。 1.1.1密度 单位体积流体的质量,称为流体的密度,表达式为 p-W (1-1 式中P一一流体的密度,kgm3: m一一流体的质量,kg: —流体的体积,m。 对一定的流体,其密度是压力和温度的函数,即 P=f(p.T) 液体密度通常液体可视为不可压缩流体,认为其密度仅随温度变化(极高压力除外), 其变化关系可由手册中查得。 气体密度对于气体,当压力不太高、温度不太低时,可按理想气体状态方程计算 (1-2) 式中P一气体的绝对压力,Pa: M一一气体的摩尔质量,kg/mol: T一一绝对温度,K:
4 即流体充满所占空间,为连续介质。 流体主要特征 具有流动性;无固定形状,随容器形状而变化;受外力作用时内部产生相 对运动。 流体种类 如果流体的体积不随压力变化而变化,该流体称为不可压缩性流体;若随压力 发生变化,则称为可压缩性流体。一般液体的体积随压力变化很小,可视为不可压缩性流体; 而对于气体,当压力变化时,体积会有较大的变化,常视为不可压缩性流体,但如果压力的 变化率不大时,该气体也可当作不可压缩性流体处理。 1.1 流体静力学 本节重点:静力学基本方程式及其应用。 难点:U 形压差计的测量。 1.1.1 密度 单位体积流体的质量,称为流体的密度,表达式为 V m = (1-1) 式中 ρ——流体的密度,kg/m3; m——流体的质量,kg; V——流体的体积,m3。 对一定的流体,其密度是压力和温度的函数,即 = f ( p,T) 液体密度 通常液体可视为不可压缩流体,认为其密度仅随温度变化(极高压力除外), 其变化关系可由手册中查得。 气体密度 对于气体,当压力不太高、温度不太低时,可按理想气体状态方程计算 RT pM = (1-2) 式中 p——气体的绝对压力,Pa; M——气体的摩尔质量,kg/mol; T——绝对温度,K;

R-一气体常数,其值为8.314J/(mol.K) 一般在手册中查得的气体密度都是在一定压力与温度下的,若条件不同,则密度需进行 换算。 化工生产中遇到的流体,大多为几种组分构成的混合物,而通常手册中查得的是纯组分 的密度,混合物的平均密度Pm可以通过纯组分的密度进行计算。 液体混合物的密度对于液体混合物,其组成通常用质量分率表示。假设各组分在混合 前后体积不变,则有 1=+++0 (1-3) P.PP: 式中4,a…a。一一液体混合物中各组分的质量分率 P,P2…Pn一一各纯组分的密度,kgm。 气体混合物的密度对于气体混合物,其组成通常用体积分率表示。各组分在混合前后 质量不变,则有 Pm=P4+P92+…+Pnpn (1-4) 式中真,真。一一气体混合物中各组分的体积分率。 气体混合物的平均密度P也可利用式(1-2)计算,但式中的摩尔质量M应用混合气体 的平均摩尔质量Mm代替,即 (1-5) RI 而 Mm=My+M2y2+…+Mnyn (1-6 式中M1,M2…Mn一一各纯组分的摩尔质量,kg/mol: ,乃…y。—气体混合物中各组分的摩尔分率。 对于理想气体,其摩尔分率y与体积分率中相同。 比容单位质量流体具有的体积,是密度的倒数,单位为mkg。 v- m p
5 R——气体常数,其值为 8.314 J/(mol·K)。 一般在手册中查得的气体密度都是在一定压力与温度下的,若条件不同,则密度需进行 换算。 化工生产中遇到的流体,大多为几种组分构成的混合物,而通常手册中查得的是纯组分 的密度,混合物的平均密度ρm可以通过纯组分的密度进行计算。 液体混合物的密度 对于液体混合物,其组成通常用质量分率表示。假设各组分在混合 前后体积不变,则有 n n m a a a = + ++ 2 2 1 1 1 (1-3) 式中 a1 a2 an , ——液体混合物中各组分的质量分率; 1 2 n , ——各纯组分的密度,kg/m3。 气体混合物的密度 对于气体混合物,其组成通常用体积分率表示。各组分在混合前后 质量不变,则有 m = 11 + 1 2 ++ n n (1-4) 式中 1 2 n , ——气体混合物中各组分的体积分率。 气体混合物的平均密度 m 也可利用式(1-2)计算,但式中的摩尔质量 M 应用混合气体 的平均摩尔质量 Mm代替,即 RT pMm m = (1-5) 而 m n n M = M y + M y ++ M y 1 1 2 2 (1-6) 式中 M1 M2 Mn , ——各纯组分的摩尔质量,kg/mol; n y y y 1 2 , ——气体混合物中各组分的摩尔分率。 对于理想气体,其摩尔分率 y 与体积分率φ相同。 比容 单位质量流体具有的体积,是密度的倒数,单位为 m3 /kg。 1 = = m V v

1.1.2压力 流体垂直作用于单位面积上的力,称为流体的静压强,简称压强,习惯上又称为压力。 在静止流体中,作用于任意点不同方向上的压力在数值上均相同。 压力的单位在SI单位中,压力的单位是N/m2,称为帕斯卡,以Pa表示。此外,压力 的大小也间接地以流体柱高度表示,如用米水柱或毫米汞柱等。若流体的密度为P,则液柱 高度h与压力p的关系为 p=pgh (1-7) 注意:用液柱高度表示压力时,必须指明流体的种类,如600mmHg,10mH:0等。 标准大气压有如下换算关系: 1am=1.013×105Pa=760mmHg=10.33mH0 压力的表示方法压力的大小常以两种不同的基准来表示:一是绝对真空:另一是大气 压力。基准不同,表示方法也不同。以绝对真空为基准测得的压力称为绝对压力,是流体的 真实压力:以大气压为基准测得的压力称为表压或真空度。 表压=绝对压力·大气压力 表压 P 真空度=大气压力·绝对压力 大气压 绝对压力与表压、真空度的关系如图11所示。 绝对压力 真空度 一般为避免混淆,通常对表压、真空度等加以标注 绝对压力 如2000Pa(表压),10mmHg(真空度)等,还应指明当 绝对直空 地大气压力。 1.1.3流体静力学平衡方程 图川绝对压力、表压与真空度的关系 1.静力学基本方程 如图1-2所示,容器内装有密度为ρ的液体,液体可认为是不可压缩流体,其密度不随压 力变化。在静止液体中取一段液柱,其截面积为A,以容器底面为基准水平面,液柱的上、 下端面与基准水平面的垂直距离分别为:,和2·作用在上、下两端面的压力分别为P和P2。 重力场中在垂直方向上对液柱进行受力分析: (1)上端面所受总压力P=P,A,方向向下: (2)下端面所受总压力B=P2A,方向向上: 6 图1-2液柱受力分析
6 1.1.2 压力 流体垂直作用于单位面积上的力,称为流体的静压强,简称压强,习惯上又称为压力。 在静止流体中,作用于任意点不同方向上的压力在数值上均相同。 压力的单位 在 SI 单位中,压力的单位是 N/m2,称为帕斯卡,以 Pa 表示。此外,压力 的大小也间接地以流体柱高度表示,如用米水柱或毫米汞柱等。若流体的密度为 ,则液柱 高度 h 与压力 p 的关系为 p = gh (1-7) 注意:用液柱高度表示压力时,必须指明流体的种类,如 600mmHg,10mH2O 等。 标准大气压有如下换算关系: 1atm = 1.013×105Pa =760mmHg =10.33m H2O 压力的表示方法 压力的大小常以两种不同的基准来表示:一是绝对真空;另一是大气 压力。基准不同,表示方法也不同。以绝对真空为基准测得的压力称为绝对压力,是流体的 真实压力;以大气压为基准测得的压力称为表压或真空度。 表压 = 绝对压力 - 大气压力 真空度 =大气压力 - 绝对压力 绝对压力与表压、真空度的关系如图 1-1 所示。 一般为避免混淆,通常对表压、真空度等加以标注, 如 2000Pa(表压),10mmHg(真空度)等,还应指明当 地大气压力。 1.1.3 流体静力学平衡方程 1. 静力学基本方程 如图 1-2 所示,容器内装有密度为 的液体,液体可认为是不可压缩流体,其密度不随压 力变化。在静止液体中取一段液柱,其截面积为 A ,以容器底面为基准水平面,液柱的上、 下端面与基准水平面的垂直距离分别为 1 z 和 2 z 。作用在上、下两端面的压力分别 为 1 p 和 2 p 。 重力场中在垂直方向上对液柱进行受力分析: (1)上端面所受总压力 P1 = p1A ,方向向下; (2)下端面所受总压力 P2 = p2A ,方向向上; 绝对真空 大气压 绝对压力 绝对压力 表压 真空度 p1 p2 图 1-1 绝对压力、表压与真空度的关系

(3)液柱的重力G=P343,-22),方向向下。 液柱处于静止时,上述三项力的合力应为零,即 P2A-PA-Pg4(31-22)=0 整理并消去A,得 P=P+P8(1-2) 压力形式 (1-8) 变形得 A+8=合+8 能量形式 (1-8a) 若将液柱的上端面取在容器内的液面上,设液面上方的压力为P。,液柱高度为h,则式 (1-8)可改写为 P2=P。+Pgh (1-8b) 式(1-8)、式(1-8a)及式(1-8b)均称为静力学基本方程。 静力学基本方程适用于在重力场中静止、连续的同种不可压缩流体,如液体。而对于气 体来说,密度随压力变化,但若气体的压力变化不大,密度近似地取其平均值而视为常数时, 式(1-8、式(1-8a)及式(1-8b)也适用。 讨论: (1)在静止的、连续的同种液体内,处于同一水平面上各点的压力处处相等。压力相等 的面称为等压面。 (2)压力具有传递性:液面上方压力变化时,液体内部各点的压力也将发生相应的变化。 (2)式1-8a)中,8、分别为单位质量流体所具有的位能和静压能,此式反映出 在同一静止流体中,处在不同位置流体的位能和静压能各不相同,但总和恒为常量。因此。 静力学基本方程也反映了静止流体内部能量守恒与转换的关系。 (3)式(1-8b)可改写为 p:-Ps=h 说明压力或压力差可用液柱高度表示,此为前面介绍压力的单位可用液柱高度表示的依 据。但需注明液体的种类。 >
7 (3)液柱的重力 ( ) 1 2 G = gA z − z , 方向向下。 液柱处于静止时,上述三项力的合力应为零,即 p2A− p1A− gA(z1 − z2 ) = 0 整理并消去 A,得 ( ) 2 1 1 2 p = p + g z − z 压力形式 (1-8) 变形得 z g p z g p 2 2 1 1 + = + 能量形式 (1-8a) 若将液柱的上端面取在容器内的液面上,设液面上方的压力为 a p ,液柱高度为 h ,则式 (1-8)可改写为 p2 = pa + gh (1-8b) 式(1-8)、式(1-8a)及式(1-8b)均称为静力学基本方程。 静力学基本方程适用于在重力场中静止、连续的同种不可压缩流体,如液体。而对于气 体来说,密度随压力变化,但若气体的压力变化不大,密度近似地取其平均值而视为常数时, 式(1-8)、式(1-8a)及式(1-8b)也适用。 讨论: (1)在静止的、连续的同种液体内,处于同一水平面上各点的压力处处相等。压力相等 的面称为等压面。 (2)压力具有传递性:液面上方压力变化时,液体内部各点的压力也将发生相应的变化。 (2)式(1-8a)中, zg 、 p 分别为单位质量流体所具有的位能和静压能,此式反映出 在同一静止流体中,处在不同位置流体的位能和静压能各不相同,但总和恒为常量。因此, 静力学基本方程也反映了静止流体内部能量守恒与转换的关系。 (3)式(1-8b)可改写为 h g p pa = − 2 说明压力或压力差可用液柱高度表示,此为前面介绍压力的单位可用液柱高度表示的依 据。但需注明液体的种类

2.静力学基本方程的应用 利用静力学基本原理可以测量流体的压力、容器中液位及计算液封高度等。 (1)压力及压力差的测量 1)U形压差计 U形压差计的结构如图13所示。它是一根U形玻璃管,内装指示液。要求指示液与被 测流体不互溶,不起化学反应,且其密度大于被测流体密度。常用的指示液有水银、四氯化 碳、水和液体石蜡等,应根据被测流体的种类和测量范围合理选择指示液。 当用U形压差计测量设备内两点的压差时,可将U形管两端与被测两点直接相连,利用R 的数值就可以计算出两点间的压力差。 P 设指示液的密度为P。,被测流体的密度为 p。由图13可知,A和A'点在同一水平面上, 且处于连通的同种静止流体内,因此,A和A'点 的压力相等,即P4=P财: 而 P.=P+Pog(m+R) P=p:+pgm+PogR 图1-3U形压差计 所以 P+Pog(m+R)=p2 pgm+pogR 整理得P-P2=(P-P)gR (1-9) 若被测流体是气体,由于气体的密度远小于指示剂的密度,即P一p≈P,则式(19) 可简化为 P1-P2≈RgPo (1-9a) U形压差计也可测量流体的压力,测量时将U形管一端与被测点连接,另一端与大气相 通,此时测得的是流体的表压或真空度。 思考:若将U形压差计安装在倾斜管路中,此时读数R反映了什么? P-P:=(Po-p)gR+(=2-=)8
8 2. 静力学基本方程的应用 利用静力学基本原理可以测量流体的压力、容器中液位及计算液封高度等。 (1)压力及压力差的测量 1)U 形压差计 U 形压差计的结构如图 1-3 所示。它是一根 U 形玻璃管,内装指示液。要求指示液与被 测流体不互溶,不起化学反应,且其密度大于被测流体密度。常用的指示液有水银、四氯化 碳、水和液体石蜡等,应根据被测流体的种类和测量范围合理选择指示液。 当用 U 形压差计测量设备内两点的压差时,可将 U 形管两端与被测两点直接相连,利用 R 的数值就可以计算出两点间的压力差。 设指示液的密度为 0 ,被测流体的密度为 。由图 1-3 可知,A 和 A′点在同一水平面上, 且处于连通的同种静止流体内,因此,A 和 A′点 的压力相等,即 ' A A p = p , 而 ( ) pA = p1 + 0 g m + R p p gm gR A ' = 2 + + 0 所以 p1 + 0 g(m + R) = p2 + gm + 0 gR 整理得 p1 − p2 = (0 − )gR (1-9) 若被测流体是气体,由于气体的密度远小于指示剂的密度,即 0 − 0 ,则式(1-9) 可简化为 p1 − p2 Rg 0 (1-9a) U 形压差计也可测量流体的压力,测量时将 U 形管一端与被测点连接,另一端与大气相 通,此时测得的是流体的表压或真空度。 思考:若将 U 形压差计安装在倾斜管路中,此时读数 R 反映了什么? p1 − p2 = (0 − )gR + (z2 − z1 )g

例如附图所示,水在水平管道内流动。为测量流体在某截面处的压力,直接在该处连 接一U形压差计,指示液为水银,读数R=250mm,h=900mm。己知当地大气压为101.3张Pa, 水的密度p=1000kgm3,水银的密度P,=13600kgm2 试计算该截面处的压力。 解:图中AA'面间为静止、连续的同种流体,且处于同 水平面,因此为等压面,即P4=P 而Px=P。 Pa=p+pgm+PogR 于是 P。=p+Pgm+PogR 则截面处绝对压力 p=P。-Pgm-P8gR =101300-1000×9.81×0.9-13600×9.81×0.25 =59117Pa 或直接计算该处的真空度 P。-p=Pgm+PogR =1000×9.81×0.9+13600×9.81×0.25 =42183Pa 由此可见,当U形管一端与大气相通时,U形压差计实际反映的就是该处的表压或真空 度。 U形压差计在使用时为防止水银蒸汽向空气中扩散,通常在与大气相通的一侧水银液面上 充入少量水,计算时其高度可忽略不计。 例如附图所示,水在管道中流动。为测得A-A'、B-B藏面的压力差,在管路上方安 装一U形压差计,指示液为水银。已知压差计的读数R=150mm,试计算A-A'、B-B'截面 的压力差。已知水与水银的密度分别为1000kgm3和13600kgm3。 解:图中,1-1'面与2-2面间为静止、连续的同种流体,且处于同一水平面,因此为等 压面,即 P1=P, P2=P2 Py=PA-Pgm -X
9 例 如附图所示,水在水平管道内流动。为测量流体在某截面处的压力,直接在该处连 接一 U 形压差计,指示液为水银,读数 R=250mm,h=900mm。已知当地大气压为 101.3kPa, 水的密度 = 1000 kg/m3,水银的密度 0 =13600 kg/m3。 试计算该截面处的压力。 解:图中 A-A′面间为静止、连续的同种流体,且处于同一 水平面,因此为等压面,即 ' A A p = p 而 p A ' = pa pA = p + gm + 0 gR 于是 pa = p + gm + 0 gR 则截面处绝对压力 59117Pa 101300 1000 9.81 0.9 13600 9.81 0.25 0 = = − − p = pa − gm − gR 或直接计算该处的真空度 42183Pa 1000 9.81 0.9 13600 9.81 0.25 0 = = + pa − p = gm + gR 由此可见,当 U 形管一端与大气相通时,U 形压差计实际反映的就是该处的表压或真空 度。 U 形压差计在使用时为防止水银蒸汽向空气中扩散,通常在与大气相通的一侧水银液面上 充入少量水,计算时其高度可忽略不计。 例 如附图所示,水在管道中流动。为测得 A-A′、B-B′截面的压力差,在管路上方安 装一 U 形压差计,指示液为水银。已知压差计的读数 R=150mm,试计算 A-A′、B-B′截面 的压力差。已知水与水银的密度分别为 1000kg/m3 和 13600 kg/m3。 解:图中,1-1′面与 2-2′面间为静止、连续的同种流体,且处于同一水平面,因此为等 压面,即 ' 1 1 p = p , ' 2 2 p = p 又 p 1 = pA − gm 1
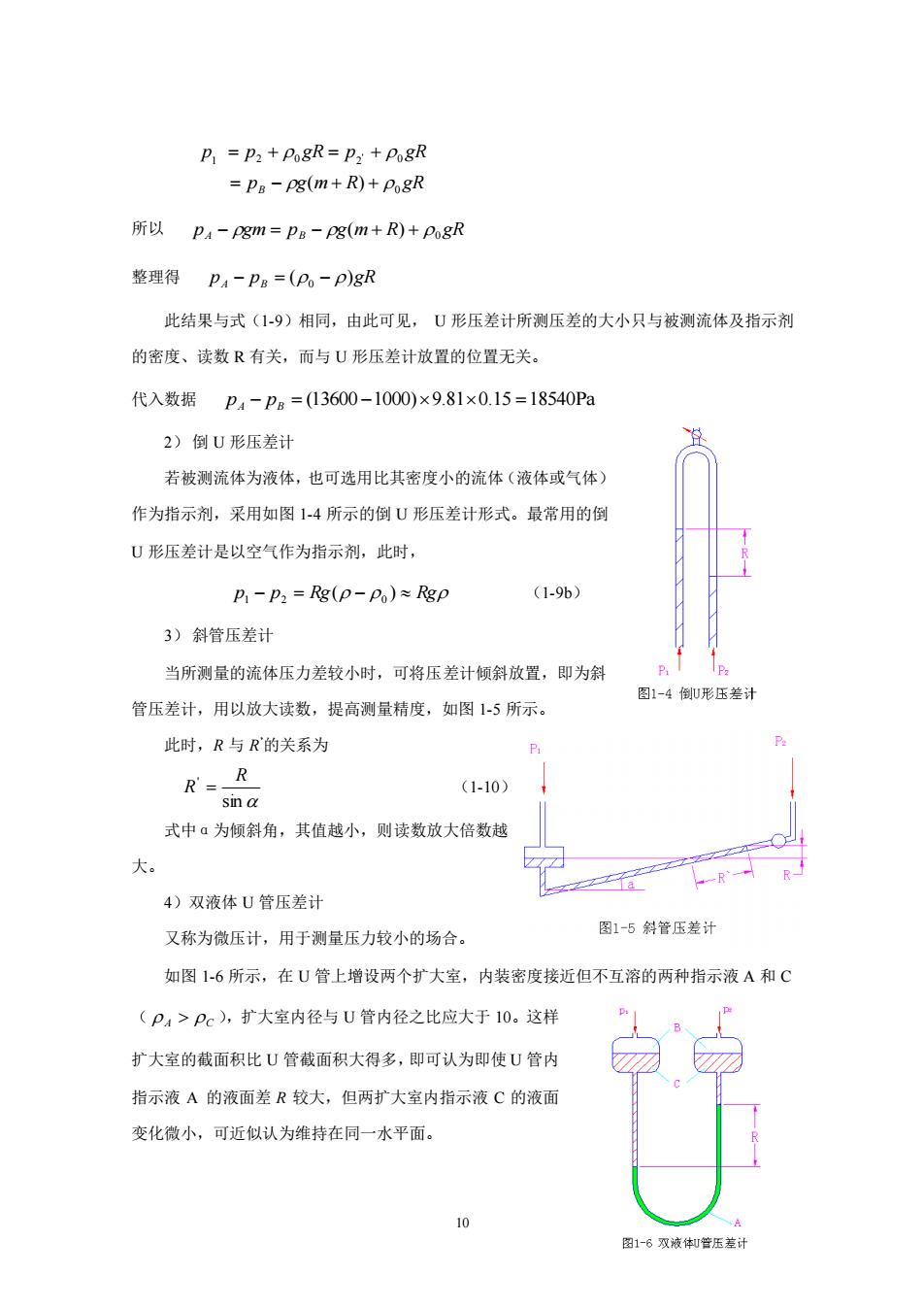
P=P:+PogR=p:+pogR =Pa-pg(m+R)+PogR 所以PA4-Pgm=PB-Pg(m+R)+PogR 整理得P4-Pg=(P-P)gR 此结果与式(19)相同,由此可见,U形压差计所测压差的大小只与被测流体及指示剂 的密度、读数R有关,而与U形压差计放置的位置无关。 代入数据p4-Pm=13600-1000)×9.81×0.15=18540Pa 2)倒U形压差计 若被测流体为液体,也可选用比其密度小的流体(液体或气体) 作为指示剂,采用如图14所示的倒U形压差计形式。最常用的倒 U形压差计是以空气作为指示剂,此时, B-P2=Rg(p-P)≈Rgp (1-9b) 3)斜管压差计 当所测量的流体压力差较小时,可将压差计倾斜放置,即为斜 图1-4倒U形压差计 管压差计,用以放大读数,提高测量精度,如图15所示。 此时,R与R的关系为 R品 (1-10) 式中ā为倾斜角,其值越小,则读数放大倍数越 大。 4)双液体U管压差计 又称为微压计,用于测量压力较小的场合。 图1-5斜管压差计 如图1-6所示,在U管上增设两个扩大室,内装密度接近但不互溶的两种指示液A和C (P>P),扩大室内径与U管内径之比应大于10。这样 扩大室的截面积比U管截面积大得多,即可认为即使U管内 指示液A的液面差R较大,但两扩大室内指示液C的液面 变化微小,可近似认为维持在同一水平面。 图1-8双液体知管压差计
10 p g m R gR p p gR p gR B 0 1 2 0 2 0 ( ) ' = − + + = + = + 所以 pA − gm = pB − g(m + R) + 0 gR 整理得 pA − pB = (0 − )gR 此结果与式(1-9)相同,由此可见, U 形压差计所测压差的大小只与被测流体及指示剂 的密度、读数 R 有关,而与 U 形压差计放置的位置无关。 代入数据 − = (13600 −1000)9.810.15 =18540Pa pA pB 2) 倒 U 形压差计 若被测流体为液体,也可选用比其密度小的流体(液体或气体) 作为指示剂,采用如图 1-4 所示的倒 U 形压差计形式。最常用的倒 U 形压差计是以空气作为指示剂,此时, p1 − p2 = Rg( − 0 ) Rg (1-9b) 3) 斜管压差计 当所测量的流体压力差较小时,可将压差计倾斜放置,即为斜 管压差计,用以放大读数,提高测量精度,如图 1-5 所示。 此时,R 与 R ’的关系为 sin ' R R = (1-10) 式中α为倾斜角,其值越小,则读数放大倍数越 大。 4)双液体 U 管压差计 又称为微压计,用于测量压力较小的场合。 如图 1-6 所示,在 U 管上增设两个扩大室,内装密度接近但不互溶的两种指示液 A 和 C ( A C ),扩大室内径与 U 管内径之比应大于 10。这样 扩大室的截面积比 U 管截面积大得多,即可认为即使 U 管内 指示液 A 的液面差 R 较大,但两扩大室内指示液 C 的液面 变化微小,可近似认为维持在同一水平面

于是有 P-P:Rg(Pa-Pc) (1-11) 由上式可知,只要选择两种合适的指示液,使(Pp4一P)较小,就可以保证较大的读数R 例用U形压差计测量某气体流经水平管道两截面的压力差,指示液为水,密度为 1000kgm3,读数R为12mm。为了提高测量精度,改为双液体U管压差计,指示液A为含 40%乙醇的水溶液,密度为920kgm,指示液C为煤油,密度为850kgm3。间读数可以放大 多少倍?此时读数为多少? 解:用U形压差计测量时,被测流体为气体,可根据式(1-9)计算 P-P2≈gP 用双液体U管压差计测量时,可根据式(1-11)计算 P-P:=Rg(Pa-Pe) 因为所测压力差相同,联立以上二式,可得放大倍数 Po 1000 Rp-A920-850=143 此时双液体U管的读数为 R-14.3R-14.3×12-171.6mm (2)液位测量 在化工生产中,经常要了解容器内液体的贮存量,或对 设备内的液位进行控制,因此,常常需要测量液位。测量液 位的装置较多,但大多数遵循流体静力学基本原理。 图1-7所示的是利用U形压差计进行近距离液位测量装 置。在容器或设备1的外边设一平衡室2,其中所装的液体 与容器中相同,液面高度维持在容器中液面允许到达的最高 位置。用一装有指示剂的U形压差计3把容器和平衡室连 通起米,压差计读数R即可指示出容器内的液面高度,关系为 11
11 于是有 ( ) p1 − p2 = Rg A − C (1 -11) 由上式可知,只要选择两种合适的指示液,使 ( ) A − C 较小,就可以保证较大的读数 R。 例 用 U 形压差计测量某气体流经水平管道两截面的压力差,指示液为水,密度为 1000kg/m3,读数 R 为 12mm。为了提高测量精度,改为双液体 U 管压差计,指示液 A 为含 40%乙醇的水溶液,密度为 920 kg/m3,指示液 C 为煤油,密度为 850 kg/m3。问读数可以放大 多少倍?此时读数为多少? 解:用 U 形压差计测量时,被测流体为气体,可根据式(1-9a)计算 p1 − p2 Rg 0 用双液体 U 管压差计测量时,可根据式(1-11)计算 ( ) ' p1 − p2 = R g A − C 因为所测压力差相同,联立以上二式,可得放大倍数 14.3 920 850 0 1000 ' = − = − = R A C R 此时双液体 U 管的读数为 14.3 14.3 12 171.6mm ' R = R = = (2)液位测量 在化工生产中,经常要了解容器内液体的贮存量,或对 设备内的液位进行控制,因此,常常需要测量液位。测量液 位的装置较多,但大多数遵循流体静力学基本原理。 图1-7所示的是利用U形压差计进行近距离液位测量装 置。在容器或设备 1 的外边设一平衡室 2,其中所装的液体 与容器中相同,液面高度维持在容器中液面允许到达的最高 位置。用一装有指示剂的 U 形压差计 3 把容器和平衡室连 通起来,压差计读数 R 即可指示出容器内的液面高度,关系为
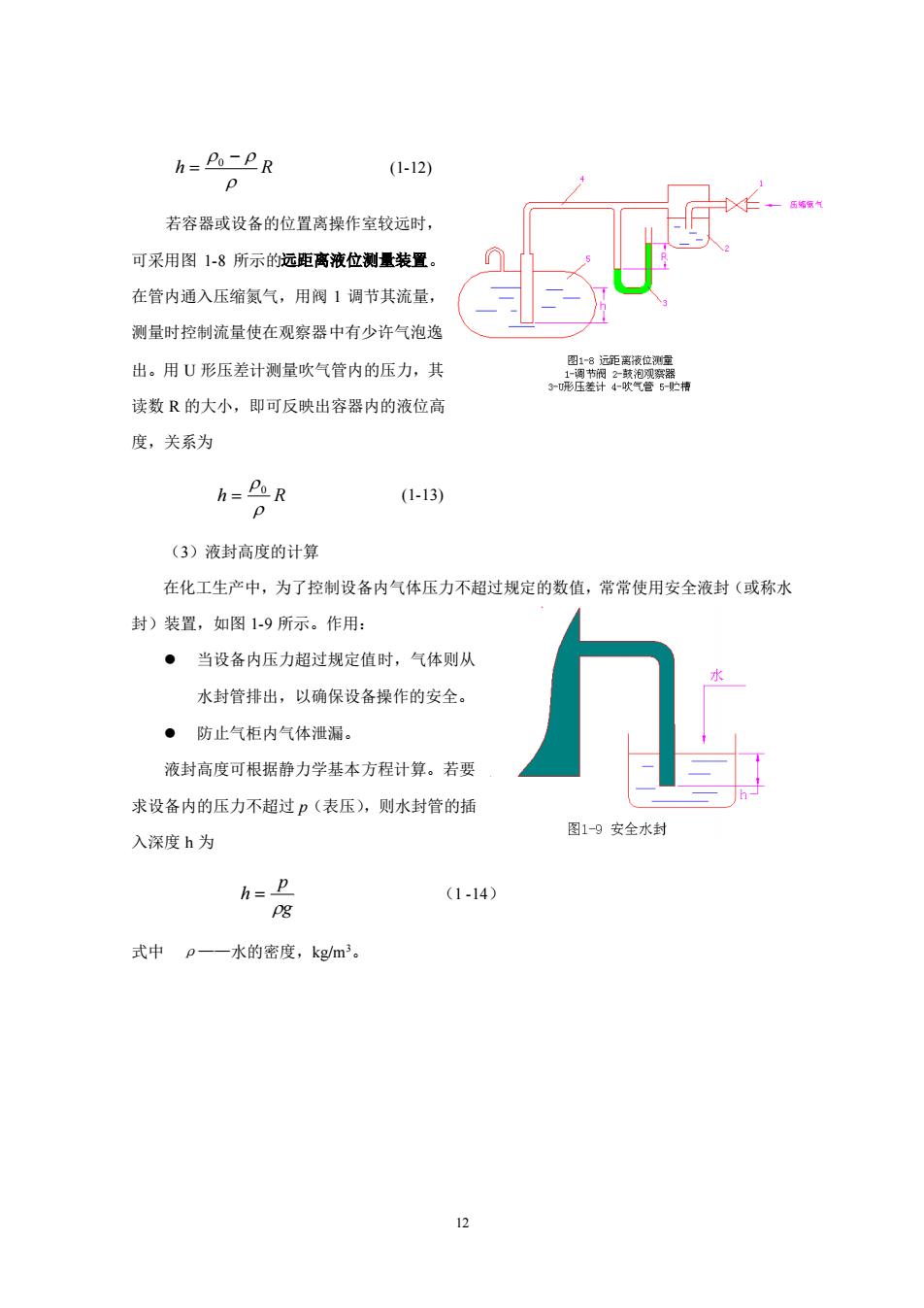
h-BpeR (1-12) 若容器或设备的位置离操作室较远时, 可采用图1-8所示的远距高液位测量装置。 在管内通入压缩氨气,用阀1调节其流量, 测量时控制流量使在观察器中有少许气泡逸 出。用U形压差计测量吹气管内的压力,其 读数R的大小,即可反映出容器内的液位高 度,关系为 A-合R (1-13) (3)液封高度的计算 在化工生产中,为了控制设备内气体压力不超过规定的数值,常常使用安全液封(或称水 封)装置,如图19所示。作用: ·当设备内压力超过规定值时,气体则从 水封管排出,以确保设备操作的安全。 ·防止气柜内气体泄漏。 液封高度可根据静力学基本方程计算。若要 求设备内的压力不超过p(表压),则水封管的插 入深度h为 图1-9安全水封 h=P (1-14) 式中p-一水的密度,kgm3
12 h R − = 0 (1-12) 若容器或设备的位置离操作室较远时, 可采用图 1-8 所示的远距离液位测量装置。 在管内通入压缩氮气,用阀 1 调节其流量, 测量时控制流量使在观察器中有少许气泡逸 出。用 U 形压差计测量吹气管内的压力,其 读数 R 的大小,即可反映出容器内的液位高 度,关系为 h R 0 = (1-13) (3)液封高度的计算 在化工生产中,为了控制设备内气体压力不超过规定的数值,常常使用安全液封(或称水 封)装置,如图 1-9 所示。作用: ⚫ 当设备内压力超过规定值时,气体则从 水封管排出,以确保设备操作的安全。 ⚫ 防止气柜内气体泄漏。 液封高度可根据静力学基本方程计算。若要 求设备内的压力不超过 p(表压),则水封管的插 入深度 h 为 g p h = (1 -14) 式中 ρ——水的密度,kg/m3