4.4传热过程的计算 在实际生产中,需要冷热两种流体进行热交换,但不允许它们混合,为此需要采用间壁式的换 热器。此时,冷 ,两流体间的热交换包括了固体壁面的 和流 贸失装的该作款:关于手和对流格热在前面已个时本节主安在武装避上进一少时论制 4.4.1总传热系数和总传热速率方程 一、总传热速率方程 间壁两侧流体的热交换过程包括如下三个串联的传热过程。流体在换热器中沿管长方向的温度 分布 为dA微元壁内、外流体 【(平均温度), 位财通 前已述及,两流体的热交换过程由三个串联的传热过程组成: 管外对流: de, (T-T.) 管壁热传导:d0=6d4(亿,-1) 管内对流 d03=a3d420.-0 对于稳定传热 do=do=do:=do 0=-1=7-4=-1 T-1 与d0=KdT-),即d0=T-对比,得 KdA 式中 K——总传热系数,w/m2K。 讨论 1.当传热面为平面时,dA=dA=dA=A,则:+ 如此规定) =++或是 式中 K1 以换热管的外表面为基准的总传热系数: dm 一换热管的对数平均直径,d,=d-d)
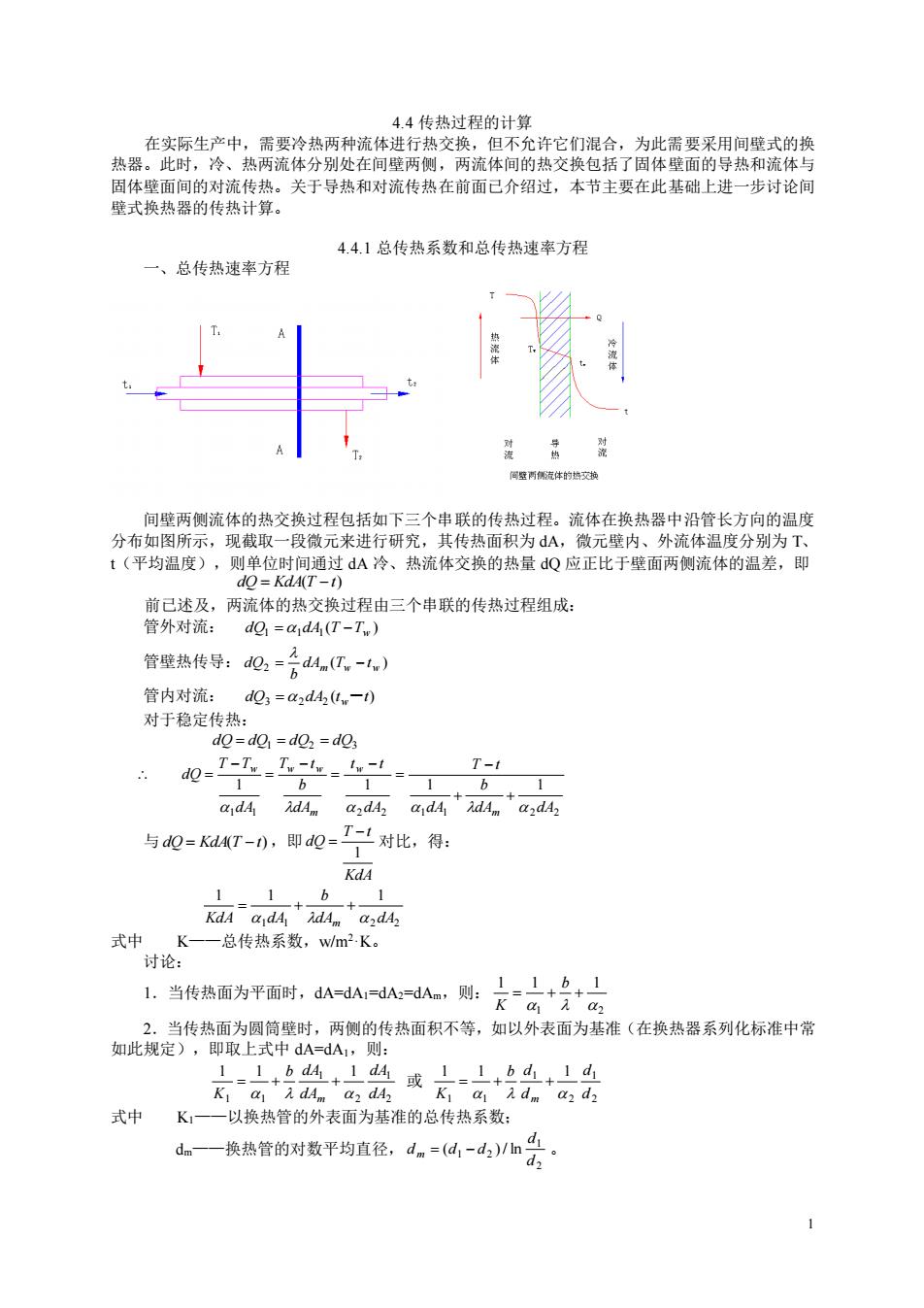
1 4.4 传热过程的计算 在实际生产中,需要冷热两种流体进行热交换,但不允许它们混合,为此需要采用间壁式的换 热器。此时,冷、热两流体分别处在间壁两侧,两流体间的热交换包括了固体壁面的导热和流体与 固体壁面间的对流传热。关于导热和对流传热在前面已介绍过,本节主要在此基础上进一步讨论间 壁式换热器的传热计算。 4.4.1 总传热系数和总传热速率方程 一、总传热速率方程 间壁两侧流体的热交换过程包括如下三个串联的传热过程。流体在换热器中沿管长方向的温度 分布如图所示,现截取一段微元来进行研究,其传热面积为 dA,微元壁内、外流体温度分别为 T、 t(平均温度),则单位时间通过 dA 冷、热流体交换的热量 dQ 应正比于壁面两侧流体的温差,即 dQ = KdA(T −t) 前已述及,两流体的热交换过程由三个串联的传热过程组成: 管外对流: ( ) dQ1 =1dA1 T −Tw 管壁热传导: ( ) 2 m w w dA T t b dQ = − 管内对流: ( ) 3 2 2 dQ dA t t = w- 对于稳定传热: dQ = dQ1 = dQ2 = dQ3 1 1 2 2 1 1 2 2 1 1 1 1 dA dA b dA T t dA t t dA b T t dA T T dQ m w m w w w + + − = − = − = − = 与 dQ = KdA(T −t) ,即 KdA T t dQ 1 − = 对比,得: 1 1 2 2 1 1 1 dA dA b KdA dA m = + + 式中 K——总传热系数,w/m2·K。 讨论: 1.当传热面为平面时,dA=dA1=dA2=dAm,则: 1 2 1 1 1 = + + b K 2.当传热面为圆筒壁时,两侧的传热面积不等,如以外表面为基准(在换热器系列化标准中常 如此规定),即取上式中 dA=dA1,则: 2 1 2 1 1 1 1 1 1 dA dA dA b dA K m = + + 或 2 1 2 1 1 1 1 1 1 d d d b d K m = + + 式中 K1——以换热管的外表面为基准的总传热系数; dm——换热管的对数平均直径, 2 1 1 2 ( ) / ln d d d m = d − d

以内表面为茶指:方女受安女 对于薄层圆筒壁<2,近似用平壁计算(误差<4%,工程计算可接受)。 d, 不翻是指经来费教得的0无医对0:灯一刊分,因为天和T一的具有同部作风能板 分有困难。为此,可以将该式中K取整个换热器的平均值K,(T一t)也取为整个换热器上的平均 为分中K为平均传热系数:L为平约温度 值△tm,则积分 换热器使用一段时间后,传热速率会下降,这往往是由于传热表面有污垢积存的缘故,污垢 的存在增加了传热热阻。虽然此层污垢不厚,由于其导热系数小,热阻大,在计算K值时不可忽略。 通常根据经验直接估计污垢热阻值,将其考虑在K中,即 式中 -传热面两侧的污垢热阻,m2·KW 为消除污垢热阻的影响,应定期清洗换热器。 4.42热量衡算式和传热速率方程间的关系 、,T t,he 热良好,热损失可以忽 换 换热器时, 冷流体吸收热。 (1)无相变 T2.Hi Q=Gcp(T-T2)=G2cm(t2-h) 热流体 或Q=G,(H1-H2)=G2(h2-) Gi,Cpt,Ti,Ht 冷流体 G2.Cp2.ti.h Q=Glr+c(T -T=G2cp241-2) 式中Q一流体放出或吸收的热量,J⅓: 一流体的汽化潜热,kJg: 和 热负荷是由生 艺系件决定的 ,是对换热器换热能力的要求:而传热速率是换热器本身在 定操作条件下的 身的特 换热器时,通常 西过 。而在实际设 因此,传热过程计算的基础是传热速 方程和热量 衡算式。 4.43平均温差的计算 前己述及,在沿管长方向的不同部分,冷、热流体温度差不同,本节讨论如何计算其平均值4 就冷、热流体的相互流动方向而言,可以有不同的流动型式,传热平均温差△的计算方法因流动型
2 以内表面为基准: 2 2 1 2 2 1 1 1 1 = + + d m b d d d K 以壁表面为基准: 1 1 2 2 1 1 1 d b d d d K m m m = + + 对于薄层圆筒壁 2 1 d d <2,近似用平壁计算(误差<4%,工程计算可接受)。 3.1/K 值的物理意义: 2 1 2 1 1 1 1 1 1 d d d b d K m = + + 二、总传热速率方程 若想求出整个换热器的 Q,需要对 dQ = KdA(T −t) 积分,因为 K 和(T-t)均具有局部性,因此积 分有困难。为此,可以将该式中 K 取整个换热器的平均值 K,(T-t)也取为整个换热器上的平均 值tm,则积分结果如下:Q=KAtm 此式即为总传热速率方程;式中 K 为平均总传热系数;tm为平均温度差。 三、污垢热阻 换热器使用一段时间后,传热速率 Q 会下降,这往往是由于传热表面有污垢积存的缘故,污垢 的存在增加了传热热阻。虽然此层污垢不厚,由于其导热系数小,热阻大,在计算 K 值时不可忽略。 通常根据经验直接估计污垢热阻值,将其考虑在 K 中,即 2 1 2 2 1 2 1 1 1 1 1 1 d d d d R d b d R K m = + + + + 式中 R1、R2——传热面两侧的污垢热阻,m2·K/W。 为消除污垢热阻的影响,应定期清洗换热器。 4.4.2 热量衡算式和传热速率方程间的关系 如图所示的换热过程,冷、热流体的 进、出口温度分别为 t1、t2,T1、T2,冷、 热流体的质量流量为 G1、G2。设换热器绝 热良好,热损失可以忽略,则两流体流经 换热器时,单位时间内热流体放出热等于 冷流体吸收热。 (1)无相变 ( ) ( ) 1 1 1 2 2 2 2 1 Q G c T T G c t t = p − = p − 或 ( ) ( ) Q = G1 H1 − H2 = G2 h2 − h1 (2)有相变 若热流体有相变化,如饱和蒸汽冷凝, 而冷流体无相变化,如下式所示: [ ( )] ( ) 1 1 2 2 2 1 2 Q G r c T T G c t t = + p s − = p − 式中 Q ──流体放出或吸收的热量,J/s; r ──流体的汽化潜热,kJ/kg; Ts──饱和蒸汽温度(=T1)。 热负荷是由生产工艺条件决定的,是对换热器换热能力的要求;而传热速率是换热器本身在一 定操作条件下的换热能力,是换热器本身的特性,二者是不相同的。 对于一个能满足工艺要求的换热器,其传热速率值必须等于或略大于热负荷值。而在实际设计 换热器时,通常将传热速率和热负荷数值上认为相等,通过热负荷可确定换热器应具有的传热速率, 再依据传热速率来计算换热器所需的传热面积。因此,传热过程计算的基础是传热速率方程和热量 衡算式。 4.4.3 平均温差的计算 前已述及,在沿管长方向的不同部分,冷、热流体温度差不同,本节讨论如何计算其平均值tm, 就冷、热流体的相互流动方向而言,可以有不同的流动型式,传热平均温差tm的计算方法因流动型 热流体 G1,Cp1,T1,H1 冷流体 G2,Cp2,t1,h1 t2,h2 T2,H2

式而异。按照参与热交换的冷热流体在沿换热器传热面流动时,各点温度变化情况,可分为恒温差 传热和变温差传热。 间壁的 液休 相变 商下泰发:而间壁的另一侧,创 温庄 N=T-1 变温 度随 换热器位置而 的情况 间壁 专热过程叶 侧的流体 1.单侧变温 如用蒸汽加热一冷流体,蒸汽冷凝放出潜热,冷凝温度T不变,而冷流体的温度从上升到口 或者热流体温度从T下降T,放出显热去加热另一较低温度1下沸腾的液体,后者温度始终保持在 沸点t。 2 式。 逆流 并流 错流 折流 (1)逆流和并流 传热面么 并流:参与换热的两种流体沿传热面平行而同向的流动。 逆流:参与换热的两种流体沿传热面平行而反向的流体。 沿传热面的局部温度差(T-)是变化的,所以在计算传热速率时必须用积分的方法求出整个传 热面上的平均温度差△tm。下面以逆流操作(两侧流体无相变)为例,推导A的计算式。 如图所示,热流体的质量流量G,比热容c,进出口温度为T、T2:冷流体的质量流量G2, 比热容cp2,进出口温度为t、t2 定装dC为整过 在如下 及沿传热为定值 现取换 典器中 失元段为研究对象,其传热面积为dA,在d内热流体因放出热量湿度下降 3
3 式而异。按照参与热交换的冷热流体在沿换热器传热面流动时,各点温度变化情况,可分为恒温差 传热和变温差传热。 一、恒温差传热 恒温差传热:两侧流体均发生相变,且温度不变,则冷热流体温差处处相等,不随换热器位置 而变的情况。如间壁的一侧液体保持恒定的沸腾温度 t 下蒸发;而间壁的另一侧,饱和蒸汽在温度 T 下冷凝过程,此时传热面两侧的温度差保持均一不变,称为恒温差传热。 二、变温差传热 变温差传热是指传热温度随换热器位置而变的情况。当间壁传热过程中一侧或两侧的流体。沿 着传热壁面在不同位置点温度不同,因此传热温度差也必随换热器位置而变化,该过程可分为单侧 变温和双侧变温两种情况。 1.单侧变温 如用蒸汽加热一冷流体,蒸汽冷凝放出潜热,冷凝温度 T 不变,而冷流体的温度从 t1 上升到 t2。 或者热流体温度从 T1 下降 T2,放出显热去加热另一较低温度 t 下沸腾的液体,后者温度始终保持在 沸点 t。 2.双侧变温 此时平均温度差tm与换热器内冷热流体流动方向有关,下面先来介绍工业上常见的几种流动型 式。 逆流 并流 错流 折流 (1)逆流和并流 并流:参与换热的两种流体沿传热面平行而同向的流动。 逆流:参与换热的两种流体沿传热面平行而反向的流体。 沿传热面的局部温度差(T-t)是变化的,所以在计算传热速率时必须用积分的方法求出整个传 热面上的平均温度差tm。下面以逆流操作(两侧流体无相变)为例,推导tm的计算式。 如图所示,热流体的质量流量 G1,比热容 cp1,进出口温度为 T1、T2;冷流体的质量流量 G2, 比热容 cp2,进出口温度为 t1、t2。 在如下假定条件下(稳定传热过程): 1)稳定操作,G1,G2 为定值; 2)cp1、cp2 及 K 沿传热面为定值; 3)换热器无损失。 现取换热器中一微元段为研究对象,其传热面积为 dA,在 dA 内热流体因放出热量温度下降 dT, t =T − t

冷流体因吸收热量温度升高dt,传热量为dQ。 dA段热量衡算的微分式:dQ=Gcp1dT=G2cp2d dA段传热速率方程的微分式:d=K(T-)d4 dQ=GcpdT==K(T-1)dA T d(T-1) KT-A-GenGGG) d(r (a) 逆流:7出==万- i1←t2 边界条件: A=0时,M1=T1-2 A=A时,2=T2-4 代入式(a)中,得: ka-p d(T-1) (T-IX1/GCpl -1/G2cp2) d M(1/GICpl-1/G2Cm2) KA=01Gc -Gc) (b) 对整个换热器做热量衡算:Q=Gcn1(红-T2)=G,cp22-4) 1 Q·G2c =。代入®)中 h4马 山n=-出2」 对数平均温差。 讨论 2)习按蛋松是从逆流推导来的只也用于并流 将较 记为△ ,则可用算术平均值代普品+,2(误差<4%,工程计算可接受) 4)当A=At,Mm=M,=2 在大多数的列管换热器中,两流体并非荷单的逆流或并流,因为传热的好坏,除考虑温度差的一 影响 数的多 构是杏紧凑合理等。所以实怀上两近 两种流 流体只流 动,另一流体反复来回折流:或者两流体都反复折回 舞杂读些情税流突的含o0d和Boam提出的图算法〔也可采用理论求解L的计算式, 流 几种洁动刑式 但形式太复杂)
4 冷流体因吸收热量温度升高 dt,传热量为 dQ。 dA 段热量衡算的微分式: dQ G c dT G c dt = 1 p1 = 2 p2 dA 段传热速率方程的微分式: dQ = K(T −t)dA dQ = G1 c p1dT = G2 c p2dt = K(T −t)dA(1/ 1/ ) ( ) 1/ 1/ ( ) 1 p1 2 p2 1 p1 2 p2 G c G c d T t G c dt G c dT K T t dA − − = − − − = = 分离变量: (1/ 1/ ) ( ) 1/ 1/ ( ) 1 p1 2 p2 1 p1 2 p2 G c G c d T t G c dt G c dT K T t dA − − = − − − = = (a) 逆流: 1 2 1 2 1 1 2 2 2 1 t t T T t T t t T t → = − = − 边界条件: A=0 时, 1 1 2 t =T −t A=A 时, 2 2 1 t = T −t 代入式(a)中,得: (1/ 1/ ) ( )(1/ 1/ ) ( ) 1 1 2 2 1 1 2 2 0 2 1 2 1 p p t t p p t t A t G c G c d t T t G c G c d T t KdA − = − − − = 2 1 1 1 2 2 ln (1/ 1/ ) 1 t t G c G c KA p p − = (b) 对整个换热器做热量衡算: ( ) ( ) 1 1 1 2 2 2 2 1 Q G c T T G c t t = p − = p − 得: Q t t Q G c T T G c p p 2 1 2 2 1 2 1 1 1 ; 1 − = − = 代入(b)中 Q t t KA Q T t T t KA Q T T t t KA t t 1 2 2 1 1 2 2 1 1 2 2 1 ( ) ( ) ( ) ( ) ln − = − − − = − − − = KA tm t t t t Q KA = − = 2 1 1 2 ln 2 1 1 2 ln t t t t tm − = ——对数平均温差。 讨论: 1)上式虽然是从逆流推导来的,但也适用于并流。 2)习惯上将较大温差记为t1,较小温差记为t2; 3)当t1/t2<2,则可用算术平均值代替 tm = (t1 + t2 )/ 2 (误差<4%,工程计算可接受) 4)当t1=t2, 1 2 tm = t =t (2)错流和折流 在大多数的列管换热器中,两流体并非简单的逆流或并流,因为传热的好坏,除考虑温度差的 大小外,还要考虑到影响传热系数的多种因素以及换热器的结构是否紧凑合理等。所以实际上两流 体的流向,是比较复杂的多程流动,或是相互垂直的交叉流动。 错流:两种流体的流向垂直交叉。 折流:一流体只沿一个方向流动,另一流体反复来回折流;或者两流体都反复折回。 复杂流:几种流动型式的组合。 对于这些情况,通常采用 Underwood 和 Bowan 提出的图算法(也可采用理论求解tm的计算式, 但形式太复杂)

I)先按逆流计算对数平均温差△tme, 2)求平均温差校正系数p =f(P,R) P=4 冷流体温升 T-11 两流体最初温差 R=I-五。热流体温降 ”=冷流体温升 查图→0 3)求平均传热温差△ym=m 平均温差校正系数 1,这是由于在列管换热器内增设了折流挡板及采用多管程,传 得换热的冷 热流体在换热器内呈折流或错流,导致实际平均传热温差恒低于纯逆流时的平均传热温 三、流向的选择 1.如前所述的各种流动型式,逆流和并流可以看成是两种极端情况。在流体进出口温度相同的 条件下,逆流的平均温差最大,并流最小,其它流动型式的△介于两者之间。从提高传热推动力来 言,逆流最佳。 I)在热负荷Q、K相同时,采用逆流可以较小的传热面积A完成相同的换热任务: 2)在热负荷Q、A相同时,可以节省加热和冷却介质的用量或多回收热。 )逆流 体间的温度差较为均匀。 物质知上 要求加热温度不高于某 (并流 ):或者易固化 冷 的是为 提高传热系 易于 传执面 ,综合利弊 最好 >0.9,绝不能使 0.8,否则另外选其他流型 4.当换热器一侧流体发生相变,可能其温度保持不变,此时就无所谓逆并流,不论何种流动形 式,只要进出口温度相同,则△均相等。 44壁温的计算 克传热系数(如自 的计算中都需要知道 时 知道壁温。下 对于稳态传热:Q=KA△n= 利用上面的公式计算壁温,得: Tr =T--9 讨论 般换热器金属壁的大,即b/Am小,热阻小,tw=Tw: 2.当w, ,说明传热面两侧的温度差之比等于两侧热阻之比,即哪侧 热阻大温差大:如a>a,得:(T-Tr)<( ),Tw接近于工,即α大热阻小侧流体的温度。 3.如果两侧有污垢,还应考虑污垢热阻的影响。 0=KAM= 7-7w --k..-_ tw-I +R2) 例颗:欲在直立式单程列管换热器的壳程将流率为035水s,温度为80C的南和苯蒸汽冷凝并 冷却到30C,苯在80心C时的冷凝热为394n 的出执头为1 P℃。换热器由38根直径为 2,长为2的无鞋钢管组成,未恭爱在管外冷传热茶色0w。流苯在 对流传热系数a2=1200Wm2.C,冷却水在管内与苯逆流流动,其温度由20°C升至30°℃,试计算: 5
5 1)先按逆流计算对数平均温差tm 逆, 2)求平均温差校正系数 冷流体温升 热流体温降 = 两流体最初温差 冷流体温升 = − − = − − = = 2 1 1 2 1 1 2 1 ( , ) t t T T R T t t t P f P R 3)求平均传热温差 tm = tm逆 平均温差校正系数0.9,绝不能使 <0.8,否则另外选其他流型。 4.当换热器一侧流体发生相变,可能其温度保持不变,此时就无所谓逆并流,不论何种流动形 式,只要进出口温度相同,则tm均相等。 4.4.4 壁温的计算 在热损失和某些对流传热系数(如自然对流、强制层流、冷凝、沸腾等)的计算中都需要知道 壁温。此外选择换热器类型和管材时,也需要知道壁温。下面来看壁温的计算。 对于稳态传热: 1 1 2 2 1 1 A t t A b T t A T T Q KA t w m W w W m − = − = − = = 利用上面的公式计算壁温,得: 1A1 Q TW T = − ; m W W A bQ t T = − ; 2 A2 Q tW t = + 讨论: 1.一般换热器金属壁的大,即 b/Am小,热阻小,tW=TW; 2.当 tW=TW,得 2 2 1 1 1/ 1/ A A T t T T W W = − − ,说明传热面两侧的温度差之比等于两侧热阻之比,即哪侧 热阻大温差大;如 1 2 ,得: (T −TW ) (TW −t),TW 接近于 T,即大热阻小侧流体的温度。 3.如果两侧有污垢,还应考虑污垢热阻的影响。 2 2 1 2 1 1 1 ) 1 ( 1 ) 1 ( A R t t A b T t A R T T Q KA t w m W w W m + − = − = + − = = 例题:欲在直立式单程列管换热器的壳程将流率为 0.35kg/s,温度为 80C 的饱和苯蒸汽冷凝并 冷却到 30C,苯在 80C 时的冷凝热为 394kJ/kg,液苯的比热为 1.8kJ/kg.C。换热器由 38 根直径为 25×2.5mm,长为 2m 的无缝钢管组成,苯蒸汽在管外冷凝传热系数1=1400W/m2 .C,液苯在管外 对流传热系数2=1200W/m2 .C,冷却水在管内与苯逆流流动,其温度由 20C 升至 30C,试计算: 查图

(1)冷却水的用量:(钢的导热系数=45W/mC) (2)如管内水的对流传热系数为1717Wm2.C,问该换热器是否能满足要求? 例愿:用120C的他和水汽将流量为6mh的装稀滨液在双管程列首换热器中从温度为80 [p ,且以管外考 2800 1)换热婴所需的管长 (2)操作一年后,由于污垢积累,溶液侧的污垢系数增加了0.00009m2.CW,若维持溶液原流 量及进口温度,其出口温度为多少?若又保证溶液原出口温度,可采取什么措施?(定性说明) 溶液的p=1000kg/m3:cp=4.2kkg.C
6 (1)冷却水的用量;(钢的导热系数=45W/m.C) (2)如管内水的对流传热系数为 1717W/m2 .C,问该换热器是否能满足要求? 例题:用 120C 的饱和水蒸汽将流量为 36m3 /h 的某稀溶液在双管程列管换热器中从温度为 80C 上升到 95C,每程有直径为25×2.5mm 管子 30 根,且以管外表面积为基准 K=2800 W/m2 .C,蒸汽 侧污垢热阻和管壁热阻可忽略不计。求: (1)换热器所需的管长; (2)操作一年后,由于污垢积累,溶液侧的污垢系数增加了 0.00009m2 .C/W,若维持溶液原流 量及进口温度,其出口温度为多少?若又保证溶液原出口温度,可采取什么措施?(定性说明) 溶液的=1000kg/m3;cp=4.2kJ/kg. C