
1.6流速与流量的测量 本节重点:孔板流量计与转子流量计的原理、特点等。 难点:流量方程的推导。 1.61测速管 测速度的结构与测量原理测速管又称皮托(Po)管,如图1-31所示,是由两根弯成 直角的同心套管组成,内管管口正对者管道中流体流动方向,外管的管口是封闭的,在外管 前端壁面四周开有若干测压小孔。为了减小误差,测速管的前端经常做成半球形以减少涡流。 测速管的内管与外管分别与U形压差计相连。 内管所测的是流体在A处的局部动能和静压能之和,称为冲压能。 内管A处: 台+ 由于外管壁上的测压小孔与流体流动方向平行,所以外管仅测 得流体的静压能,即 外管B处: U形压差计实际反映的是内管冲压能和外管静压能之差,即 告g-g-哈-8 图1-31测速管 则该处的局部速度为 (1-62) 将U形压差计公式(1-9)代入,可得 u=、 2Rg(Po-P) (1-62a)
1 1.6 流速与流量的测量 本节重点: 孔板流量计与转子流量计的原理、特点等。 难点: 流量方程的推导。 1.6.1 测速管 测速度的结构与测量原理 测速管又称皮托(Pitot)管,如图 1-31 所示,是由两根弯成 直角的同心套管组成,内管管口正对着管道中流体流动方向,外管的管口是封闭的,在外管 前端壁面四周开有若干测压小孔。为了减小误差,测速管的前端经常做成半球形以减少涡流。 测速管的内管与外管分别与 U 形压差计相连。 内管所测的是流体在 A 处的局部动能和静压能之和,称为冲压能。 内管 A 处: . 2 2 1 u pA p = + 由于外管壁上的测压小孔与流体流动方向平行,所以外管仅测 得流体的静压能,即 外管 B 处: pB p = U 形压差计实际反映的是内管冲压能和外管静压能之差,即 . 2 . 2 2 1 ) 2 1 ( u p u p pA pB p = − = + − = 则该处的局部速度为 p u = 2 . (1-62) 将 U 形压差计公式(1-9)代入,可得 2 ( ) 0 . − = Rg u (1-62a) 图 1-31 测速管
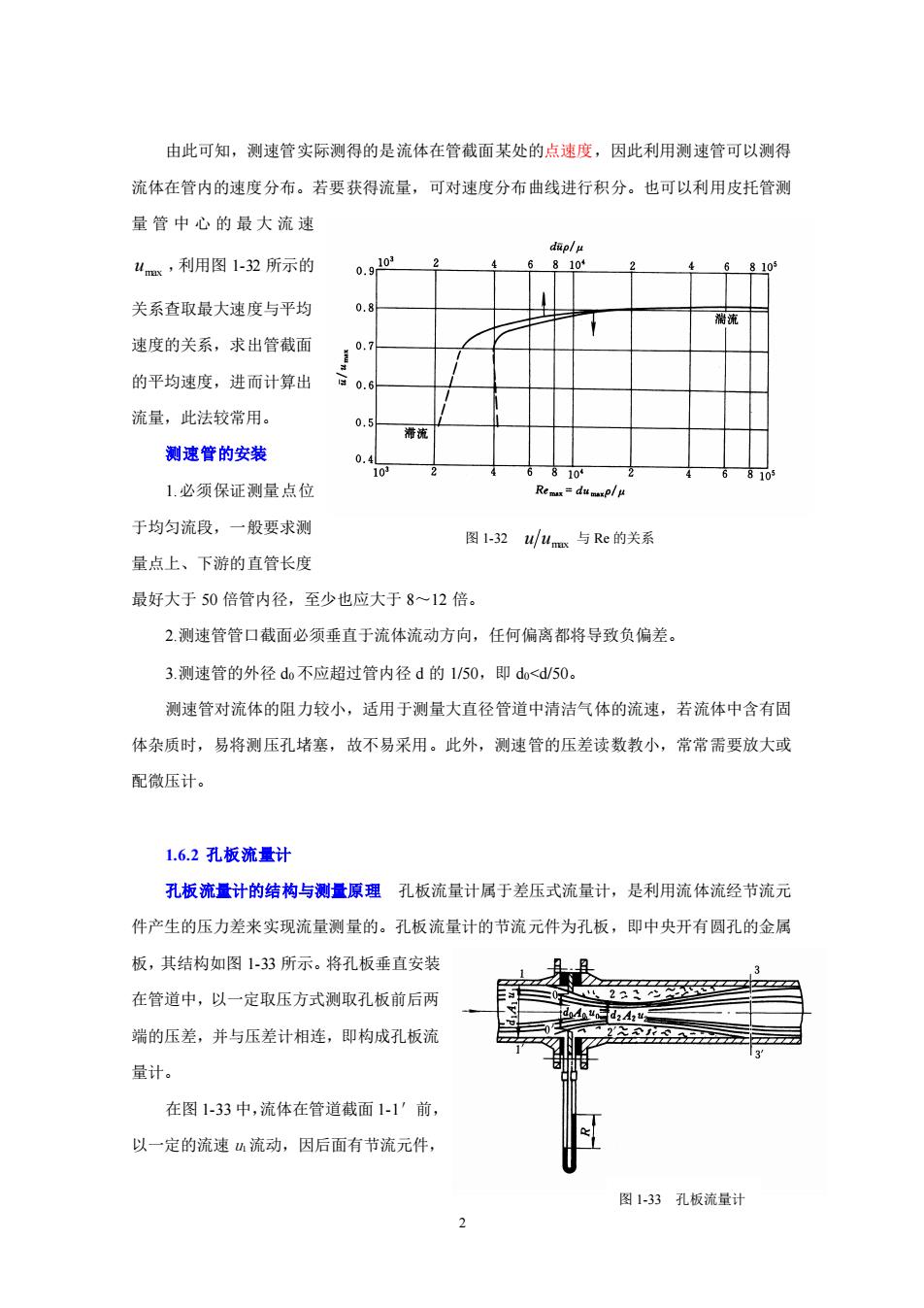
由此可知,测速管实际测得的是流体在管截面某处的点速度,因此利用测速管可以测得 流体在管内的速度分布。若要获得流量,可对速度分布曲线进行积分。也可以利用皮托管测 量管中心的最大流速 4x,利用图1-32所示的 关系查取最大速度与平均 速度的关系,求出管截面 的平均速度,进而计算出 流量,此法较常用。 测速管的安装 1.必须保证测量点位 Re 于均匀流段,一般要求测 图32 um与Re的关系 量点上、下游的直管长度 最好大于50倍管内径,至少也应大于8~12倍。 2.测速管管口截面必须垂直于流体流动方向,任何偏离都将导致负偏差。 3.测速管的外径d不应超过管内径d的1/50,即d<d50。 测速管对流体的阻力较小,适用于测量大直径管道中清洁气体的流速,若流体中含有固 体杂质时,易将测压孔堵塞,故不易采用。此外,测速管的压差读数教小,常常需要放大或 配微压计。 16.2孔板流量计 孔板流量计的结构与测量原理孔板流量计属于差压式流量计,是利用流体流经节流元 件产生的压力差来实现流量测量的。孔板流量计的节流元件为孔板,即中央开有圆孔的金属 板,其结构如图1-33所示。将孔板垂直安装 在管道中,以一定取压方式测取孔板前后两 端的压差,并与压差计相连,即构成孔板流 量计。 在图1-33中,流体在管道截面1-1’前, 以一定的流速流动,因后面有节流元件, 图1-33孔板流量计
2 由此可知,测速管实际测得的是流体在管截面某处的点速度,因此利用测速管可以测得 流体在管内的速度分布。若要获得流量,可对速度分布曲线进行积分。也可以利用皮托管测 量 管 中 心 的 最 大 流 速 max u ,利用图 1-32 所示的 关系查取最大速度与平均 速度的关系,求出管截面 的平均速度,进而计算出 流量,此法较常用。 测速管的安装 1.必须保证测量点位 于均匀流段,一般要求测 量点上、下游的直管长度 最好大于 50 倍管内径,至少也应大于 8~12 倍。 2.测速管管口截面必须垂直于流体流动方向,任何偏离都将导致负偏差。 3.测速管的外径 d0 不应超过管内径 d 的 1/50,即 d0<d/50。 测速管对流体的阻力较小,适用于测量大直径管道中清洁气体的流速,若流体中含有固 体杂质时,易将测压孔堵塞,故不易采用。此外,测速管的压差读数教小,常常需要放大或 配微压计。 1.6.2 孔板流量计 孔板流量计的结构与测量原理 孔板流量计属于差压式流量计,是利用流体流经节流元 件产生的压力差来实现流量测量的。孔板流量计的节流元件为孔板,即中央开有圆孔的金属 板,其结构如图 1-33 所示。将孔板垂直安装 在管道中,以一定取压方式测取孔板前后两 端的压差,并与压差计相连,即构成孔板流 量计。 在图 1-33 中,流体在管道截面 1-1′前, 以一定的流速 u1 流动,因后面有节流元件, 图 1-33 孔板流量计 图 1-32 u umax 与 Re 的关系

当到达截面1-1'后流束开始收缩,流速即增加。由于惯性的作用,流束的最小截面并不在孔 口处,而是经过孔板后仍继续收缩,到截面2-2'达到最小,流速,达到最大。流束截面最小 处称为缩脉。随后流束又逐渐扩大,直至截面33'处,又恢复到原有管截面,流速也降低到 原来的数值。 流体在缩脉处,流速最高,即动能最大,而相应压力就最低,因此当流体以一定流量流 经小孔时,在孔前后就产生一定的压力差△p=,一P2。流量愈大,△p也就愈大,所以利用 测量压差的方法就可以测量流量。 孔板流量计的流量方程孔板流量计的流量与压差的关系,可由连续性方程和柏努利方 程推导。 如图,在11'截面和2-2'截面间列柏努利方程,暂时不计能量损失,有 县+=会+ 变形得 G-G-卫-卫2 2 或 医陪 由于上式未考虑能量损失,实际上流体流经孔板的能量损失不能忽略不计:另外,缩脉 位置不定,山未知,但孔口面积4已知,为便于使用可用孔口速度替代缩脉处速度:同 时两测压孔的位置也不一定在1-1'和2-2'截面上,所以引入一校正系数C来校正上述各因 素的影响,则上式变为: 属-=cg (1-63) 根据连续性方程,对于不可压缩性流体得 将上式代入式(163),整理后得
3 当到达截面 1-1′后流束开始收缩,流速即增加。由于惯性的作用,流束的最小截面并不在孔 口处,而是经过孔板后仍继续收缩,到截面 2-2′达到最小,流速 u2 达到最大。流束截面最小 处称为缩脉。随后流束又逐渐扩大,直至截面 3-3′处,又恢复到原有管截面,流速也降低到 原来的数值。 流体在缩脉处,流速最高,即动能最大,而相应压力就最低,因此当流体以一定流量流 经小孔时,在孔前后就产生一定的压力差 p = p1 − p2 。流量愈大, p 也就愈大,所以利用 测量压差的方法就可以测量流量。 孔板流量计的流量方程 孔板流量计的流量与压差的关系,可由连续性方程和柏努利方 程推导。 如图,在 1-1′截面和 2-2′截面间列柏努利方程,暂时不计能量损失,有 2 2 2 2 1 1 2 1 2 1 u p u p + = + 变形得 1 2 2 1 2 2 2 u u p − p = − 或 p u u − = 2 2 1 2 2 由于上式未考虑能量损失,实际上流体流经孔板的能量损失不能忽略不计;另外,缩脉 位置不定,A2 未知,但孔口面积 A0 已知,为便于使用可用孔口速度 u0 替代缩脉处速度 u2;同 时两测压孔的位置也不一定在 1-1′和 2-2′截面上,所以引入一校正系数 C 来校正上述各因 素的影响,则上式变为: p u u C − = 2 2 1 2 0 (1-63) 根据连续性方程, 对于不可压缩性流体得 1 0 1 0 A A u = u 将上式代入式(1-63),整理后得

4= C249 (1-64) ,-(Vp A C=-c 则 wC (1-65 将U形压差计公式(1-9)代入式(1-65)中,得 2Rg(P-P】 165 根据即可计算流体的体积流量 2Rg(Po-p) 1-66 p 及质量流量 ms =CoA2Rgp(Po-p) (1-67) 式中C称为流量系数或孔流系数,其值由实 验测定。C主要取决于管道流动的雷诺数Re、孔面 积与管道面积比A/A,同时孔板的取压方式、加 工精度、管壁粗糙度等因素也对其有一定的影响。 对于取压方式、结构尺寸、加工状况均已规定的标 准孔板,流量系数C可以表示为 C.=f(Re. (1-68) 式中Re是以管道的内径d1计算的雷诺数,即 Re=dipu 23 图1-34标准孔板的流量系数 对于按标准规格及精度制作的孔板,用角接取
4 p A A C u − = 2 1 ( ) 2 1 0 0 (1-64) 令 2 1 0 0 1 ( ) A A C C − = 则 p u C = 2 0 0 (1-65) 将 U 形压差计公式(1-9)代入式(1-65)中,得 2 ( ) 0 0 0 − = Rg u C (1-65a) 根据 u0 即可计算流体的体积流量 2 ( ) 0 0 0 0 0 − = = Rg VS u A C A (1-66) 及质量流量 2 ( ) mS = C0A0 Rg 0 − (1-67) 式中 C0 称为流量系数或孔流系数,其值由实 验测定。C0 主要取决于管道流动的雷诺数 Re、孔面 积与管道面积比 A0 A1 , 同时孔板的取压方式、加 工精度、管壁粗糙度等因素也对其有一定的影响。 对于取压方式、结构尺寸、加工状况均已规定的标 准孔板,流量系数 C0 可以表示为 (Re, ) 1 0 0 A A C = f (1-68) 式中 Re 是以管道的内径 d1 计算的雷诺数,即 1 1 Re d u = 对于按标准规格及精度制作的孔板,用角接取 图 1-34 标准孔板的流量系数

压法安装在光滑管路中的标准孔板流量计,实验测得的Co与R、A,/A的关系曲线如图1-34 所示。从图中可以看出,对于A/A相同的标准孔板,C只是R的函数,并随Re的增大而 减小。当增大到一定界限值之后,C不再随R变化,成为一个仅取决于A/4的常数。选 用或设计孔板流量计时,应尽量使常用流量在此范围内。常用的C值为0.6~0.7。 用式(1-66)或(1-67)计算流体的流量时,必须先确定流量系数C0,但C。又与Re有关, 而管道中的流体流速又是未知,故无法计算Re值,此时可采用试差法。即先假设Re超过R© 界限值R,由A/A从图1-34中查得Co,然后根据式(1-66)或(1-67)计算流量,再计 算管道中的流速及相应的Re。若所得的Re值大于界限值R©c,则表明原来的假设正确,否则 需重新假设C,重复上述计算,直至计算值与假设值相符为止。 由式(1-66)可知,当流量系数C为常数时, R 或 RaVs 表明U形压差计的读数R与流量的平方成正比,即流量的少量变化将导致读数R较大 的变化,因此测量的灵敏度较高。此外,由以上关系也可以看出,孔板流量计的测量范围受U 形压差计量程的限制,同时考虑到孔板流量计的能量损失随流量的增大而迅速的增加,故孔 板流量计不适于测量流量范围较大的场合。 孔板流量计的安装与优缺点孔板流量计安装时,上、下游需要有一段内径不变的直管 作为稳定段,上游长度至少为管径的10倍,下游长度为管径的5倍。 孔板流量计结构简单,制造与安装都方便,其主要缺点是能量损失较大。这主要是由于 流体流经孔板时,截面的突然缩小与扩大形成大量涡流所致。如前所述,虽然流体经管口后 某一位置(图134中的33”截面)流速己恢复与孔板前相同,但静压力却不能恢复,产生了 永久压力降,即△p,=P,一P此压力降随面积比A/4的减小而增大。同时孔口直径减小 时,孔速提高,读数R增大,因此设计孔板流量计时应选择适当的面积比A/A以期兼顾到 U形压差计适宜的读数和允许的压力降。 例20℃苯在中133×4mm的钢管中流过,为测量苯的流量,在管道中安装一孔径为75mm 的标淮孔板流量计。当孔板前后U形压差计的读数R为80mmHg时,试求管中苯的流量(mh)
5 压法安装在光滑管路中的标准孔板流量计,实验测得的 C0 与 Re、A0 A1 的关系曲线如图 1-34 所示。从图中可以看出,对于 A0 A1 相同的标准孔板,C0 只是 Re 的函数,并随 Re 的增大而 减小。当增大到一定界限值之后,C0 不再随 Re 变化,成为一个仅取决于 A0 A1 的常数。选 用或设计孔板流量计时,应尽量使常用流量在此范围内。常用的 C0 值为 0.6~0.7。 用式(1-66)或(1-67)计算流体的流量时,必须先确定流量系数 C0,但 C0 又与 Re 有关, 而管道中的流体流速又是未知,故无法计算 Re 值,此时可采用试差法。即先假设 Re 超过 Re 界限值 ReC, 由 A0 A1 从图 1-34 中查得 C0,然后根据式(1-66)或(1-67)计算流量,再计 算管道中的流速及相应的 Re。若所得的 Re 值大于界限值 ReC, 则表明原来的假设正确,否则 需重新假设 C0,重复上述计算,直至计算值与假设值相符为止。 由式(1-66)可知,当流量系数 C0 为常数时, VS R 或 2 R VS 表明 U 形压差计的读数 R 与流量的平方成正比,即流量的少量变化将导致读数 R 较大 的变化,因此测量的灵敏度较高。此外,由以上关系也可以看出,孔板流量计的测量范围受 U 形压差计量程的限制,同时考虑到孔板流量计的能量损失随流量的增大而迅速的增加,故孔 板流量计不适于测量流量范围较大的场合。 孔板流量计的安装与优缺点 孔板流量计安装时,上、下游需要有一段内径不变的直管 作为稳定段,上游长度至少为管径的 10 倍,下游长度为管径的 5 倍。 孔板流量计结构简单,制造与安装都方便,其主要缺点是能量损失较大。这主要是由于 流体流经孔板时,截面的突然缩小与扩大形成大量涡流所致。如前所述,虽然流体经管口后 某一位置(图 1-34 中的 3-3′截面)流速已恢复与孔板前相同,但静压力却不能恢复,产生了 永久压力降,即 p f = p1 − p3 。此压力降随面积比 A0 A1 的减小而增大。同时孔口直径减小 时,孔速提高,读数 R 增大,因此设计孔板流量计时应选择适当的面积比 A0 A1 以期兼顾到 U 形压差计适宜的读数和允许的压力降。 例 20℃苯在φ133×4mm 的钢管中流过,为测量苯的流量,在管道中安装一孔径为 75mm 的标准孔板流量计。当孔板前后U形压差计的读数R 为80mmHg时,试求管中苯的流量(m3 /h)

解:查得20℃苯的物性:p=880kgm3,4=0.67×10-3Pas 面积比 设Re>Rec,由图1-34查得:C。=0.648,Rcc=1,5×103 由式(1-66),苯的体积流量: V's =CoAo 2Rg(P。-D =0.648x0.785×00752x008x981x3600-80-00136m6=48,96m7h 880 校Re:管内的流速=上- 0.0136 等407x012g1lms 管道的Re Re-4_0125×880x1l-1.81x10>Ree 0.67x10-3 故假设正确,以上计算有效。苯在管路中的流量为48.96mh。 l.6.3文丘里(Venturi)流量计 孔板流量计的主要缺点是能量损失较大,其原因在于孔板前后的突然缩小与突然扩大。若 用一段渐缩、渐扩管代替孔板,所构成的流量计称为文丘里流量计或文氏流量计,如图1-35 所示。当流体经过文丘里管 时,由于均匀收缩和逐渐扩 大,流速变化平缓,涡流较少, 故能量损失比孔板大大减少。 文丘里流量计的测量原 图1-35文丘里流量计 理与孔板流量计相同,也属于差压式流量计。其流量公式也与孔板流量计相似,即 -G4匹公-回 (1-69) 式中Cv一一文丘里流量计的流量系数(约为0.98~0.99): A0一一喉管处截面积,m2。 由于文丘里流量计的能量损失较小,其流量系数较孔板大,因此相同压差计读数R时流 6
6 解:查得 20℃苯的物性: 3 = 880kg/m , 0.67 10 Pa s 3 = − 面积比 ) 0.36 125 75 ( ) ( 2 2 1 0 1 0 = = = d d A A 设 Re Re c ,由图 1-34 查得: C0 = 0.648, 5 Re c = 1.510 由式(1-66),苯的体积流量: 0.0136m /s 48.96m /h 880 2 0.08 9.81 (13600 880) 0.648 0.785 0.075 2 ( ) 2 3 3 0 0 0 = = − = − = Rg VS C A 校核 Re: 管内的流速 1.1m/s 0.785 0.125 0.0136 4 2 2 1 = = = d V u S 管道的 Re c d u 1.81 10 Re 0.67 10 0.125 880 1.1 Re 5 3 1 = = = − 故假设正确,以上计算有效。苯在管路中的流量为 48.96m3 /h。 1.6.3 文丘里(Venturi)流量计 孔板流量计的主要缺点是能量损失较大,其原因在于孔板前后的突然缩小与突然扩大。若 用一段渐缩、渐扩管代替孔板,所构成的流量计称为文丘里流量计或文氏流量计,如图 1-35 所示。当流体经过文丘里管 时,由于均匀收缩和逐渐扩 大,流速变化平缓,涡流较少, 故能量损失比孔板大大减少。 文丘里流量计的测量原 理与孔板流量计相同,也属于差压式流量计。其流量公式也与孔板流量计相似,即 2 ( ) 0 0 − = Rg VS CV A (1-69) 式中 CV——文丘里流量计的流量系数(约为 0.98~0.99); A0——喉管处截面积,m2。 由于文丘里流量计的能量损失较小,其流量系数较孔板大,因此相同压差计读数 R 时流 图 1-35 文丘里流量计

量比孔板大。文丘里流量计的缺点是加工较难、精度要求高,因而造价高,安装时需占去一 定管长位置。 1.6.4转子流量计 转子流量计的结构与测量原理转子流量计的结构如图 1-36所示,是由一段上粗下细的锥形玻璃管(锥角约在4°左右)》 和管内一个密度大于被测流体的固体转子(或称浮子)所构成。 流体自玻璃管底部流入,经过转子和管壁之间的环隙,再从顶 部流出。 管中无流体通过时,转子沉在管底部。当被测流体以一定的 流量流经转子与管壁之间的环隙时,由于流道截面减小,流速 增大,压力随之降低,于是在转子上、下端面形成一个压差 将转子托起,使转子上浮。随转子的上浮,环隙面积逐渐增大, 流体入口 流速减小,压力增加,从而使转子两端的压差降低。当转子上 浮至某一定高度时,转子两端面压差造成的升力恰好等于转子 图1-36转子流量计 1一锥形硬玻璃管:2一一刻度 的重力时,转子不再上升,而悬浮在该高度。转子流量计玻璃 3一一突缘填函盖板:4一转子 管外表面上刻有流量值,根据转子平衡时其上端平面所处的位置,即可读取相应的流量。 转子流量计的流量方程转子流量计的流量方程可根据转子受 力平衡导出。 在图1-37中,取转子下端截面为1-1'上端藏面为00',用 PA,P,分别表示转子的体积、最大截面积和密度。当转子处 于平衡位置时,转子两端面压差造成的升力等于转子的重力,即 (P-Po)Ar=P V1g (1-70) 图137转子流量计流动示意图 P、P的关系可在1'和0-0'截面间列柏努利方程获得: 合+号+g=合+号+8 整理得 p-%=(eo-)pg+号(u-4) 将上式两端同乘以转子最大截面积4,则有
7 量比孔板大。文丘里流量计的缺点是加工较难、精度要求高,因而造价高,安装时需占去一 定管长位置。 1.6.4 转子流量计 转子流量计的结构与测量原理 转子流量计的结构如图 1-36 所示,是由一段上粗下细的锥形玻璃管(锥角约在 4°左右) 和管内一个密度大于被测流体的固体转子(或称浮子)所构成。 流体自玻璃管底部流入,经过转子和管壁之间的环隙,再从顶 部流出。 管中无流体通过时,转子沉在管底部。当被测流体以一定的 流量流经转子与管壁之间的环隙时,由于流道截面减小,流速 增大,压力随之降低,于是在转子上、下端面形成一个压差, 将转子托起,使转子上浮。随转子的上浮,环隙面积逐渐增大, 流速减小,压力增加,从而使转子两端的压差降低。当转子上 浮至某一定高度时,转子两端面压差造成的升力恰好等于转子 的重力时,转子不再上升,而悬浮在该高度。转子流量计玻璃 管外表面上刻有流量值,根据转子平衡时其上端平面所处的位置,即可读取相应的流量。 转子流量计的流量方程 转子流量计的流量方程可根据转子受 力平衡导出。 在图 1-37 中,取转子下端截面为 1-1′上端截面为 0-0′,用 Vf、Af、 f 分别表示转子的体积、最大截面积和密度。当转子处 于平衡位置时,转子两端面压差造成的升力等于转子的重力,即 ( p1 − p0 )Af = fVf g (1-70) 1 p 、 0 p 的关系可在 1-1′和 0-0′截面间列柏努利方程获得: z g p u z g p u 0 2 0 0 1 2 1 1 2 2 + + = + + 整理得 ( ) 2 ( ) 2 1 2 p1 − p0 = z0 − z1 g + u0 − u 将上式两端同乘以转子最大截面积 Af,则有 图 1-36 转子流量计 1——锥形硬玻璃管;2——刻度; 3——突缘填函盖板;4——转子 图 1-37 转子流量计流动示意图 u 0 0′ 1′ 0 1

(p1-Pa)4y=A(30-)pg+A号(6-) (1-71) 由此可见,流体作用于转子的升力(P,一P)4,由两部分组成:一部分是两截面的位差。 此部分作用于转子的力即为流体的浮力,其大小为A,(仁。一)P8即',Pg:另一部分是两截 面的动能差,其值为4,号(-). 将式(1-70)与(1-71)联立,得 y(p,-pg=A,号G-ui (1-72) 根据连续性方程 4 将上式代入式(12)中,有 o,-pg=4,G1-( 1 整理得 2V(P1-P)8 4= (1-73) PA 考虑到表面摩擦和转子形状的影响,引入校正系数C,则有 2(P:-P)V18 (1-74) 此式即为流体流过环隙时的速度计算式,C又称为转子流量计的流量系数。 转子流量计的体积流量为 2Pr-pΨr8 (1-75) 式中A奴为转子上端面处环隙面积。 转子流量计的流量系数CR与转子的形状和流体流过环隙时的R有关。对于一定形状的 转子,当Re达到一定数值后,CR为常数。 由式(1-74)可知,对于一定的转子和被测流体,'Ar Pr p为常数,当Re较大 时,C也为常数,故。为一定值,即无论转子停在任何一个位置,其环隙流速山。是恒定的
8 ( ) 2 ( ) ( ) 2 1 2 p1 − p0 Af = Af z0 − z1 g + Af u0 − u (1-71) 由此可见,流体作用于转子的升力 p p Af ( ) 1 − 0 由两部分组成:一部分是两截面的位差, 此部分作用于转子的力即为流体的浮力,其大小为 Af (z0 − z1 )g 即 Vf g ;另一部分是两截 面的动能差,其值为 ( ) 2 2 1 2 Af u0 − u 。 将式(1-70)与(1-71)联立,得 ( ) 2 ( ) 2 1 2 Vf f − g = Af u0 − u (1-72) 根据连续性方程 1 0 1 0 A A u = u 将上式代入式(1-72)中,有 − = − 2 1 2 0 0 1 ( ) 2 ( ) A A Vf f g Af u 整理得 f f f A V g A A u 2 ( ) 1 1 2 1 0 0 − − = (1-73) 考虑到表面摩擦和转子形状的影响,引入校正系数 CR,则有 f f f R A V g u C 2( ) 0 − = (1-74) 此式即为流体流过环隙时的速度计算式,CR又称为转子流量计的流量系数。 转子流量计的体积流量为 f f f R R A V g Vs C A 2( − ) = (1-75) 式中 AR为转子上端面处环隙面积。 转子流量计的流量系数 CR 与转子的形状和流体流过环隙时的 Re 有关。对于一定形状的 转子,当 Re 达到一定数值后,CR为常数。 由式(1-74)可知,对于一定的转子和被测流体, Vf、Af、 f、 为常数,当 Re 较大 时,CR也为常数,故 0 u 为一定值,即无论转子停在任何一个位置,其环隙流速 0 u 是恒定的

而流量与环隙面积成正比即VA®,由于玻璃管为下小上大的锥体,当转子停留在不同高 度时,环隙面积不同,因而流量不同。 当流量变化时,力平衡关系式(10)并未改变,也即转子上、下两端面的压差为常数。 所以转子流量计的特点为恒压差、恒环隙流速而变流通面积,属于截面式流量计。与之相反 孔板流量计则是恒流通面积,而压差随流量变化,为差压式流量计。 转子流量计的刻度换算转子流量计上的刻度,是在出厂前用某种流体进行标定的。一 般液体流量计用20℃的水(密度为1000kgm3)标定,而气体流量计则用20℃和101.3kPa下 的空气(密度为12kgm3)标定。当被测流体与上述条件不符时,应进行刻度换算 假定Ck相同,在同一刻度下,有 =- (1-76) Vs VP:(er-A) 式中下标1表示标定流体的参数,下标2表示实际被测流体 的参数。 对于气体转子流量计,因转子材料的密度远大于气体密度, 式(1-76)可简化为 (1-76a 转子流量计必须垂直安装在管路上,为便于检修,应设置如 图1-38所示的支路。 转子流量计读数方便,流动阻力很小,测量范围宽,测量精 图1-38转子流量计安装示意图 度较高,对不同的流体适用性广。缺点是玻璃管不能经受高温和 高压,在安装使用过程中玻璃容易破碎。 例某气体转子流量计的量程范围为4~60mh。现用来测量压力为60Pa(表压)、温度 为50℃的氨气,转子流量计的读数应如何校正?此时流量量程的范围又为多少?(设流量系 数CR为常数,当地大气压为1013kPa) 解:操作条件下氨气的密度: A-2-013+60007-=1022em RT 8.31×(273+50)
9 而流量与环隙面积成正比即 VS AR ,由于玻璃管为下小上大的锥体,当转子停留在不同高 度时,环隙面积不同,因而流量不同。 当流量变化时,力平衡关系式(1-70)并未改变,也即转子上、下两端面的压差为常数, 所以转子流量计的特点为恒压差、恒环隙流速而变流通面积,属于截面式流量计。与之相反, 孔板流量计则是恒流通面积,而压差随流量变化,为差压式流量计。 转子流量计的刻度换算 转子流量计上的刻度,是在出厂前用某种流体进行标定的。一 般液体流量计用 20℃的水(密度为 1000kg/m3)标定,而气体流量计则用 20℃和 101.3kPa 下 的空气(密度为 1.2kg/m3)标定。当被测流体与上述条件不符时,应进行刻度换算。 假定 CR相同,在同一刻度下,有 ( ) ( ) 2 1 1 2 1 2 − − = f f S S V V (1-76 ) 式中下标 1 表示标定流体的参数,下标 2 表示实际被测流体 的参数。 对于气体转子流量计,因转子材料的密度远大于气体密度, 式(1-76)可简化为 2 1 1 2 S S V V (1-76a) 转子流量计必须垂直安装在管路上,为便于检修,应设置如 图 1-38 所示的支路。 转子流量计读数方便,流动阻力很小,测量范围宽,测量精 度较高,对不同的流体适用性广。缺点是玻璃管不能经受高温和 高压,在安装使用过程中玻璃容易破碎。 例 某气体转子流量计的量程范围为 4~60m3 /h。现用来测量压力为 60kPa(表压)、温度 为 50℃的氨气,转子流量计的读数应如何校正?此时流量量程的范围又为多少?(设流量系 数 CR为常数,当地大气压为 101.3 kPa) 解:操作条件下氨气的密度: 3 3 2 1.022kg/m 8.31 (273 50) (101.3 60) 10 0.017 = + + = = RT pM 图 1-38 转子流量计安装示意图

即同一刻度下,氨气的流量应是空气流量的1.084倍。 此时转子流量计的流量范围为4×1.084~60×1.084m3h,即4.34~65.0m3h
10 1.084 1.022 1.2 2 1 1 2 = = S S V V 即同一刻度下,氨气的流量应是空气流量的 1.084 倍。 此时转子流量计的流量范围为 4×1.084~60×1.084m3 /h,即 4.34~65.0 m3 /h