
第三章机械分离 非均相混合物的特点是体系内包含一个以上的相,相界面两侧物质的性质完全不同,如 由固体颗粒与液体构成的悬浮液、由周体颗粒与气体构成的含尘气体等。这类混合物的分离 就是将不同的相分开,通常采用机械的方法。 第一节颗粒沉降 本节讨论如何利用颗粒沉降运动来分离非均相混合物,为此首先要认识沉降运动现象。 一固体颗粒在流体中的沉降运动现象 1.颗粒沉降运动中的受力分析 (1)当固体处于流体中时,只要两者的密度有差异,则在重力场中颗粒将在重力方向 与流体作相对运动:在离心力场中与流体在离心力方向上作相对运动。 直径为d的球形颗粒受到的重力为:名。,8:其中。,为颗粒密度。 直径为d的球形颗粒受到的离心力为:dp,a-d,:其方向是从圆心指向外。 (2)颗粒处于流体中,无论运动与否,都会受到浮力。 当流体处于重力场中,颗粒受到的浮力等于:二户8: 流体在离心力场中时,颗粒也要受到一个类似于重力场中浮力的力:二d'二 (3)分析颗粒沉降运动必须考虑流体对颗粒运动的阻力。 (4)两种阻力:包括表皮阻力和形体阻力。当颗粒速度很小时,流体对球的运动阻力 主要是粘性摩擦或表皮阻力。若速度增加,便有旋涡出现,即发生边界层分离,表皮阻力让 位于形体阻力。 阻力大小的计算仿照管路阻力的计算,即认为阻力与相对运动速度的平方成正比。对于 直径为山的球形颗粒:( 2.沉降速度与阻力系数 (1)重力沉度: 重力场中,颗粒在流体中受到重力、浮力和阻力,这些力会使颗粒产生一个加速度,根 据牛顿第二定律:重力-浮力-阻力=颗粒质量×加速度。当颗粒在流体中做均速运动时, 事实上,颗粒从静止开始作沉降运动时,分为加速和均速两个阶段。速度越大阻力越大, 加速度越小零;加速度为零时颗粒便作均速运动,其速度称为沉降速度。一般而言,对小颗 粒,加速阶段时间很短,通常忽略,可以认为沉降过程是均速的。令颗粒所受合力为零,便 可解出沉降速度:
第三章 机械分离 非均相混合物的特点是体系内包含一个以上的相,相界面两侧物质的性质完全不同,如 由固体颗粒与液体构成的悬浮液、由固体颗粒与气体构成的含尘气体等。这类混合物的分离 就是将不同的相分开,通常采用机械的方法。 第一节 颗粒沉降 本节讨论如何利用颗粒沉降运动来分离非均相混合物,为此首先要认识沉降运动现象。 一 固体颗粒在流体中的沉降运动现象 1.颗粒沉降运动中的受力分析 (1)当固体处于流体中时,只要两者的密度有差异,则在重力场中颗粒将在重力方向 与流体作相对运动;在离心力场中与流体在离心力方向上作相对运动。 直径为 d 的球形颗粒受到的重力为: d s g 3 6 ;其中 s 为颗粒密度。 直径为 d 的球形颗粒受到的离心力为: r u d a d t s r s 2 3 3 6 6 = ;其方向是从圆心指向外。 (2)颗粒处于流体中,无论运动与否,都会受到浮力。 当流体处于重力场中,颗粒受到的浮力等于: d g 3 6 ; 流体在离心力场中时,颗粒也要受到一个类似于重力场中浮力的力: r u d t 2 3 6 (3)分析颗粒沉降运动必须考虑流体对颗粒运动的阻力。 (4)两种阻力:包括表皮阻力和形体阻力。当颗粒速度很小时,流体对球的运动阻力 主要是粘性摩擦或表皮阻力。若速度增加,便有旋涡出现,即发生边界层分离,表皮阻力让 位于形体阻力。 阻力大小的计算仿照管路阻力的计算,即认为阻力与相对运动速度的平方成正比。对于 直径为 d 的球形颗粒: 2 4 2 2 u0 d 2.沉降速度与阻力系数 (1)重力沉降速度: 重力场中,颗粒在流体中受到重力、浮力和阻力,这些力会使颗粒产生一个加速度,根 据牛顿第二定律:重力-浮力-阻力=颗粒质量×加速度。当颗粒在流体中做均速运动时, d s g 3 6 - d g 3 6 - 2 4 2 2 u0 d =0 事实上,颗粒从静止开始作沉降运动时,分为加速和均速两个阶段。速度越大阻力越大, 加速度越小零;加速度为零时颗粒便作均速运动,其速度称为沉降速度。一般而言,对小颗 粒,加速阶段时间很短,通常忽略,可以认为沉降过程是均速的。令颗粒所受合力为零,便 可解出沉降速度:
解得 wo-iato.-ok (1) 3p (2)离心沉牌速度 按照与上面相同的方法,可以得到离心沉降速度的表示式,它在形式上与重力沉降速度 表达式一样,只是将重力加速度代之以离心加速度: 4,= 4d(p,-phui (2) 3pg 注意:颗粒离心沉降的速度方向是则圆心指向外周,但由于颗粒和流体同时做圆周运动,颗 粒的实际运动轨迹是一个半径逐渐扩大的螺旋线。离心沉降速度并不是颗粒的实际运动速 度,只是其在径向上的分量 (3)其它图素对沉降速度的影陶:上述计算沉降速度的方法,是在下列条件下建立的: ①颗粒为球形:②颗粒沉降时彼此相距较远,互不干扰:③容器壁对沉降的阻滞作用可以忽 略:④颗粒直径不能小到受流体分子运动的影响, 在一定条件下,上述各种因素都可能会对沉降过程产生影响,详情参见教材。 (4)越力票熟:使用式(】)或(2)计算沉降速度首先要知道阻力系数,通过因次分 析法可知它是颗粒与流体相对运动雷诺数的函数:5=feo面Re。-血P。计算Re。时 d应为足以表征颗粒大小的长度,对球形颗粒而言,自然是它的直径。 球形颗粒沉降的阻力系数 R.-du/u 1000001000010030000000 根据实验结果作出的阻力系数与雷诺的关系如图所示,其变化规律可以分成四段,用不 同的公式表示。第一段的表达式是准确的,其它几段是近似的。 ①层流区—e<03—5- 24 一w=4产DgDS,可以近似用到e,=2. 一—Stokes定律,沉降操作中所涉及的颗粒一般都很小,R。通常在0.3以内,故该式很 常用
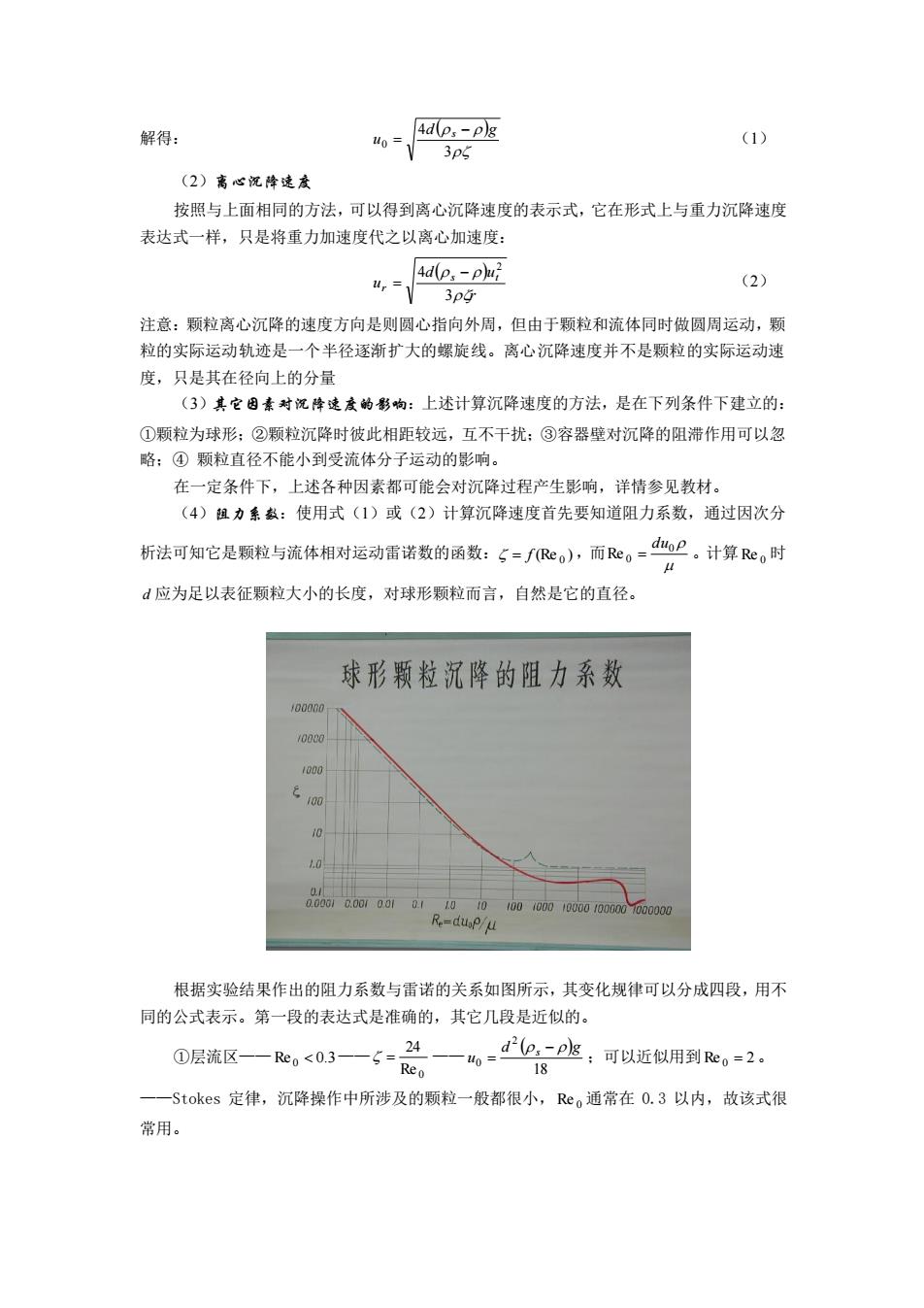
解得: ( ) 3 4 0 d g u s − = (1) (2)离心沉降速度 按照与上面相同的方法,可以得到离心沉降速度的表示式,它在形式上与重力沉降速度 表达式一样,只是将重力加速度代之以离心加速度: ( ) r d u u s t r 3 4 2 − = (2) 注意:颗粒离心沉降的速度方向是则圆心指向外周,但由于颗粒和流体同时做圆周运动,颗 粒的实际运动轨迹是一个半径逐渐扩大的螺旋线。离心沉降速度并不是颗粒的实际运动速 度,只是其在径向上的分量 (3)其它因素对沉降速度的影响:上述计算沉降速度的方法,是在下列条件下建立的: ①颗粒为球形;②颗粒沉降时彼此相距较远,互不干扰;③容器壁对沉降的阻滞作用可以忽 略;④ 颗粒直径不能小到受流体分子运动的影响。 在一定条件下,上述各种因素都可能会对沉降过程产生影响,详情参见教材。 (4)阻力系数:使用式(1)或(2)计算沉降速度首先要知道阻力系数,通过因次分 析法可知它是颗粒与流体相对运动雷诺数的函数: (Re ) 0 = f ,而 0 Re 0 du = 。计算 Re 0 时 d 应为足以表征颗粒大小的长度,对球形颗粒而言,自然是它的直径。 根据实验结果作出的阻力系数与雷诺的关系如图所示,其变化规律可以分成四段,用不 同的公式表示。第一段的表达式是准确的,其它几段是近似的。 ①层流区—— Re 0 0.3—— Re 0 24 = —— ( ) 18 2 0 d g u s − = ;可以近似用到 Re 0 = 2。 ——Stokes 定律,沉降操作中所涉及的颗粒一般都很小, Re 0 通常在 0.3 以内,故该式很 常用

②驱m区)一2,0一器一-0o空 腊流区(牛预K)一02x103后,5骤然下降,在Reo=(3-10)×103范围内可近似取5=0.1. (5)公式使用方法 ①如果事前能够上确认沉降动处在哪个区,则直接就用该区的公式进行计算。 ②如果不能确定流动处在哪个区,则应采用试法:即先假定流动处于层流区,用Stokes 公式求出沉降速度,然后再计算雷诺数Reo:如果Reo>2,便改用相应的公式计算o, 新算出的,也要检验,直到确认所用的公式正确为止。 ③通过实验整理数据得到: Re0-18+06m Ar (3) 其中r称为啊基米德准数,_2-p兆。计算时先根据已知条件计算,然后由式 (3)计算Reo,最后根据Reo反算出沉降速度 ④上述公式,若将重力加速度改为离心加速度,则都可用于离心力场中沉降速度的计算。 二重力沉降分离设备 1.分级器 利用不同粒径或不同密度的颗粒在流体中的沉降速度不同这一原理来实现它们分离的 设备称为分级器 将沉降速度不同的两种颗粒倾倒到向上流动的水流中,若水的速度调整到在两者的沉降 速度之间,则沉降速度较小的那部分颗粒便被漂走分出。若有密度不同的a、b两种颗粒要 分离,且两种颗粒的直径范围都很大,则由于密度大而直径小的颗粒与密度小而直径大的颗 粒可能具有相同的沉降速度,使两者不能完全分离。 dp。-pg_dps-pk 18u 184 上式表明,不同直径的颗粒因为密度不同而具有相同的沉降速度,该式代表了具有相同沉降 速度的两种颗粒的直径比。 俐数】石英和方铅矿的混合球形颗粒在如图所示的水力分级器中进行分离。两者的密度分 别为2650kg/m3和7500kg/m,且粒度范围均为20~100m。水温为20℃。假设颗粒在分级 器中均作自由沉降,试计算能够得到纯石英和纯方铅矿的粒度范围及三个分级器中的水流速 度
②过渡区(Allen 区)——2 Re 0 500 —— 0.6 Re 0 18.5 = —— ( ) 0.6 0 0 Re 0.269 − = gd s u ③湍流区(牛顿区)——500 Re 0 200000 —— = 0.44—— ( ) − = gd s u0 1.74 ④ 5 Re0 210 后, 骤然下降,在 5 Re0 = (3 ~10)10 范围内可近似取 = 0.1。 (5)公式使用方法 ①如果事前能够上确认沉降动处在哪个区,则直接就用该区的公式进行计算。 ②如果不能确定流动处在哪个区,则应采用试法:即先假定流动处于层流区,用 Stokes 公式求出沉降速度 u0 ,然后再计算雷诺数 Re 0 ;如果 Re 0 2 ,便改用相应的公式计算 u0 , 新算出的 u0 也要检验,直到确认所用的公式正确为止。 ③通过实验整理数据得到: Ar Ar 18 0.6 Re 0 + = (3) 其中 Ar 称为阿基米德准数, ( ) 2 3 d g Ar s − = 。计算时先根据已知条件计算 Ar ,然后由式 (3)计算 Re 0 ,最后根据 Re 0 反算出沉降速度 u0 ④上述公式,若将重力加速度改为离心加速度,则都可用于离心力场中沉降速度的计算。 二 重力沉降分离设备 1.分级器 利用不同粒径或不同密度的颗粒在流体中的沉降速度不同这一原理来实现它们分离的 设备称为分级器。 将沉降速度不同的两种颗粒倾倒到向上流动的水流中,若水的速度调整到在两者的沉降 速度之间,则沉降速度较小的那部分颗粒便被漂走分出。若有密度不同的 a、b 两种颗粒要 分离,且两种颗粒的直径范围都很大,则由于密度大而直径小的颗粒与密度小而直径大的颗 粒可能具有相同的沉降速度,使两者不能完全分离。 ( ) ( ) 18 18 2 2 da a g db b − g = − 1/ 2 − − = b a a b d d 上式表明,不同直径的颗粒因为密度不同而具有相同的沉降速度,该式代表了具有相同沉降 速度的两种颗粒的直径比。 例题 1 石英和方铅矿的混合球形颗粒在如图所示的水力分级器中进行分离。两者的密度分 别为 2650kg/m3 和 7500kg/m3,且粒度范围均为 20 ~100m 。水温为 20℃。假设颗粒在分级 器中均作自由沉降。试计算能够得到纯石英和纯方铅矿的粒度范围及三个分级器中的水流速 度
固体混合物 澄清液 水 自 解:(缺扫描图) 1、2、3号分级器直径逐渐增大而三者中上升水流量均相同,所以水在三者中流速逐渐 减小。水在1号中的速度最大,可将密度小的石英颗粒全部带走,于是1号底部可得到纯方 铅矿。但是,也有部分小颗粒的方铅矿随同全部石英被带走。在2号分级器,控制水流速度 将全部方铅可全部沉降下米,但也有部分大颗粒石英会沉降下米。在3号分级器,控制水流 速度,可将全部小石英粒子全部沉降下来。 综上所述,1号分级器的作用在于要带走大所有石英粒子(最大为100m),因此1号 的水流速应该等于100m石英的沉降速度:2号的作用在于截下全部方铅矿(最小为 20m),因此2号的水流速应该等于20m方铅矿的沉降速度:3号的作用在于截下全部石 英粒子(最小为20m),因此3号水流速应该等204m石英的沉降速度。 1号分级器中的水流速:4=。二pk_0x100-82水981三%×10m, 180 18×1.005×10- 校核:Re1-恤卫_1@×10x86x10x9%2-09,近似认为处于层流区。 18×1.005×10- 在19发发分支省小学-胎 人m紧” =50.4m(该值也可由水流速度反算) 所以,在1号分级器中得到纯方铅矿的粒度范围为:50.4~100m 2号分级器中的水流速:4-4心g-p兆.x100-982k91-141×10m1: 18 18×1.005×10 在该速度下能被在2号中被沉降下来的最小石英粒子: d.-e-) 因此,在2号中,方铅矿20~50.4m:石英39.7~100m
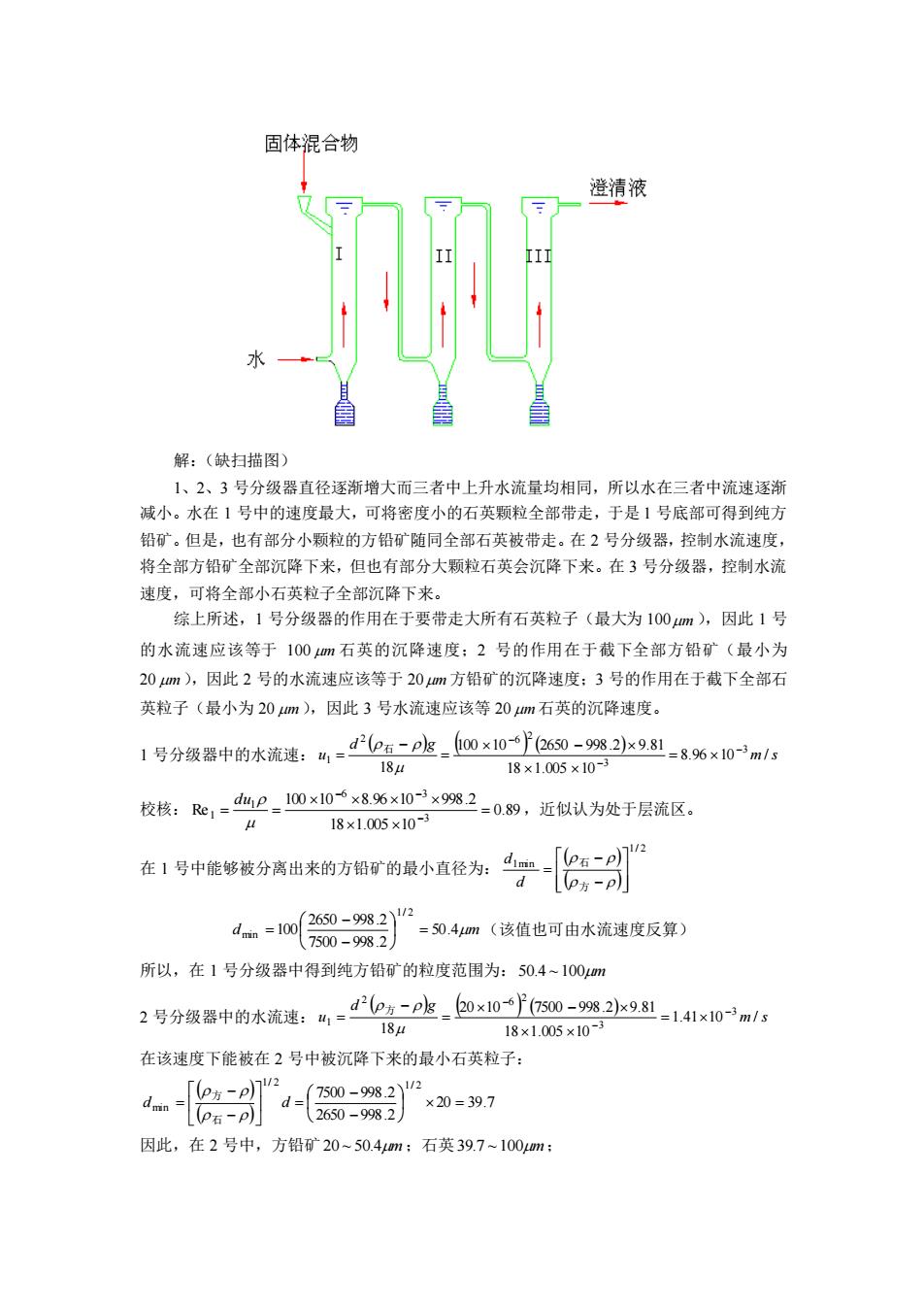
解:(缺扫描图) 1、2、3 号分级器直径逐渐增大而三者中上升水流量均相同,所以水在三者中流速逐渐 减小。水在 1 号中的速度最大,可将密度小的石英颗粒全部带走,于是 1 号底部可得到纯方 铅矿。但是,也有部分小颗粒的方铅矿随同全部石英被带走。在 2 号分级器,控制水流速度, 将全部方铅矿全部沉降下来,但也有部分大颗粒石英会沉降下来。在 3 号分级器,控制水流 速度,可将全部小石英粒子全部沉降下来。 综上所述,1 号分级器的作用在于要带走大所有石英粒子(最大为 100 m ),因此 1 号 的水流速应该等于 100 m 石英的沉降速度;2 号的作用在于截下全部方铅矿(最小为 20 m ),因此 2 号的水流速应该等于 20 m 方铅矿的沉降速度;3 号的作用在于截下全部石 英粒子(最小为 20 m ),因此 3 号水流速应该等 20 m 石英的沉降速度。 1 号分级器中的水流速: ( ) ( ) ( ) m s d g u 8.96 10 / 18 1.005 10 100 10 2650 998.2 9.81 18 3 3 2 2 6 1 − − − = − = − = 石 校核: 0.89 18 1.005 10 100 10 8.96 10 998.2 Re 3 6 3 1 1 = = = − − − du ,近似认为处于层流区。 在 1 号中能够被分离出来的方铅矿的最小直径为: ( ) ( ) 1/ 2 1min − − = 方 石 d d d 50.4m 7500 998.2 2650 998.2 100 1/ 2 min = − − = (该值也可由水流速度反算) 所以,在 1 号分级器中得到纯方铅矿的粒度范围为: 50.4 ~100m 2 号分级器中的水流速: ( ) ( ) ( ) m s d g u 1.41 10 / 18 1.005 10 20 10 7500 998.2 9.81 18 3 3 2 2 6 1 − − − = − = − = 方 在该速度下能被在 2 号中被沉降下来的最小石英粒子: ( ) ( ) 20 39.7 2650 998.2 7500 998.2 1/ 2 1/ 2 min = − − = − − d = d 石 方 因此,在 2 号中,方铅矿 20 ~ 50.4m ;石英 39.7 ~100m ;

18×1.005×10 在3号中能被截下的是20-397m的石英。 2.降尘室 在电室中的动 (1)工作原理: 如图所示,气体入室后,因流通截面扩大而速度减慢。气流中的尘粒一方面随气流沿水 平方向运动,其速度与气流速度,相同:另一方面在重力作用下以沉降速度垂直向下运 动。只要气体室内所经历时间大于尘粒从室顶沉降到室底所用时间,尘粒便可分离出来。 (2)装被除去的最小颗粒直径:显然,粒子直径越大,越容易被除去。下面考虑如何 确定能被作夫的最小题粒直径。前已述及,某一粒径的粒子能100%被除去的条件是其从室 项沉降到室底所需要时间小于气流在室内的停留时间,前者可用该粒子的室高除以沉降速度 而得:而后者由室长除以气流速度而得: (4) 其中为以气体体积流量表示的处理量,ms:4为降尘室的底面积,m。该式给出了颗 粒能被除去的条件,即其沉降速度要大于处理量与底面积之商。显然,该式取等号式时对应 着能被除去的最小颗粒(因为考虑的是最小颗粒直径,所以可以认为沉降运动处于层流区)。 =8d,-p).y 18u V. ,dmn=gp,-p4 (5) 184 镜明:显然,能被(100%)除去的最小颗粒尺寸不仅与颗粒和气体的性质有关,还与处理 量和降尘室底面积有关。 (3)最大处理量: 由式(4)可知,,≤6,由此可以计算含尘气体 的最大处理量 说明①含尘气体的最大处理量与某一粒径对应的,是指这 粒径及大于该粒径的颗粒都能100%被除去时的最大气体 童 ②最大的气体处理量不仅与粒径相对应,还与降尘室 底面积有关,底面积越大处理量裁大,但处理量与高度无 关。为此,降尘室都做成扁平形:为提高气体处理量,室 内以水平隔板将降尘室分割居若干层,称为多层降尘室。 隔板的间距应考虑出灰的方便 (4)补充说明:①气体在峰尘室内流通截面上的均布
( ) ( ) ( ) m s d g u 3.583 10 / 18 1.005 10 20 10 2650 998.2 9.81 18 3 3 2 2 6 3 − − − = − = − = 石 在 3 号中能被截下的是 20 ~ 39.7m 的石英。 2.降尘室 (1)工作原理: 如图所示,气体入室后,因流通截面扩大而速度减慢。气流中的尘粒一方面随气流沿水 平方向运动,其速度与气流速度 u 相同;另一方面在重力作用下以沉降速度 u0 垂直向下运 动。只要气体室内所经历时间大于尘粒从室顶沉降到室底所用时间,尘粒便可分离出来。 (2)能被除去的最小颗粒直径:显然,粒子直径越大,越容易被除去。下面考虑如何 确定能被作去的最小颗粒直径。前已述及,某一粒径的粒子能 100%被除去的条件是其从室 顶沉降到室底所需要时间小于气流在室内的停留时间,前者可用该粒子的室高除以沉降速度 而得;而后者由室长除以气流速度而得: u L u H 0 ,即 0 0 A V LB HBu L Hu u s = = (4) 其中 Vs 为以气体体积流量表示的处理量,m3 /s; A0 为降尘室的底面积,㎡。该式给出了颗 粒能被除去的条件,即其沉降速度要大于处理量与底面积之商。显然,该式取等号式时对应 着能被除去的最小颗粒(因为考虑的是最小颗粒直径,所以可以认为沉降运动处于层流区)。 ( ) 0 2 min 0 18 A gd V u s s = − = , ( ) 0 min 18 A V g d s s − = (5) 说明:显然,能被(100%)除去的最小颗粒尺寸不仅与颗粒和气体的性质有关,还与处理 量和降尘室底面积有关。 (3)最大处理量: 由式(4)可知, Vs A0u0 ,由此可以计算含尘气体 的最大处理量。 说明①含尘气体的最大处理量与某一粒径对应的,是指这 一粒径及大于该粒径的颗粒都能 100%被除去时的最大气体 量; ②最大的气体处理量不仅与粒径相对应,还与降尘室 底面积有关,底面积越大处理量越大,但处理量与高度无 关。为此,降尘室都做成扁平形;为提高气体处理量,室 内以水平隔板将降尘室分割居若干层,称为多层降尘室。 隔板的间距应考虑出灰的方便。 (4)补充说明:①气体在降尘室内流通截面上的均布

非常重要,分布不均必须有部分气体在室内停留时间过短,其中所含颗粒来不及沉降而被带 出室外。为使气体均布,降尘室进出口通常都做成锥形:②为防止操作过程中已被除下的尘 粒又被气流重新卷起,降尘室的操作气速往往很低:另外,为保证分离效率,室底面积也必 须较大。因此,降尘室是一种庞大而低效的设备,通常只能捕获大于50m的粗题粒。要将 更细小的颗粒分离出米,就必须采用更高效的除尘设备。 3.沉降槽 三离心沉降设备 颗粒在重力或离心力场中都可发生沉降过程。利用离心力比利用重力要有效得多,因为 颗粒的离心力由旋转而产生,转速越大,则离心力越大:而颗粒所受的重力却是固定的。因 此,利用离心力作用的分离设备不仅可以分离出比较小的颗粒,而且设备的体积也可缩小很 多。 1.旋风分离器 (1)构造与工作原理:旋风分离器是利用离心沉降原理从气流中分离出颗粒的设备。 如图所示,上部为圆筒形、下部为圆锥形:含尘气体从圆筒上侧的矩形进气管以切线方向进 入,霜此来获得器内的旋转运动。气体在器内按螺旋形路线向器底旋转,到达底部后折而向 上,成为内层的上旋的气流,称为气芯,然后从项部的中央排气管挂出。气体中所夹带的尘 粒在随气流旋转的过程中,由于密度较大,受离心力的作用逐渐沉降到器壁,碰到器壁后落 下,滑向出灰口。 旋风分离器各部分的尺寸都有一定的比例,只要规定出其中一个主要尺寸,如圆筒直径 D或进气口宽度B,则其它各部分的尺寸亦确定。 (2)分离性能信什 ①能被分离出的最小颗粒直径一一临界直径d: 假定:颗粒与气体在旋风分离器内的切线速度,恒定,与所在位置无关,且等于在进 口处的速度山,:颗粒沉降过程中所穿过的最大气层厚度等进气口宽度B:颗粒与气流的相对 运动为层流。 速度山,旋转半径取平均值,则沉降速度可表示为: d-o.uz ,二18 根据第二条假设, 沉降时间=B=18:B d2p, 令气体进入气芯以前在向内旋转的圈数为N,由运行距离为2mN,故得气体在器内的 有效停留时间为: 停留时间:2 某一粒径的颗粒能100%地被分离出来的条件是:该粒径的颗粒穿过最大气层厚度所需 要时间小于等于气体在器内的有效停留时间,即
非常重要,分布不均必须有部分气体在室内停留时间过短,其中所含颗粒来不及沉降而被带 出室外。为使气体均布,降尘室进出口通常都做成锥形;②为防止操作过程中已被除下的尘 粒又被气流重新卷起,降尘室的操作气速往往很低;另外,为保证分离效率,室底面积也必 须较大。因此,降尘室是一种庞大而低效的设备,通常只能捕获大于 50 m 的粗颗粒。要将 更细小的颗粒分离出来,就必须采用更高效的除尘设备。 3.沉降槽 三 离心沉降设备 颗粒在重力或离心力场中都可发生沉降过程。利用离心力比利用重力要有效得多,因为 颗粒的离心力由旋转而产生,转速越大,则离心力越大;而颗粒所受的重力却是固定的。因 此,利用离心力作用的分离设备不仅可以分离出比较小的颗粒,而且设备的体积也可缩小很 多。 1.旋风分离器 (1)构造与工作原理:旋风分离器是利用离心沉降原理从气流中分离出颗粒的设备。 如图所示,上部为圆筒形、下部为圆锥形;含尘气体从圆筒上侧的矩形进气管以切线方向进 入,藉此来获得器内的旋转运动。气体在器内按螺旋形路线向器底旋转,到达底部后折而向 上,成为内层的上旋的气流,称为气芯,然后从顶部的中央排气管排出。气体中所夹带的尘 粒在随气流旋转的过程中,由于密度较大,受离心力的作用逐渐沉降到器壁,碰到器壁后落 下,滑向出灰口。 旋风分离器各部分的尺寸都有一定的比例,只要规定出其中一个主要尺寸,如圆筒直径 D 或进气口宽度 B,则其它各部分的尺寸亦确定。 (2)分离性能估计 ①能被分离出的最小颗粒直径——临界直径 dc : 假定:颗粒与气体在旋风分离器内的切线速度 ut 恒定,与所在位置无关,且等于在进 口处的速度 i u ;颗粒沉降过程中所穿过的最大气层厚度等进气口宽度 B;颗粒与气流的相对 运动为层流。 在第三个假设条件下,颗粒沉降速度仍可用 Stokes 公式表示,只是需要将其中重力加 速度换为离心加速度。考虑到气体的密度远小于颗粒的密度,并以气体进口速度 i u 代替切线 速度 ut ,旋转半径取平均值 rm ,则沉降速度可表示为: m s i r r d u u 18 2 2 = 根据第二条假设, 沉降时间= 2 2 18 s i m r d u r B u B = 令气体进入气芯以前在向内旋转的圈数为 N,由运行距离为 2rm N ,故得气体在器内的 有效停留时间为: 停留时间= i m u 2r N 某一粒径的颗粒能 100%地被分离出来的条件是:该粒径的颗粒穿过最大气层厚度所需 要时间小于等于气体在器内的有效停留时间,即

B 18urm B 2mmN -:d2 9μB (6) ur d2pju INuiPs 上式如果取等号,就是恰好能100%被分离出来的颗粒直径,以d,表示。其中气体在器内旋 转圈数N经常取5。 可见,临界直径不仅与颗粒和气体的性质有关,而且与旋风分离器的结构和处理量有关。 处理量越小(u越小)、颗粒密度越大、进口越窄、长径比越大(N越大),则临界直径越小, 或者说越容易分离。 导出该式的假定很勉强,故只属粗略估计。 ②分离效率 粉尘中含有大小不同的颗粒,通过旋风分离器后,各种大小不同的颗粒被分离出的百分 数各不相同,按颗粒大小分别表示出各自被分离的质量分率,此即粒级效率。 显然,直径大于临界直径的颗粒粒级效率均为1。 假设颗粒进入器内时分布完全均匀,则与器壁距离小于B的各种直径的颗粒所占的质 量分率应为B/B。 有些颗粒,虽然直径小于临界直径,但进入器内时它们与器壁的距离小于B,故也可能 被分离。由式(6)可知,能被分离出的颗粒直径与此颗粒距器壁的距离的1/2次成正比。 于是:A B 。考虑式(6)的意义,该式的含意是:进入时离器壁为B的颗粒中,直径 等于d的都能被分离,即n=B/B。于是: n=(dld)2 式中的n即为直径等于d的颗粒的粒级效率。 进入旋风分离器的全部粉尘中实际上能被分离出来的总质量分率,称为总效率。。总 效率不仅与旋风分离器的粒级效率有关,还与进入粉尘的粒度、浓度等有关。 总效率与粒级效率的关系为:no=∑a ③压降:气体经过旋风分离器时,由于进气管和排气管及主体器壁所引起的摩擦阻力、 流动时的局部阻力以及气体旋转运动所产生的能量损失等,都将造成气体的压力降。旋风分 离器的压降大小是评价其性能好坏的重要指标。气体通过旋风分离器的压降应尽可能小。通 常压降用入口气体动能的倍数来表示: 4p=5P 2 其中阻力系数要依据不同的设备用实验测定。已经有人针对教材中所示的设备估计出了阻力 系数的经验式。 16AB D2 (3)送型与计算 3.旋液分离器
i m s i m r u r N d u r B u B 18 2 2 2 = ; Nui s B d 9 (6) 上式如果取等号,就是恰好能 100%被分离出来的颗粒直径,以 dc 表示。其中气体在器内旋 转圈数 N 经常取 5。 可见,临界直径不仅与颗粒和气体的性质有关,而且与旋风分离器的结构和处理量有关。 处理量越小( i u 越小)、颗粒密度越大、进口越窄、长径比越大(N 越大),则临界直径越小, 或者说越容易分离。 导出该式的假定很勉强,故只属粗略估计。 ②分离效率 粉尘中含有大小不同的颗粒,通过旋风分离器后,各种大小不同的颗粒被分离出的百分 数各不相同,按颗粒大小分别表示出各自被分离的质量分率,此即粒级效率。 显然,直径大于临界直径的颗粒粒级效率均为 1。 假设颗粒进入器内时分布完全均匀,则与器壁距离小于 B' 的各种直径的颗粒所占的质 量分率应为 B' / B 。 有些颗粒,虽然直径小于临界直径,但进入器内时它们与器壁的距离小于 B,故也可能 被分离。由式(6)可知,能被分离出的颗粒直径与此颗粒距器壁的距离的 1/2 次成正比。 于是: B B d d c ' = 。考虑式(6)的意义,该式的含意是:进入时离器壁为 B' 的颗粒中,直径 等于 d 的都能被分离,即 = B' / B 。于是: 2 ( / ) = d dc 式中的 即为直径等于 d 的颗粒的粒级效率。 进入旋风分离器的全部粉尘中实际上能被分离出来的总质量分率,称为总效率 O 。总 效率不仅与旋风分离器的粒级效率有关,还与进入粉尘的粒度、浓度等有关。 总效率与粒级效率的关系为: O = aii ③压降:气体经过旋风分离器时,由于进气管和排气管及主体器壁所引起的摩擦阻力、 流动时的局部阻力以及气体旋转运动所产生的能量损失等,都将造成气体的压力降。旋风分 离器的压降大小是评价其性能好坏的重要指标。气体通过旋风分离器的压降应尽可能小。通 常压降用入口气体动能的倍数来表示: 2 2 ui p = 其中阻力系数要依据不同的设备用实验测定。已经有人针对教材中所示的设备估计出了阻力 系数的经验式。 2 1 16 D AB = (3)选型与计算 3.旋液分离器