
第六章 统计热力学初步 引言 玻耳兹曼分布 普通高等教背十一五”国家级规划时材 分子配分函数 物理化学简明教程 分子配分函数 (第四版) 的求算及应用 ■白水形男正借强树华等需 蒂高原出低 高等教育出版社 高等教育电子音像出版社
高等教育出版社 高等教育电子音像出版社 分子配分函数 的求算及应用 玻耳兹曼分布 引言 分子配分函数

§6.1 引言 1.统计热力学的研究对象和方法 2.统计系统的分类 3.统计热力学基本假定 第六章统计热万学初涉 返回目录 退出
第六章 统计热力学初步 返回目录 退出 2 1. 统计热力学的研究对象和方法 3. 统计热力学基本假定 2. 统计系统的分类 §6.1 引言

1.统计热力学的研究对象和方法 研究对象同热力学,大量分子的集合体,即宏观物体 热力学研究方法: 依据几个经验定律,通过逻辑推理的方法导出平衡系 统的宏观性质和变化规律。 特点:其结论有高度的可靠性,且不依赖人们对微观 结构的认识。(知其然不知其所以然 一这正是热力学的 优点,也是其局限性) 统计热力学研究方法:(统计平均的方法) 从分析微观粒子的运动状态入手,用统计平均的方法, 确立微观粒子的运动状态和宏观性质之间的联系。统计热 力学是沟通宏观学科和微观学科的桥梁。 第六章 统计热力学初光 返回目录 退出
第六章 统计热力学初步 返回目录 退出 3 1. 统计热力学的研究对象和方法 研究对象同热力学,大量分子的集合体,即宏观物体 热力学研究方法: 依据几个经验定律,通过逻辑推理的方法导出平衡系 统的宏观性质和变化规律。 特点:其结论有高度的可靠性,且不依赖人们对微观 结构的认识。(知其然不知其所以然——这正是热力学的 优点,也是其局限性) 统计热力学研究方法: (统计平均的方法) 从分析微观粒子的运动状态入手,用统计平均的方法, 确立微观粒子的运动状态和宏观性质之间的联系。统计热 力学是沟通宏观学科和微观学科的桥梁
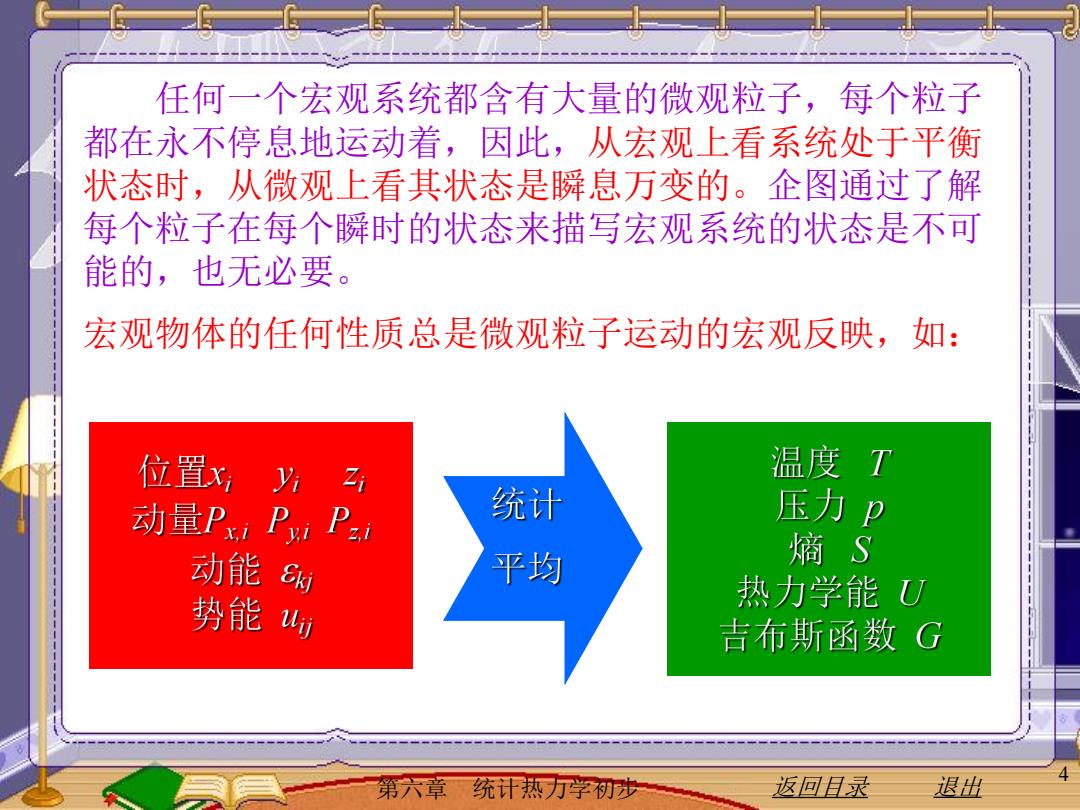
任何一个宏观系统都含有大量的微观粒子,每个粒子 都在永不停息地运动着,因此,从宏观上看系统处于平衡 状态时,从微观上看其状态是瞬息万变的。企图通过了解 每个粒子在每个瞬时的状态来描写宏观系统的状态是不可 能的,也无必要。 宏观物体的任何性质总是微观粒子运动的宏观反映,如: 位置x Zi 温度 T 动量PiPP= 统计 压力 动能 平均 熵S 势能 热力学能U 吉布斯函数G 第六章 统计热万学初光 返回目录 退出
第六章 统计热力学初步 返回目录 退出 4 宏观物体的任何性质总是微观粒子运动的宏观反映,如: 任何一个宏观系统都含有大量的微观粒子,每个粒子 都在永不停息地运动着,因此,从宏观上看系统处于平衡 状态时,从微观上看其状态是瞬息万变的。企图通过了解 每个粒子在每个瞬时的状态来描写宏观系统的状态是不可 能的,也无必要

例如欲求算一个平衡系统的热力学能值, 如果要去求算每个分子在每个瞬时的能量然后 再去加和,这是不可能的。 然而,统计热力学依据微观粒子能量量子化 的概念认为,虽然每个分子在每 一瞬时可以处于 不同的能级,但从平衡系统中大量分子来看,处 于某个能级c,的平均分子数n,却是一定的。 因此U=∑n,8,。这样求出的宏观系统热力学 能当然不是瞬时值而是统计平均值 统计平均的方法是统计热力学的基本特点。 第六章 统计热力学初光 返回目录 退出
第六章 统计热力学初步 返回目录 退出 5 例如欲求算一个平衡系统的热力学能U值, 如果要去求算每个分子在每个瞬时的能量然后 再去加和,这是不可能的。 然而,统计热力学依据微观粒子能量量子化 的概念认为,虽然每个分子在每一瞬时可以处于 不同的能级,但从平衡系统中大量分子来看,处 于某个能级εi的平均分子数ni却是一定的。 因此U=Σniεi。这样求出的宏观系统热力学 能当然不是瞬时值而是统计平均值。 统计平均的方法是统计热力学的基本特点

将统计热力学原理应用于结构比较简单的 系统,如低压气体,原子晶体等,其计算结果 与实验测量值能很好地吻合。但在处理结构比 较复杂的系统时,统计热力学常会遇到种种困 难,因而不得不作一些近似假设,其结果往往 不如热力学那样准确可靠。此外,在统计热力 学计算中常常要用到一些热力学的基本关系和 公式,所以可以说热力学和统计热力学是相互 补充、相辅相成的。 第六章 统计热万学初光 返回目录 退出
第六章 统计热力学初步 返回目录 退出 6 将统计热力学原理应用于结构比较简单的 系统,如低压气体,原子晶体等,其计算结果 与实验测量值能很好地吻合。但在处理结构比 较复杂的系统时,统计热力学常会遇到种种困 难,因而不得不作一些近似假设,其结果往往 不如热力学那样准确可靠。此外,在统计热力 学计算中常常要用到一些热力学的基本关系和 公式,所以可以说热力学和统计热力学是相互 补充、相辅相成的

2.统计系统的分类 (1)按照粒子是否可辩,或是否有确定位置分为: 定域子系统,或称定位系统,可辨粒子系统。 如原子晶体: 离域子系统,或称非定位系统,等同粒子系统。 如气体。 (2)按照粒子之间有无相互作用力,又可分为: 独立粒子系统,如理想气体; 非独立粒子系统,如实际气体。 第六章 统计热万了学初光 返回目录 退出
第六章 统计热力学初步 返回目录 退出 7 2. 统计系统的分类 (1)按照粒子是否可辩,或是否有确定位置分为: 定域子系统,或称定位系统,可辨粒子系统。 如原子晶体; 离域子系统,或称非定位系统,等同粒子系统。 如气体。 (2)按照粒子之间有无相互作用力,又可分为: 独立粒子系统,如理想气体; 非独立粒子系统,如实际气体

3.统计热力学基本假定 假定某系统有4个可辨粒子a、b、c、d,分配于两个相连的、 容积相等的空间及Ⅱ之中,所有可能的分配形式如下表所列 表6.14个可辨粒子分配于两个等容积空间的分配形式 分布方式 空间I 空间Ⅲ 微观状态数 数学概率 (4,0)分布 abed C4=1 16 (3,1)分布 abc abd d C=4 acd bcd b a 1 (2,2)分布 ab bc cd ad ac bd bd ac C=6 ad cd bc ab (1,3)分布 d C abc abd b C4=4 a acd bcd 46 (0,4)分布 abed 1 C9=1 16 返回目录 8 第六章统计热万学初步 退出
第六章 统计热力学初步 返回目录 退出 8 3. 统计热力学基本假定 假定某系统有4个可辨粒子a、b、c、d,分配于两个相连的、 容积相等的空间I及II之中,所有可能的分配形式如下表所列 分布方式 空间I 空间II 微观状态数 数学概率 (4,0)分布 abcd (3,1)分布 a b c a b d d c a c d b c d b a (2,2)分布 a b bc c d a d a c bd b d a c a d c d b c a b (1,3)分布 d c a b c a b d b a a c d b c d (0,4)分布 abcd 1 4 C4 4 3 C4 6 2 C4 4 1 C4 1 0 C4 16 1 16 4 16 6 16 4 16 1 表6.1 4个可辨粒子分配于两个等容积空间的分配形式

表6.1中列出的每一种可能的分配形式称为一个微观状 态,所有可能的分配形式总数称为系统的总微观状态数, 用2表示。由表6.1可见,上述系统的总微观状态数2=16 统计热力学认为:“对于宏观处于一定平衡状态的系 统而言,任何一个可能出现的微观状态都具有相同的数学 概率”。也就是说,在众多的可能出现的微观状态中,任 何一个都没有明显理由比其它微观状态更可能出现,这称 为等概率假定。 等概率假定是统计热力学的基本假定。这个假定的 合理性已经由其引出的结论与实际相符而得到证明。根 据等概率假定,上例中每一个微观状态出现的数学概率 都是1/16。 第六章 统计热力学初涉 返回目录 退出
第六章 统计热力学初步 返回目录 退出 9 表6.1中列出的每一种可能的分配形式称为一个微观状 态,所有可能的分配形式总数称为系统的总微观状态数, 用Ω表示。由表6.1可见,上述系统的总微观状态数Ω =16 统计热力学认为: “对于宏观处于一定平衡状态的系 统而言,任何一个可能出现的微观状态都具有相同的数学 概率” 。也就是说,在众多的可能出现的微观状态中,任 何一个都没有明显理由比其它微观状态更可能出现,这称 为等概率假定。 等概率假定是统计热力学的基本假定。这个假定的 合理性已经由其引出的结论与实际相符而得到证明。根 据等概率假定,上例中每一个微观状态出现的数学概率 都是1/16

微观状态数(热力学概率)2, 根据等概率假定,在N,U,V一定的系统中,每一个微观 状态出现的概率相等。因此,某种分布所拥有的微观状态 数目可以度量该种分布出现的可能性的大小。在统计热 力学中,将一定的宏观状态或能量分布所拥有的微观状态 数2,定义为它们的热力学概率。 2=∑ 热力学概率和概率不同,前者为正整数;而后者则通常 小于1,为分数: 如某分布,它的热力学概率为, 而概率P=/2 第六章 统计热万学初光 返回目录 退出
第六章 统计热力学初步 返回目录 退出 10 微观状态数(热力学概率)Ω,tj 根据等概率假定,在N,U,V一定的系统中,每一个微观 状态出现的概率相等。因此,某种分布所拥有的微观状态 数目tj 可以度量该种分布出现的可能性的大小。在统计热 力学中,将一定的宏观状态或能量分布所拥有的微观状态 数Ω, tj定义为它们的热力学概率。 热力学概率和概率不同,前者为正整数;而后者则通常 小于1,为分数: 如某分布j,它的热力学概率为tj , 而概率 Pj = tj /Ω Ω=Σ tj