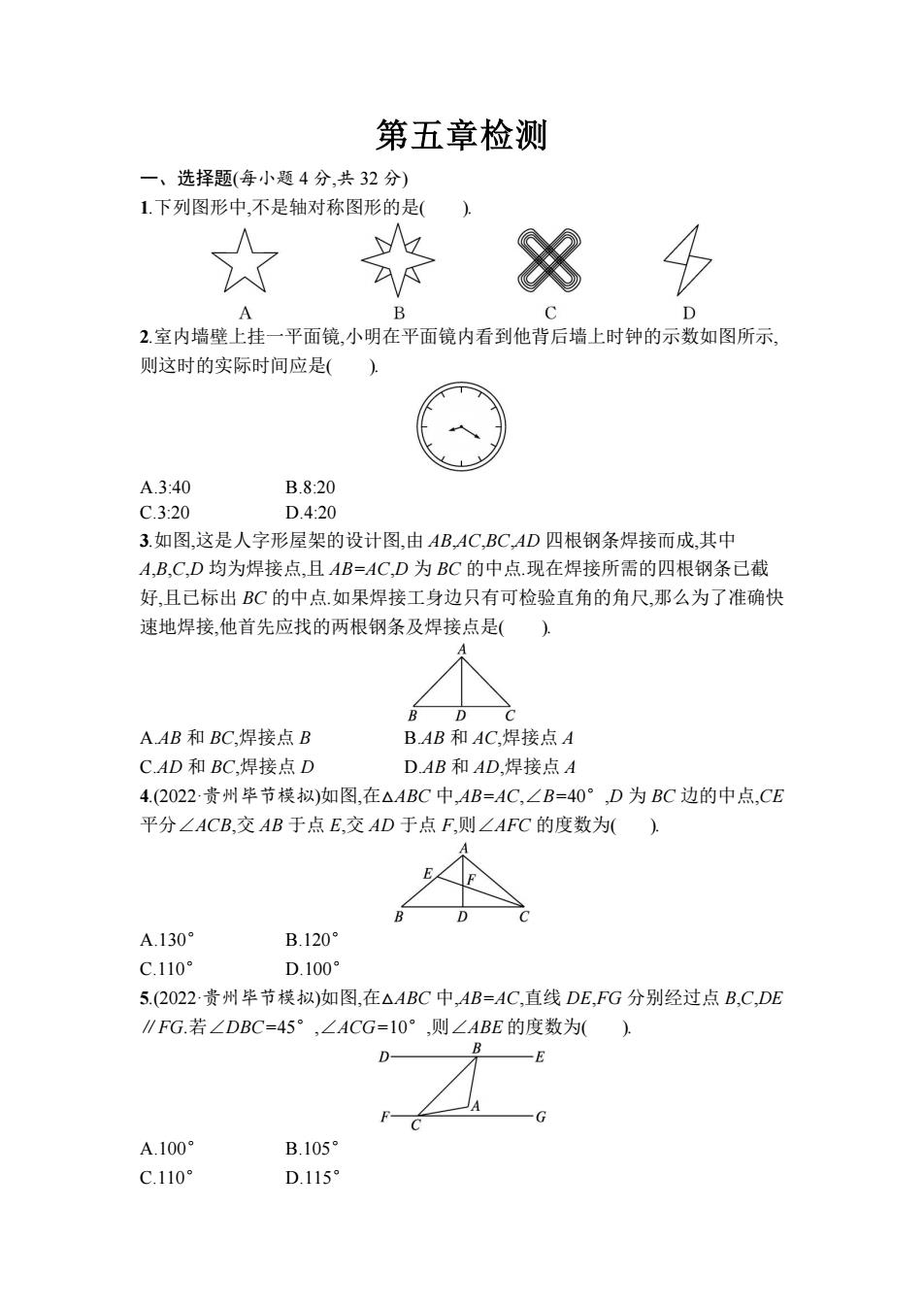
第五章检测 一、选择题(每小题4分,共32分) 1.下列图形中,不是轴对称图形的是( A 2.室内墙壁上挂一平面镜,小明在平面镜内看到他背后墙上时钟的示数如图所示, 则这时的实际时间应是() A.3:40 B.820 C.3:20 D.4:20 3.如图,这是人字形屋架的设计图,由AB,AC,BC,AD四根钢条焊接而成,其中 A,B,C,D均为焊接点,且AB=AC,D为BC的中点现在焊接所需的四根钢条已截 好,且已标出BC的中点如果焊接工身边只有可检验直角的角尺,那么为了准确快 速地焊接,他首先应找的两根钢条及焊接点是( D A.AB和BC,焊接点B B.AB和AC,焊接点A C.AD和BC,焊接点D D.AB和AD,焊接点A 4.(2022贵州毕节模拟)如图,在△ABC中,AB=AC,∠B=40°,D为BC边的中点,CE 平分∠ACB,交AB于点E,交AD于点F,则∠AFC的度数为() A.130 B.120° C.110° D.100 5.(2022贵州毕节模拟)如图,在△ABC中,AB=AC,直线DE,FG分别经过点B,C,DE ∥FG.若∠DBC=45°,∠ACG=10°,则∠ABE的度数为() B D 一E A.100 B.105° C.110° D.115
第五章检测 一、选择题(每小题 4 分,共 32 分) 1.下列图形中,不是轴对称图形的是( ). 2.室内墙壁上挂一平面镜,小明在平面镜内看到他背后墙上时钟的示数如图所示, 则这时的实际时间应是( ). A.3:40 B.8:20 C.3:20 D.4:20 3.如图,这是人字形屋架的设计图,由 AB,AC,BC,AD 四根钢条焊接而成,其中 A,B,C,D 均为焊接点,且 AB=AC,D 为 BC 的中点.现在焊接所需的四根钢条已截 好,且已标出 BC 的中点.如果焊接工身边只有可检验直角的角尺,那么为了准确快 速地焊接,他首先应找的两根钢条及焊接点是( ). A.AB 和 BC,焊接点 B B.AB 和 AC,焊接点 A C.AD 和 BC,焊接点 D D.AB 和 AD,焊接点 A 4.(2022·贵州毕节模拟)如图,在△ABC 中,AB=AC,∠B=40°,D 为 BC 边的中点,CE 平分∠ACB,交 AB 于点 E,交 AD 于点 F,则∠AFC 的度数为( ). A.130° B.120° C.110° D.100° 5.(2022·贵州毕节模拟)如图,在△ABC 中,AB=AC,直线 DE,FG 分别经过点 B,C,DE ∥FG.若∠DBC=45°,∠ACG=10°,则∠ABE 的度数为( ). A.100° B.105° C.110° D.115°

6.(2022贵州铜仁模拟)△ABC中,AB=AC,∠A=36°,若按如图的尺规作图方法作 出线段BD,则下列结论错误的是( A.AD=BD B.C△BCD=AB+BC C.∠BDC=72 D.S△ABD:SABCD=BC:AC 7.已知等腰三角形的一边长等于4,一边长等于9,则它的周长为() A.9 B.17或22 C.17 D.22 8.如图,DG,EH分别是BF,FC的垂直平分线.有下列结论:①△BDF,△CEF都是等 腰三角形:,②DE=BD+CE,③△ADE的周长为AB+AC,④BD=CE其中正确的是 () A.③④ B.①② C.①②③ D.②③④ 二、填空题(每小题4分,共24分) 9.如图,在△ABC中,点D在BC边上,BD=AD=AC,E为CD的中点.若∠ CAE=16°,则∠B为 B DE C 10.如图,在△ABC中,AB=AC,点D,E都在边BC上,∠BAD=∠CAE.若BD=9,则CE 的长为 B D E C 11.下列说法正确的是 (把所有正确的序号都填到空里) ①角平分线上的任意一点到角两边的线段的长度相等:②角是轴对称图形:③线段 不是轴对称图形,④线段垂直平分线上的点到这条线段两个端点的距离相等
6.(2022·贵州铜仁模拟)△ABC 中,AB=AC,∠A=36°,若按如图的尺规作图方法作 出线段 BD,则下列结论错误的是( ). A.AD=BD B.C△BCD=AB+BC C.∠BDC=72° D.S△ABD∶S△BCD=BC∶AC 7.已知等腰三角形的一边长等于 4,一边长等于 9,则它的周长为( ). A.9 B.17 或 22 C.17 D.22 8.如图,DG,EH 分别是 BF,FC 的垂直平分线.有下列结论:①△BDF,△CEF 都是等 腰三角形;②DE=BD+CE;③△ADE 的周长为 AB+AC;④BD=CE.其中正确的是 ( ). A.③④ B.①② C.①②③ D.②③④ 二、填空题(每小题 4 分,共 24 分) 9.如图,在△ABC 中,点 D 在 BC 边上,BD=AD=AC,E 为 CD 的中点.若∠ CAE=16°,则∠B 为 . 10.如图,在△ABC 中,AB=AC,点 D,E 都在边 BC 上,∠BAD=∠CAE.若 BD=9,则 CE 的长为 . 11.下列说法正确的是 .(把所有正确的序号都填到空里) ①角平分线上的任意一点到角两边的线段的长度相等;②角是轴对称图形;③线段 不是轴对称图形;④线段垂直平分线上的点到这条线段两个端点的距离相等
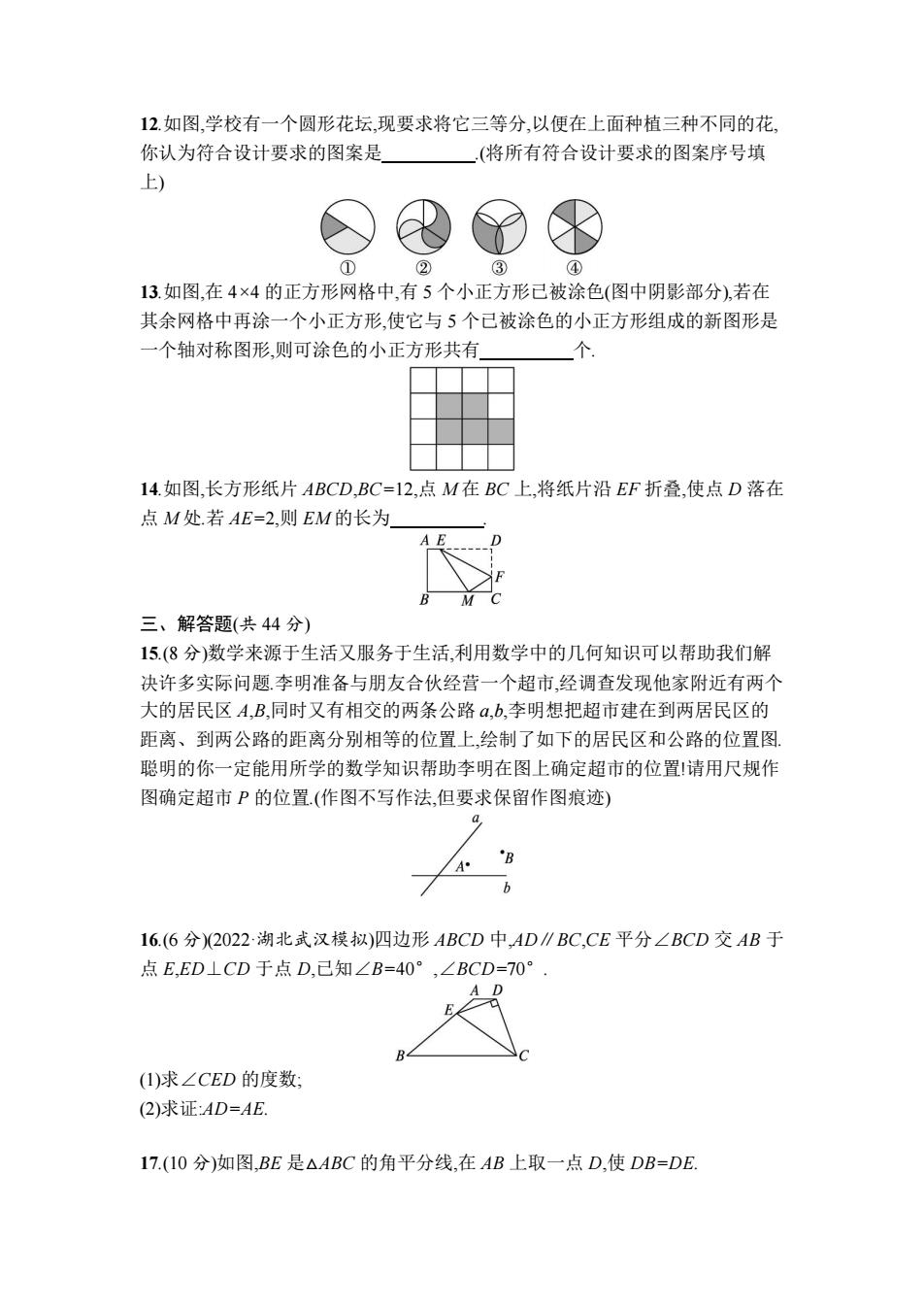
12.如图,学校有一个圆形花坛,现要求将它三等分,以便在上面种植三种不同的花 你认为符合设计要求的图案是 (将所有符合设计要求的图案序号填 上) ① ② ③ ④ 13.如图,在4×4的正方形网格中,有5个小正方形已被涂色(图中阴影部分),若在 其余网格中再涂一个小正方形,使它与5个已被涂色的小正方形组成的新图形是 一个轴对称图形,则可涂色的小正方形共有 个 14.如图,长方形纸片ABCD,BC=12,点M在BC上,将纸片沿EF折叠,使点D落在 点M处.若AE=2,则EM的长为 三、解答题(共44分) 15.(8分)数学来源于生活又服务于生活,利用数学中的几何知识可以帮助我们解 决许多实际问题李明准备与朋友合伙经营一个超市,经调查发现他家附近有两个 大的居民区A,B,同时又有相交的两条公路α,b,李明想把超市建在到两居民区的 距离、到两公路的距离分别相等的位置上,绘制了如下的居民区和公路的位置图 聪明的你一定能用所学的数学知识帮助李明在图上确定超市的位置!请用尺规作 图确定超市P的位置.(作图不写作法,但要求保留作图痕迹) A 16.(6分)(2022·湖北武汉模拟)四边形ABCD中,AD∥BC,CE平分∠BCD交AB于 点E,ED⊥CD于点D,己知∠B=40°,∠BCD=70°. A D (1)求∠CED的度数: (2)求证:AD=AE, 17.(I0分)如图,BE是△ABC的角平分线,在AB上取一点D,使DB=DE
12.如图,学校有一个圆形花坛,现要求将它三等分,以便在上面种植三种不同的花, 你认为符合设计要求的图案是 .(将所有符合设计要求的图案序号填 上) 13.如图,在 4×4 的正方形网格中,有 5 个小正方形已被涂色(图中阴影部分),若在 其余网格中再涂一个小正方形,使它与 5 个已被涂色的小正方形组成的新图形是 一个轴对称图形,则可涂色的小正方形共有 个. 14.如图,长方形纸片 ABCD,BC=12,点 M 在 BC 上,将纸片沿 EF 折叠,使点 D 落在 点 M 处.若 AE=2,则 EM 的长为 . 三、解答题(共 44 分) 15.(8 分)数学来源于生活又服务于生活,利用数学中的几何知识可以帮助我们解 决许多实际问题.李明准备与朋友合伙经营一个超市,经调查发现他家附近有两个 大的居民区 A,B,同时又有相交的两条公路 a,b,李明想把超市建在到两居民区的 距离、到两公路的距离分别相等的位置上,绘制了如下的居民区和公路的位置图. 聪明的你一定能用所学的数学知识帮助李明在图上确定超市的位置!请用尺规作 图确定超市 P 的位置.(作图不写作法,但要求保留作图痕迹) 16.(6 分)(2022·湖北武汉模拟)四边形 ABCD 中,AD∥BC,CE 平分∠BCD 交 AB 于 点 E,ED⊥CD 于点 D,已知∠B=40°,∠BCD=70°. (1)求∠CED 的度数; (2)求证:AD=AE. 17.(10 分)如图,BE 是△ABC 的角平分线,在 AB 上取一点 D,使 DB=DE

(I)求证:DE∥BC; (2)若∠A=65°,∠AED=45°,求∠EBC的度数 18.(I0分)已知△ABC是等边三角形,过点C作CD∥AB,且CD=AB,连接BD,交 AC于点O (I)如图①,试说明:AC垂直平分BD (2)如图②,点M在BC的延长线上,点N在线段CO上,且ND=NM连接BN.试说 明:NB=NM 图① 图② 19.(10分)如图,在等边三角形ABC中,点D在BC边上,点E在AC的延长线 上,DE=DA (I)试说明∠BAD=∠EDC (2)作出点E关于直线BC的对称点M,连接DM,AM,猜想DM与AM的数量关系 并说明理由 答案: 一、选择题 1.D2.A3.C4.C5.A6.D7.D8.C 二、填空题 9.37°10.911.②④12.②③④13.414.10 三、解答题 15解:如图,P点即为超市位置
(1)求证:DE∥BC; (2)若∠A=65°,∠AED=45°,求∠EBC 的度数. 18.(10 分)已知△ABC 是等边三角形,过点 C 作 CD∥AB,且 CD=AB,连接 BD,交 AC 于点 O. (1)如图①,试说明:AC 垂直平分 BD. (2)如图②,点 M 在 BC 的延长线上,点 N 在线段 CO 上,且 ND=NM,连接 BN.试说 明:NB=NM. 图① 图② 19.(10 分)如图,在等边三角形 ABC 中,点 D 在 BC 边上,点 E 在 AC 的延长线 上,DE=DA. (1)试说明∠BAD=∠EDC; (2)作出点 E 关于直线 BC 的对称点 M,连接 DM,AM,猜想 DM 与 AM 的数量关系, 并说明理由. 答案: 一、选择题 1.D 2.A 3.C 4.C 5.A 6.D 7.D 8.C 二、填空题 9.37° 10.9 11.②④ 12.②③④ 13.4 14.10 三、解答题 15.解:如图,P 点即为超市位置

16.(I)解:,CE平分∠BCD交AB于点E,∠BCD=70°, ∴.∠BCE=∠DCE=35°, ,ED⊥CD于点D, .∠CDE=90°, ∴.∠CED=90°-∠DCE=55°; (2)证明过E点作EF∥BC, ∴.∠CEF=∠BCE=35°,∠AEF=∠B=40° ∴.∠DEF=∠CED-∠CEF-55°-35°=20°, ∴.∠AED=∠AEF-∠DEF-20°, ,AD∥BC .AD∥EF, ∴.∠ADE=∠DEF=20°, ∴.∠AED=∠ADE ..AD=AE 17.(1)证明,BE是△ABC的角平分线, ∠DBE=∠EBC,,DB=DE .∠DEB=∠DBE,∴.∠DEB=∠EBC, .DE∥BC (2)解:.DE∥BC, ∴.∠C=∠AED=45° 在△ABC中,∠A+∠ABC+∠C=180° .∠ABC=180°-∠A-∠C=180°-65°-45°=70° ,BE是△ABC的角平分线, ∴∠DBE=∠EBC=∠ABC=35° 18.解:(1)因为△ABC是等边三角形 所以AB=BC,∠A=60° 因为CD=AB,所以CD=BC, 即△BCD为等腰三角形 因为CD∥AB,所以∠ACD=∠A=60°, 所以∠BCO=∠OCD, 所以BO=DO,CO⊥BD
16.(1)解:∵CE 平分∠BCD 交 AB 于点 E,∠BCD=70°, ∴∠BCE=∠DCE=35°, ∵ED⊥CD 于点 D, ∴∠CDE=90°, ∴∠CED=90°-∠DCE=55°; (2)证明 过 E 点作 EF∥BC, ∴∠CEF=∠BCE=35°,∠AEF=∠B=40°, ∴∠DEF=∠CED-∠CEF=55°-35°=20°, ∴∠AED=∠AEF-∠DEF=20°, ∵AD∥BC, ∴AD∥EF, ∴∠ADE=∠DEF=20°, ∴∠AED=∠ADE, ∴AD=AE. 17.(1)证明 ∵BE 是△ABC 的角平分线, ∴∠DBE=∠EBC,∵DB=DE, ∴∠DEB=∠DBE,∴∠DEB=∠EBC, ∴DE∥BC. (2)解:∵DE∥BC, ∴∠C=∠AED=45°. 在△ABC 中,∠A+∠ABC+∠C=180°, ∴∠ABC=180°-∠A-∠C=180°-65°-45°=70°. ∵BE 是△ABC 的角平分线, ∴∠DBE=∠EBC=1 2∠ABC=35°. 18.解:(1)因为△ABC 是等边三角形, 所以 AB=BC,∠A=60°. 因为 CD=AB,所以 CD=BC, 即△BCD 为等腰三角形. 因为 CD∥AB,所以∠ACD=∠A=60°, 所以∠BCO=∠OCD, 所以 BO=DO,CO⊥BD

即AC垂直平分BD. (2)由(1)知AC垂直平分BD, 所以NB=ND 因为ND=NM所以NB=NM 19.解:(1),△ABC是等边三角形, ∴.∠BAC=∠ACB=60° ,∠BAD+∠DAC=∠BAC, ∠ACB+∠DCE=180°, ∠DEC+∠CDE+∠DCE=180°, ∴.∠EDC+∠DEC=∠ACB, ∴.∠BAD+∠DAC=∠EDC+∠DEC .DE=DA, ∴.∠DAC=∠DEC ∴∠BAD=∠EDC (2)猜想:DM=AM理由如下: ,点M,E关于直线BC对称, ∴.∠MDC=∠EDC,DE=DM 又由(I)知∠BAD=∠EDC, ∴.∠MDC=∠BAD ,∠ADB+∠BAD+∠B=180°,∠ADB+∠ADC=180°, ∴.∠ADC=∠BAD+∠B 即∠ADM+∠MDC=∠BAD+∠B, ∴.∠ADM=∠B=60° .DA=DE=DM, .△ADM是等边三角形, ∴.DM=AM
即 AC 垂直平分 BD. (2)由(1)知 AC 垂直平分 BD, 所以 NB=ND. 因为 ND=NM,所以 NB=NM. 19.解:(1)∵△ABC 是等边三角形, ∴∠BAC=∠ACB=60°. ∵∠BAD+∠DAC=∠BAC, ∠ACB+∠DCE=180°, ∠DEC+∠CDE+∠DCE=180°, ∴∠EDC+∠DEC=∠ACB, ∴∠BAD+∠DAC=∠EDC+∠DEC. ∵DE=DA, ∴∠DAC=∠DEC, ∴∠BAD=∠EDC. (2)猜想:DM=AM.理由如下: ∵点 M,E 关于直线 BC 对称, ∴∠MDC=∠EDC,DE=DM. 又由(1)知∠BAD=∠EDC, ∴∠MDC=∠BAD. ∵∠ADB+∠BAD+∠B=180°,∠ADB+∠ADC=180°, ∴∠ADC=∠BAD+∠B, 即∠ADM+∠MDC=∠BAD+∠B, ∴∠ADM=∠B=60°. ∵DA=DE=DM, ∴△ADM 是等边三角形, ∴DM=AM