
第四章检测 一、选择题(每小题4分,共32分) 1.如图,AD是△ABC的外角∠EAC的平分线,AD∥BC,∠B=32°,则∠C的度数是 (ù B A.64° B.32 C.30 D.40° 2.桥梁上的拉杆、电视塔的底座都是三角形结构,而活动挂架是四边形结构,它们 分别利用了( ) A.三角形的稳定性,四边形的稳定性 B.三角形的稳定性,四边形的不稳定性 C.三角形的不稳定性,四边形的稳定性 D.三角形的不稳定性,四边形的不稳定性 3.如图,点B,F,C,E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍 无法判定AABC≌△DEF的是( A.∠A=∠D B.AC=DF C.AB=ED D.BF=EC 4.若三角形两边长分别为6cm,2cm,第三边长为偶数,则第三边长为(), A.2 cm B.4 cm C.6 cm D.8 cm 5.下列图形:①两个正方形:②每边长都是1cm的两个四边形:③每边都是2cm的 两个三角形:④半径都是1.5cm的两个圆.其中是一对全等图形的是(). A.①② B.③④ C.①③ D.②④ 6.如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块与原 来完全一样的玻璃,则最省事的办法是( 2 A.带①去 B.带②去 C.带③去 D.带①②去 7.如图,在△ABC中,BE是中线,AD是角平分线,AD与BE相交于点O,连接DE.下 列结论正确的有()
第四章检测 一、选择题(每小题 4 分,共 32 分) 1.如图,AD 是△ABC 的外角∠EAC 的平分线,AD∥BC,∠B=32°,则∠C 的度数是 ( ). A.64° B.32° C.30° D.40° 2.桥梁上的拉杆、电视塔的底座都是三角形结构,而活动挂架是四边形结构,它们 分别利用了( ). A.三角形的稳定性,四边形的稳定性 B.三角形的稳定性,四边形的不稳定性 C.三角形的不稳定性,四边形的稳定性 D.三角形的不稳定性,四边形的不稳定性 3.如图,点 B,F,C,E 在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍 无法判定△ABC≌△DEF 的是( ). A.∠A=∠D B.AC=DF C.AB=ED D.BF=EC 4.若三角形两边长分别为 6 cm,2 cm,第三边长为偶数,则第三边长为( ). A.2 cm B.4 cm C.6 cm D.8 cm 5.下列图形:①两个正方形;②每边长都是 1 cm 的两个四边形;③每边都是 2 cm 的 两个三角形;④半径都是 1.5 cm 的两个圆.其中是一对全等图形的是( ). A.①② B.③④ C.①③ D.②④ 6.如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块与原 来完全一样的玻璃,则最省事的办法是( ). A.带①去 B.带②去 C.带③去 D.带①②去 7.如图,在△ABC 中,BE 是中线,AD 是角平分线,AD 与 BE 相交于点 O,连接 DE.下 列结论正确的有( )

①AO是△ABE的中线;②BO是△ABD的角平分线;③DE是△ADC的中线;④ED 是△EBC的中线, A.1个 B.2个 C.3个 D.4个 8.如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连 接AC,BD交于点M,连接OM下列结论:①AC=BD:②∠AMB=40°;③OM平分∠ BOC,④MO平分∠BMC.其中正确的个数为( A.4 B.3 C.2 D.1 二、填空题(每小题4分,共24分) 9.如图,在△ABC中,CD平分∠ACB,DE∥BC,交AC于点E.若∠AED=50°,则∠D 的度数为 I0.如图,∠AED=∠ACE,∠DAB=∠CAE,要使△ABC≌△ADE,应添加的条件 是 (添加一个条件即可) 1L.如图,在四边形ABCD中,∠A=45°,直线I与边AB,AD分别相交于点M,N,则 ∠1+∠2= 12.若三角形的三边长分别为a,b,5,其中a,b为正整数,且a≤b≤5,则所有满足条 件的三角形共有 个 13.如图,四边形ACDF是正方形,∠CEA和∠ABF都是直角,且点E,A,B三点共 线,AB=4,则阴影部分的面积是
①AO 是△ABE 的中线;②BO 是△ABD 的角平分线;③DE 是△ADC 的中线;④ED 是△EBC 的中线. A.1 个 B.2 个 C.3 个 D.4 个 8.如图,在△OAB 和△OCD 中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连 接 AC,BD 交于点 M,连接 OM.下列结论:①AC=BD;②∠AMB=40°;③OM 平分∠ BOC;④MO 平分∠BMC.其中正确的个数为( ). A.4 B.3 C.2 D.1 二、填空题(每小题 4 分,共 24 分) 9.如图,在△ABC 中,CD 平分∠ACB,DE∥BC,交 AC 于点 E.若∠AED=50°,则∠D 的度数为 . 10.如图,∠AED=∠ACE,∠DAB=∠CAE,要使△ABC≌△ADE,应添加的条件 是 .(添加一个条件即可) 11.如图,在四边形 ABCD 中,∠A=45°,直线 l 与边 AB,AD 分别相交于点 M,N,则 ∠1+∠2= . 12.若三角形的三边长分别为 a,b,5,其中 a,b 为正整数,且 a≤b≤5,则所有满足条 件的三角形共有 个. 13.如图,四边形 ACDF 是正方形,∠CEA 和∠ABF 都是直角,且点 E,A,B 三点共 线,AB=4,则阴影部分的面积是
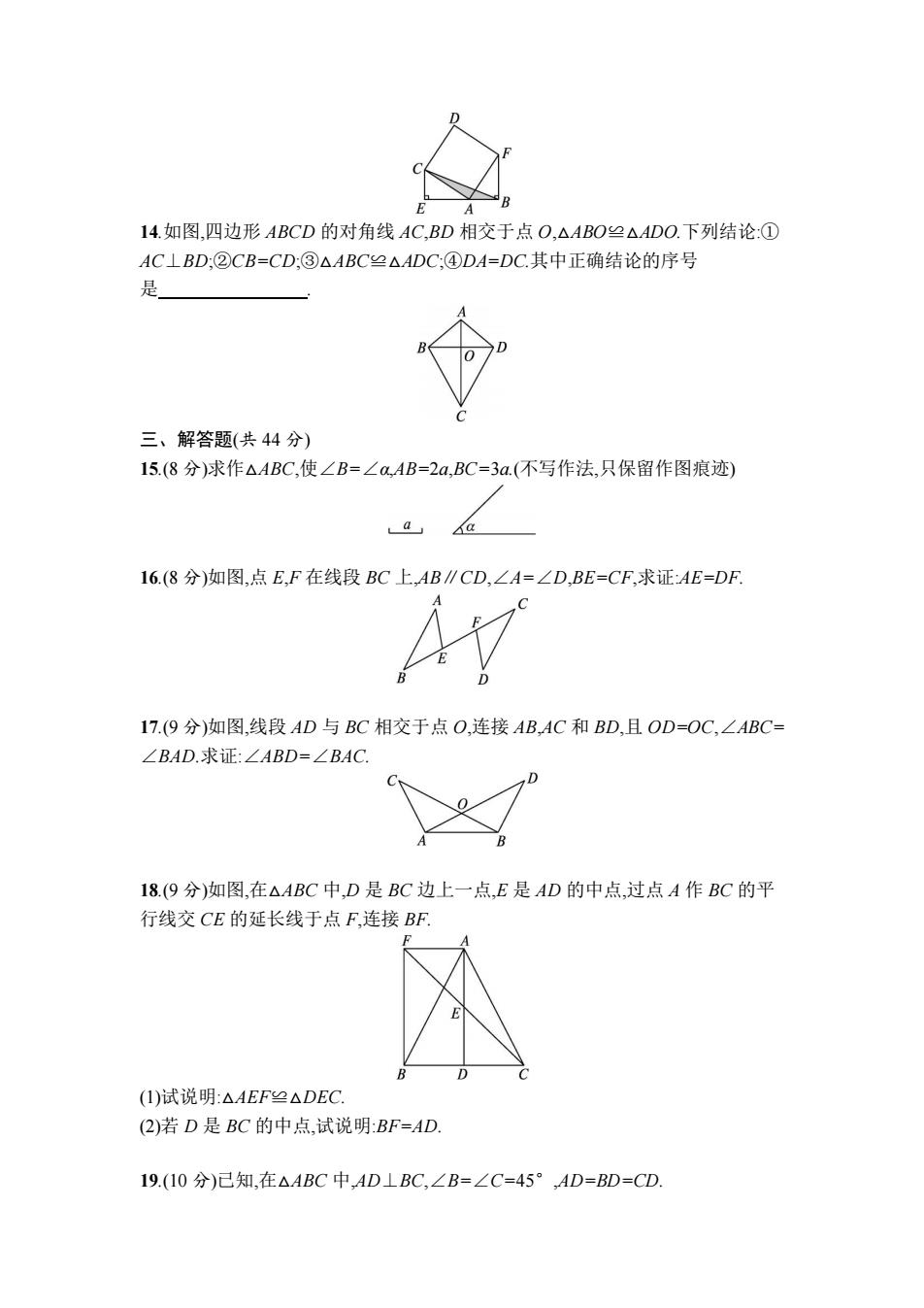
E A 14.如图,四边形ABCD的对角线AC,BD相交于点O,△ABO≌△ADO.下列结论:① AC⊥BD:②CB=CD:③△ABC2△ADC,④DA=DC.其中正确结论的序号 是 三、解答题(共44分) 15.(8分)求作△ABC,使∠B=∠a,AB=2a,BC=3a.(不写作法,只保留作图痕迹) 16.(8分)如图,点E,F在线段BC上,AB∥CD,∠A=∠D,BE=CF,求证:AE=DF 17.(9分)如图,线段AD与BC相交于点O,连接AB,AC和BD,且OD=OC,∠ABC= ∠BAD.求证:∠ABD=∠BAC 18.(9分)如图,在△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平 行线交CE的延长线于点F,连接BF (1)试说明:△AEF≌△DEC. (2)若D是BC的中点,试说明:BF=AD 19.(10分)已知,在△ABC中,AD⊥BC,∠B=∠C=45°,AD=BD=CD
14.如图,四边形 ABCD 的对角线 AC,BD 相交于点 O,△ABO≌△ADO.下列结论:① AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.其中正确结论的序号 是 . 三、解答题(共 44 分) 15.(8 分)求作△ABC,使∠B=∠α,AB=2a,BC=3a.(不写作法,只保留作图痕迹) 16.(8 分)如图,点 E,F 在线段 BC 上,AB∥CD,∠A=∠D,BE=CF,求证:AE=DF. 17.(9 分)如图,线段 AD 与 BC 相交于点 O,连接 AB,AC 和 BD,且 OD=OC,∠ABC= ∠BAD.求证:∠ABD=∠BAC. 18.(9 分)如图,在△ABC 中,D 是 BC 边上一点,E 是 AD 的中点,过点 A 作 BC 的平 行线交 CE 的延长线于点 F,连接 BF. (1)试说明:△AEF≌△DEC. (2)若 D 是 BC 的中点,试说明:BF=AD. 19.(10 分)已知,在△ABC 中,AD⊥BC,∠B=∠C=45°,AD=BD=CD
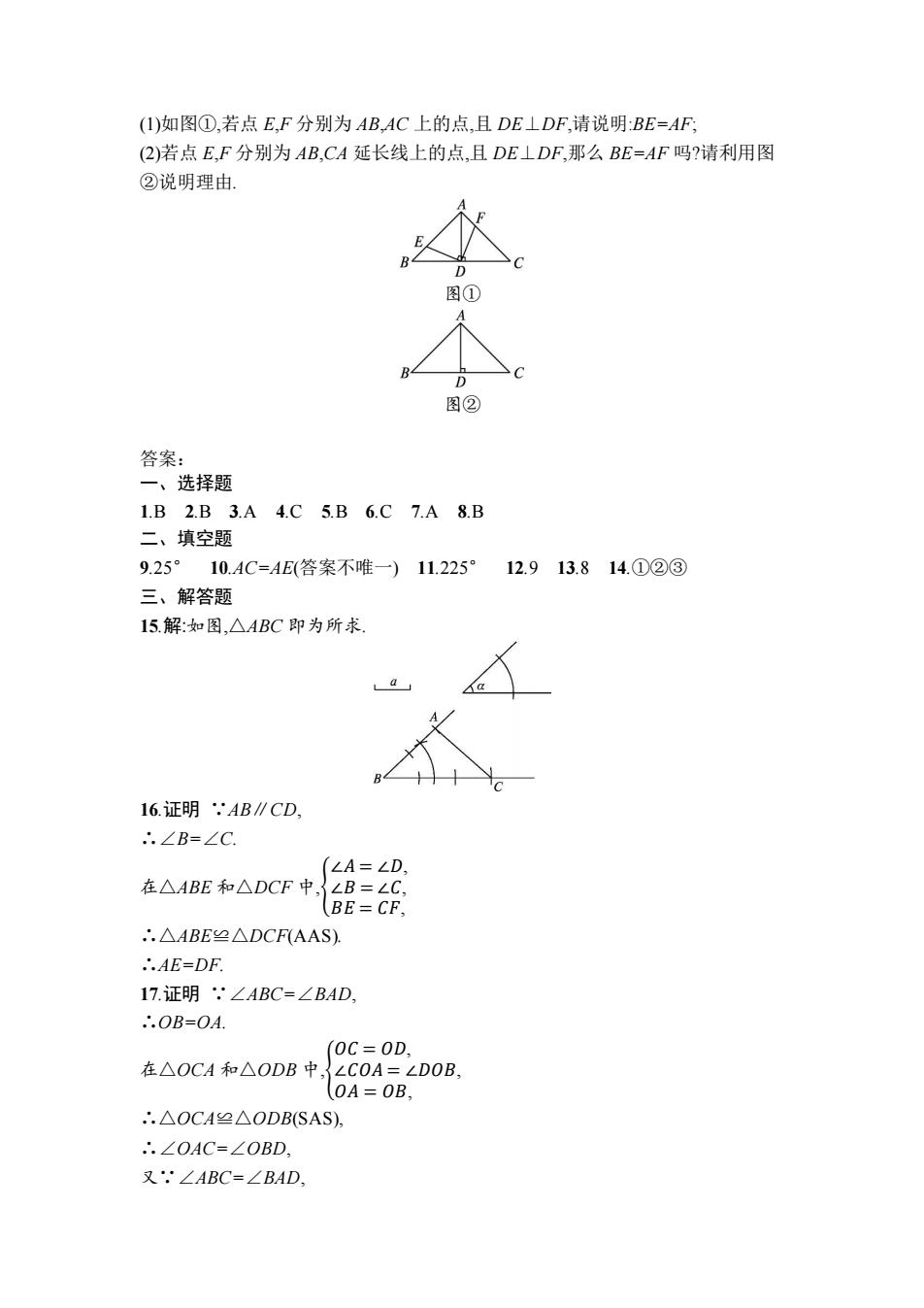
(I)如图①,若点E,F分别为AB,AC上的点,且DE⊥DF,请说明:BE=AF, (2)若点E,F分别为AB,CA延长线上的点,且DE⊥DF,那么BE=AF吗?请利用图 ②说明理由. 图① B D 图② 答案: 一、选择题 1.B2.B3.A4.C5.B6.C7.A8.B 二、填空题 9.25°10.AC=AE(答案不唯一)11.225°12.913.8 14.①②③ 三、解答题 15.解:如图,△ABC即为所求. 16.证明,AB∥CD, ∴.∠B=∠C ∠A=∠D 在△ABE和△DCF中, ∠B=LC BE=CF. .△ABE≌△DCF(AAS). ∴.AE=DF 17.证明.'∠ABC=∠BAD, ∴.OB=OA 0C=0D, 在△OCA和△ODB中,LC0A=LD0B, 0A=0B, ∴.△OCA≌△ODB(SAS), ∴.∠OAC=∠OBD, 又∠ABC=∠BAD
(1)如图①,若点 E,F 分别为 AB,AC 上的点,且 DE⊥DF,请说明:BE=AF; (2)若点 E,F 分别为 AB,CA 延长线上的点,且 DE⊥DF,那么 BE=AF 吗?请利用图 ②说明理由. 图① 图② 答案: 一、选择题 1.B 2.B 3.A 4.C 5.B 6.C 7.A 8.B 二、填空题 9.25° 10.AC=AE(答案不唯一) 11.225° 12.9 13.8 14.①②③ 三、解答题 15.解:如图,△ABC 即为所求. 16.证明 ∵AB∥CD, ∴∠B=∠C. 在△ABE 和△DCF 中,{ ∠𝐴 = ∠𝐷, ∠𝐵 = ∠𝐶, 𝐵𝐸 = 𝐶𝐹, ∴△ABE≌△DCF(AAS). ∴AE=DF. 17.证明 ∵∠ABC=∠BAD, ∴OB=OA. 在△OCA 和△ODB 中,{ 𝑂𝐶 = 𝑂𝐷, ∠𝐶𝑂𝐴 = ∠𝐷𝑂𝐵, 𝑂𝐴 = 𝑂𝐵, ∴△OCA≌△ODB(SAS), ∴∠OAC=∠OBD, 又∵∠ABC=∠BAD

∴.∠ABC+∠OBD=∠BAD+∠OAC, .∠ABD=∠BAC 18.解:(1)因为AF∥BC,所以∠AFE=∠DCE. 因为,点E为AD的中点,所以AE=DE. (LAFE=∠DCE, 在△AEF和△DEC中,{LAEF=LDEC, (AE=DE, 所以△AEF≌△DEC(AAS) (2)由(1)知△AEF≌△DEC, 所以FA=CD. 因为D是BC的中点,所以BD=CD, 所以AF=BD 因为AF∥BC,所以∠BAF=∠ABD (AF=BD. 在△ABF和△BAD中,LBAF=LABD, AB=BA. 所以△ABF≌△BAD(SAS),所以BF=AD. 19.解:(1),AD⊥BC,∠B=∠C=45° .∠B=∠FAD=45°. .DE⊥DF,∠BDE+∠EDA=90°,∠EDA+∠ADF=90°, ∴.∠BDE=∠ADF (∠B=∠FAD, 在△BDE和△ADF中,{BD=AD, ∠BDE=LADF, .△BDE≌△ADF(ASA) ∴.BE=AF (2)BE=AF.理由如下 如图,,∠ABD=∠DAC=45° ∴.∠EBD=∠FAD=135° :∠EDB+∠BDF=90°,∠BDF+∠FDA=90°, ∴.∠EDB=∠FDA (∠EBD=∠FAD, 在△EDB和△FDA中,{BD=AD, ∠EDB=∠FDA, ∴.△EDB≌△FDA(ASA). ∴.BE=AF
∴∠ABC+∠OBD=∠BAD+∠OAC, ∴∠ABD=∠BAC. 18.解:(1)因为 AF∥BC,所以∠AFE=∠DCE. 因为点 E 为 AD 的中点,所以 AE=DE. 在△AEF 和△DEC 中,{ ∠𝐴𝐹𝐸 = ∠𝐷𝐶𝐸, ∠𝐴𝐸𝐹 = ∠𝐷𝐸𝐶, 𝐴𝐸 = 𝐷𝐸, 所以△AEF≌△DEC(AAS). (2)由(1)知△AEF≌△DEC, 所以 FA=CD. 因为 D 是 BC 的中点,所以 BD=CD, 所以 AF=BD. 因为 AF∥BC,所以∠BAF=∠ABD. 在△ABF 和△BAD 中,{ 𝐴𝐹 = 𝐵𝐷, ∠𝐵𝐴𝐹 = ∠𝐴𝐵𝐷, 𝐴𝐵 = 𝐵𝐴, 所以△ABF≌△BAD(SAS),所以 BF=AD. 19.解:(1)∵AD⊥BC,∠B=∠C=45°. ∴∠B=∠FAD=45°. ∵DE⊥DF,∠BDE+∠EDA=90°,∠EDA+∠ADF=90°, ∴∠BDE=∠ADF. 在△BDE 和△ADF 中,{ ∠𝐵 = ∠𝐹𝐴𝐷, 𝐵𝐷 = 𝐴𝐷, ∠𝐵𝐷𝐸 = ∠𝐴𝐷𝐹, ∴△BDE≌△ADF(ASA). ∴BE=AF. (2)BE=AF.理由如下: 如图,∵∠ABD=∠DAC=45°, ∴∠EBD=∠FAD=135°. ∵∠EDB+∠BDF=90°,∠BDF+∠FDA=90°, ∴∠EDB=∠FDA. 在△EDB 和△FDA 中,{ ∠𝐸𝐵𝐷 = ∠𝐹𝐴𝐷, 𝐵𝐷 = 𝐴𝐷, ∠𝐸𝐷𝐵 = ∠𝐹𝐷𝐴, ∴△EDB≌△FDA(ASA). ∴BE=AF