
第二章检测 一、选择题(每小题4分,共32分) 1.如图,因为AB⊥I,BC⊥1,B为垂足,所以AB和BC重合,其理由是() A.两点确定一条直线 B.在同一平面内,过一点有且只有一条直线与己知直线垂直 C过一点能作一条垂线 D垂线段最短 2.如图,直线AB,CD相交于点O,且∠AOC+∠BOD=120°,则∠AOD的度数为 () A.130° B.120° C.110° D.100° 3.在同一平面内有四条直线,若满足aLb,b⊥c,c⊥d,则下列结论成立的是(). A.a∥d B.b⊥d C.a∥c D.b∥c 4.已知一副三角尺按如图所示的方式摆放,且∠1比∠2大50°,则∠2的度数为 () A.20° B.50° C.70 D.30 5.如图,AB∥CD,EF⊥CD于点F.若∠BEF=150°,则∠ABE=() A B E -D A.30° B.40° C.50 D.60° 6.如图,已知AB∥CD,直线AC和BD相交于点E若∠ABE=70°,∠ACD=40°,则 ∠AEB等于(
第二章检测 一、选择题(每小题 4 分,共 32 分) 1.如图,因为 AB⊥l,BC⊥l,B 为垂足,所以 AB 和 BC 重合,其理由是( ). A.两点确定一条直线 B.在同一平面内,过一点有且只有一条直线与已知直线垂直 C.过一点能作一条垂线 D.垂线段最短 2.如图,直线 AB,CD 相交于点 O,且∠AOC+∠BOD=120°,则∠AOD 的度数为 ( ). A.130° B.120° C.110° D.100° 3.在同一平面内有四条直线,若满足 a⊥b,b⊥c,c⊥d,则下列结论成立的是( ). A.a∥d B.b⊥d C.a∥c D.b∥c 4.已知一副三角尺按如图所示的方式摆放,且∠1 比∠2 大 50°,则∠2 的度数为 ( ). A.20° B.50° C.70° D.30° 5.如图,AB∥CD,EF⊥CD 于点 F.若∠BEF=150°,则∠ABE=( ). A.30° B.40° C.50° D.60° 6.如图,已知 AB∥CD,直线 AC 和 BD 相交于点 E.若∠ABE=70°,∠ACD=40°,则 ∠AEB 等于( )

A.50° B.60° C.70 D.80 7.如图,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD:∠BOE =4:1,则∠AOF等于() A.130° B.120° C.110° D.100° 8.如图,如果∠1=∠2,DE∥BC,那么下列结论中正确的个数为() ①FG∥DC,②∠AED=∠ACB:③CD平分∠ACB:④∠1+∠B=90°:⑤∠BFG=∠ BDC. A.1 B.2 C.3 D.4 二、填空题(每小题4分,共24分) 9.(2022贵州毕节模拟)若两个互补的角的度数之比为1:2,则这两个角中较小角 的度数是 10.已知两条直线相交所成的四个角中,有两个角分别是(2x-10)°和(110-x)°,则 x= 11.已知两条直线被第三条直线所截,∠2是∠3的同旁内角,∠1是∠3的内错角. 若∠2=4∠3,∠3=2∠1,则∠1的度数是 12.如图,AB∥CD,AC∥BD,∠1=28°,则∠2的度数为 A D C文2 13.如图,AB∥EF,∠ABC=75°,∠CDF=135°,则∠BCD= A B E D 135° 14.一副直角三角尺如图①所示叠放,现将含有45°角的三角尺ADE固定不动,将 含有30°角的三角尺ABC绕顶点A顺时针转动(旋转角不超过180°),使两个三
A.50° B.60° C.70° D.80° 7.如图,直线 AB 交 CD 于点 O,OE 平分∠BOD,OF 平分∠COB,∠AOD∶∠BOE =4∶1,则∠AOF 等于( ). A.130° B.120° C.110° D.100° 8.如图,如果∠1=∠2,DE∥BC,那么下列结论中正确的个数为( ). ①FG∥DC;②∠AED=∠ACB;③CD 平分∠ACB;④∠1+∠B=90°;⑤∠BFG=∠ BDC. A.1 B.2 C.3 D.4 二、填空题(每小题 4 分,共 24 分) 9.(2022·贵州毕节模拟)若两个互补的角的度数之比为 1∶2,则这两个角中较小角 的度数是 . 10.已知两条直线相交所成的四个角中,有两个角分别是(2x-10)°和(110-x)°,则 x= . 11.已知两条直线被第三条直线所截,∠2 是∠3 的同旁内角,∠1 是∠3 的内错角. 若∠2=4∠3,∠3=2∠1,则∠1 的度数是 . 12.如图,AB∥CD,AC∥BD,∠1=28°,则∠2 的度数为 . 13.如图,AB∥EF,∠ABC=75°,∠CDF=135°,则∠BCD= . 14.一副直角三角尺如图①所示叠放,现将含有 45°角的三角尺 ADE 固定不动,将 含有 30°角的三角尺 ABC 绕顶点 A 顺时针转动(旋转角不超过 180°),使两个三
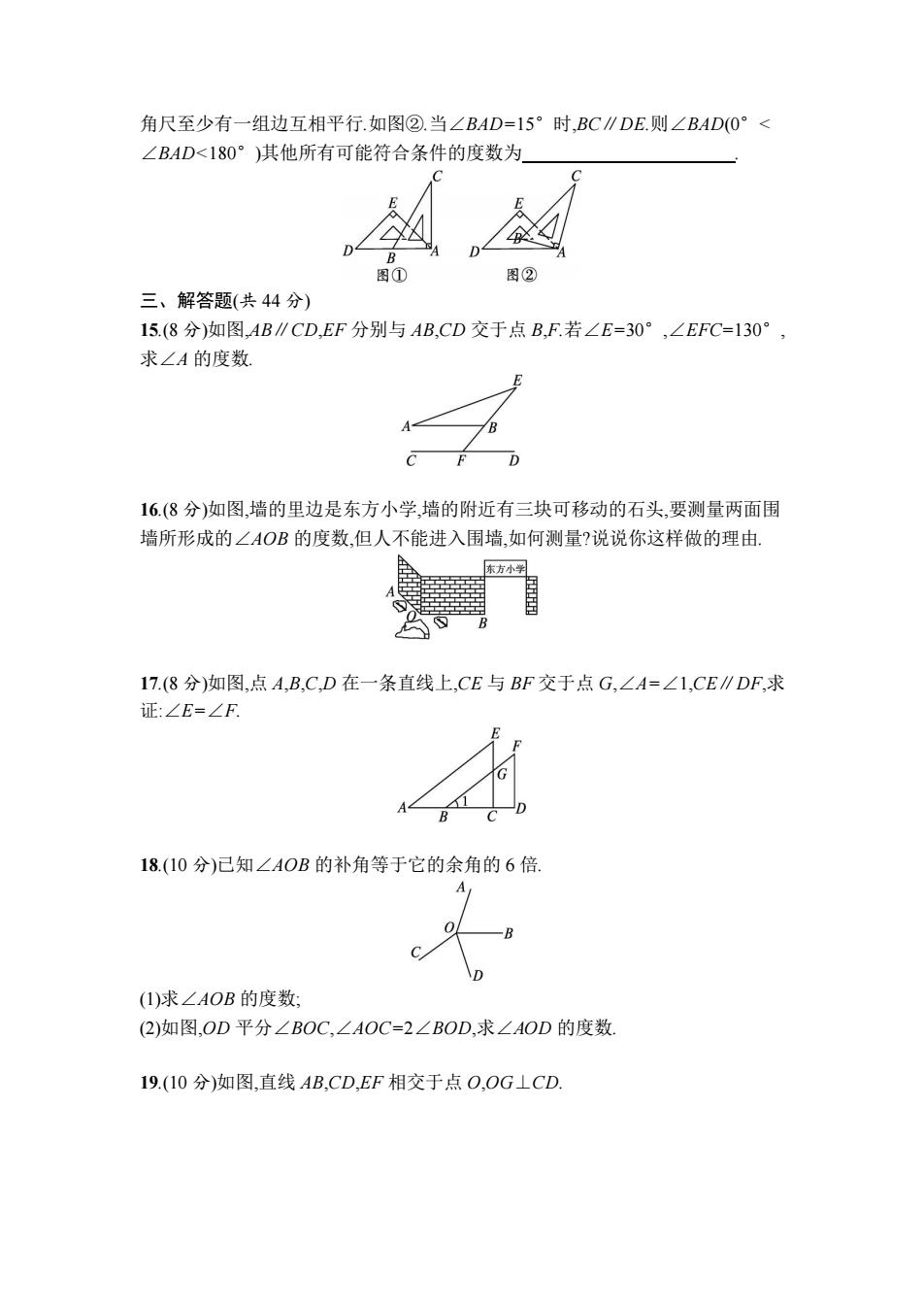
角尺至少有一组边互相平行.如图②.当∠BAD=15°时,BC∥DE.则∠BAD(0°< ∠BAD<180°)其他所有可能符合条件的度数为 图① 图② 三、解答题(共44分) 15.(8分)如图,AB∥CD,EF分别与AB,CD交于点B,F.若∠E=30°,∠EFC=130°, 求∠A的度数. 16.(8分)如图,墙的里边是东方小学,墙的附近有三块可移动的石头,要测量两面围 墙所形成的∠AOB的度数,但人不能进入围墙,如何测量?说说你这样做的理由. 东方小学 17.(8分)如图,点A,B,C,D在一条直线上,CE与BF交于点G,∠A=∠1,CE∥DF,求 证:∠E=∠F. 1 D B 18.(10分)已知∠AOB的补角等于它的余角的6倍. (1)求∠AOB的度数: (2)如图,OD平分∠BOC,∠AOC=2∠BOD,求∠AOD的度数. 19.(10分)如图,直线AB,CD,EF相交于点O,OG⊥CD
角尺至少有一组边互相平行.如图②.当∠BAD=15°时,BC∥DE.则∠BAD(0°< ∠BAD<180°)其他所有可能符合条件的度数为 . 三、解答题(共 44 分) 15.(8 分)如图,AB∥CD,EF 分别与 AB,CD 交于点 B,F.若∠E=30°,∠EFC=130°, 求∠A 的度数. 16.(8 分)如图,墙的里边是东方小学,墙的附近有三块可移动的石头,要测量两面围 墙所形成的∠AOB 的度数,但人不能进入围墙,如何测量?说说你这样做的理由. 17.(8 分)如图,点 A,B,C,D 在一条直线上,CE 与 BF 交于点 G,∠A=∠1,CE∥DF,求 证:∠E=∠F. 18.(10 分)已知∠AOB 的补角等于它的余角的 6 倍. (1)求∠AOB 的度数; (2)如图,OD 平分∠BOC,∠AOC=2∠BOD,求∠AOD 的度数. 19.(10 分)如图,直线 AB,CD,EF 相交于点 O,OG⊥CD

(1)已知∠BOD=36°,求∠AOG的度数: (2)如果OC是∠AOE的平分线,那么OG是∠AOF的平分线吗?说明理由: 答案: 一、选择题 1.B2.B3.C4.A5.D6.C7.B8.C 二、填空题 9.60°10.40或8011.20°12.28°13.30°14.45°,60°,105°,135° 三、解答题 15.解:.AB∥CD,∴.∠ABE=∠CFB=130°, 又∠E=30°, ∴.∠A=180°-∠E-∠ABE=180°-30°-130°=20° 16.解:如图,在墙角的远处选一点D,使点D,O,B在同一条直线上,然后将铁丝的一 端固定在D处,沿着直线DB的方向拉直,到,点M处,再转动拉直,使PM与OA平 行,得到∠PMD,所量出∠PMD的度数就是墙的夹角∠AOB的度数了. 东方小学 理由:两直线平行,同位角相等 17.证明,CE∥DF,∴.∠ACE=∠D .∠A=∠1 ∴.180°-∠ACE-∠A=180°-∠D-∠1, 又.∠E=180°-∠ACE-∠A,∠F=180°-∠D-∠1, ∴.∠E=∠F 18.解:(1)设∠AOB的度数为x 由题意,得180-x=6(90-x),解得x=72° .∠AOB的度数为72° (2)设∠BOD的度数为y, .OD平分∠BOC,∴.∠BOC=2y ,∠AOC=2∠BOD, ∴.∠AOC=∠BOC=2y .2y+2y+72°=360°,解得y=72° ∴.∠AOD=∠AOB+∠BOD=144°. 19.解:(1).AB,CD相交于点O
(1)已知∠BOD=36°,求∠AOG 的度数; (2)如果 OC 是∠AOE 的平分线,那么 OG 是∠AOF 的平分线吗?说明理由. 答案: 一、选择题 1.B 2.B 3.C 4.A 5.D 6.C 7.B 8.C 二、填空题 9.60° 10.40 或 80 11.20° 12.28° 13.30° 14.45°,60°,105°,135° 三、解答题 15.解:∵AB∥CD,∴∠ABE=∠CFB=130°, 又∠E=30°, ∴∠A=180°-∠E-∠ABE=180°-30°-130°=20°. 16.解:如图,在墙角的远处选一点 D,使点 D,O,B 在同一条直线上,然后将铁丝的一 端固定在 D 处,沿着直线 DB 的方向拉直,到点 M 处,再转动拉直,使 PM 与 OA 平 行,得到∠PMD,所量出∠PMD 的度数就是墙的夹角∠AOB 的度数了. 理由:两直线平行,同位角相等. 17.证明 ∵CE∥DF,∴∠ACE=∠D, ∵∠A=∠1, ∴180°-∠ACE-∠A=180°-∠D-∠1, 又∵∠E=180°-∠ACE-∠A,∠F=180°-∠D-∠1, ∴∠E=∠F. 18.解:(1)设∠AOB 的度数为 x. 由题意,得 180-x=6(90-x),解得 x=72°. ∴∠AOB 的度数为 72°. (2)设∠BOD 的度数为 y, ∵OD 平分∠BOC,∴∠BOC=2y. ∵∠AOC=2∠BOD, ∴∠AOC=∠BOC=2y. ∴2y+2y+72°=360°,解得 y=72°. ∴∠AOD=∠AOB+∠BOD=144°. 19.解:(1)∵AB,CD 相交于点 O

.∠AOC=∠BOD..∠BOD=36°, ∴.∠AOC=∠BOD=36° .OG⊥CD,∴.∠COG=90° 即∠AOC+∠AOG=90°, .∠A0G=90°-∠A0C=90°-36°=54°. (2).OC平分∠AOE, ∴.∠AOC=∠COE. .∠C0G=90°,.∠AOC+∠AOG=90°. ,∠COE+∠AOC+∠AOG+∠GOF=180°, ∴.∠COE+∠GOF=90°. ∴.∠AOG=∠GOF 即OG是∠AOF的平分线
∴∠AOC=∠BOD.∵∠BOD=36°, ∴∠AOC=∠BOD=36°. ∵OG⊥CD,∴∠COG=90°, 即∠AOC+∠AOG=90°, ∴∠AOG=90°-∠AOC=90°-36°=54°. (2)∵OC 平分∠AOE, ∴∠AOC=∠COE. ∵∠COG=90°,∴∠AOC+∠AOG=90°. ∵∠COE+∠AOC+∠AOG+∠GOF=180°, ∴∠COE+∠GOF=90°. ∴∠AOG=∠GOF, 即 OG 是∠AOF 的平分线