
第四章检测 一、选择题(每小题3分,共30分) 1.下列关于棱柱的说法:①棱柱的所有面都是平面:②棱柱的所有棱长都相等:③棱 柱的所有侧面都完全一样,④棱柱的侧面个数与底面边数相等:⑤棱柱的上下底面 形状相同、大小相等.其中正确的有(B)】 A.2个 B.3个 C.4个 D.5个 2.下列说法正确的是(B), A.直线AB和直线BA是两条直线 B.射线AB和射线BA是两条射线 C.线段AB和线段BA是两条线段 D.直线AB和直线a不能是同一条直线 3.如图,C是线段AB的中点,D是线段BC的中点,下列等式错误的是(D) C D B A.CD=AC-DB B.CD=AD-BC C.CD-AB-BD D.CD-AB 4.如图,若∠BOD=2∠AOB,OC是∠AOD的平分线,则下列结论: ①∠BOC-∠AOB:②∠D0C=2∠BOC,③∠COB-∠AOB,④∠COD=3∠BOC 其中正确的是(B), A.①②B.③④
第四章检测 一、选择题(每小题 3 分,共 30 分) 1.下列关于棱柱的说法:①棱柱的所有面都是平面;②棱柱的所有棱长都相等;③棱 柱的所有侧面都完全一样;④棱柱的侧面个数与底面边数相等;⑤棱柱的上下底面 形状相同、大小相等.其中正确的有(B). A.2 个 B.3 个 C.4 个 D.5 个 2.下列说法正确的是(B). A.直线 AB 和直线 BA 是两条直线 B.射线 AB 和射线 BA 是两条射线 C.线段 AB 和线段 BA 是两条线段 D.直线 AB 和直线 a 不能是同一条直线 3.如图,C 是线段 AB 的中点,D 是线段 BC 的中点,下列等式错误的是(D). A.CD=AC-DB B.CD=AD-BC C.CD=1 2 AB-BD D.CD=1 3 AB 4.如图,若∠BOD=2∠AOB,OC 是∠AOD 的平分线,则下列结论: ①∠BOC=1 3 ∠AOB;②∠DOC=2∠BOC;③∠COB=1 2 ∠AOB;④∠COD=3∠BOC. 其中正确的是(B). A.①② B.③④

C.②③D.①④ 5.已知某手提水果篮抽象的立体图形如图所示,则从上面看它得到的平面图形为 (A) B D 6.己知M,N,P,Q四点的位置如图所示,点O在直线MN上,下列结论中,正确的是 (C) A.∠NOQ与∠NOP互补 B.∠NOP与∠MOQ互余 C.∠PON比∠MOQ小 D.∠MOQ与∠MOP互补 7.要在一条直线上得到10条不同的线段,那么在这条直线上至少要选用(D) A.20个点 B.10个点 C.7个点 D.5个点 8.如图,∠1=25°,∠AOC=90°,B,O,D三点共线,则∠1的余角的补角∠3的度数是 (B) D A.65° B.115 C.25°
C.②③ D.①④ 5.已知某手提水果篮抽象的立体图形如图所示,则从上面看它得到的平面图形为 (A). A B C D 6.已知 M,N,P,Q 四点的位置如图所示,点 O 在直线 MN 上,下列结论中,正确的是 (C). A.∠NOQ 与∠NOP 互补 B.∠NOP 与∠MOQ 互余 C.∠PON 比∠MOQ 小 D.∠MOQ 与∠MOP 互补 7.要在一条直线上得到 10 条不同的线段,那么在这条直线上至少要选用(D). A.20 个点 B.10 个点 C.7 个点 D.5 个点 8.如图,∠1=25°,∠AOC=90°,B,O,D 三点共线,则∠1 的余角的补角∠3 的度数是 (B). A.65° B.115° C.25°
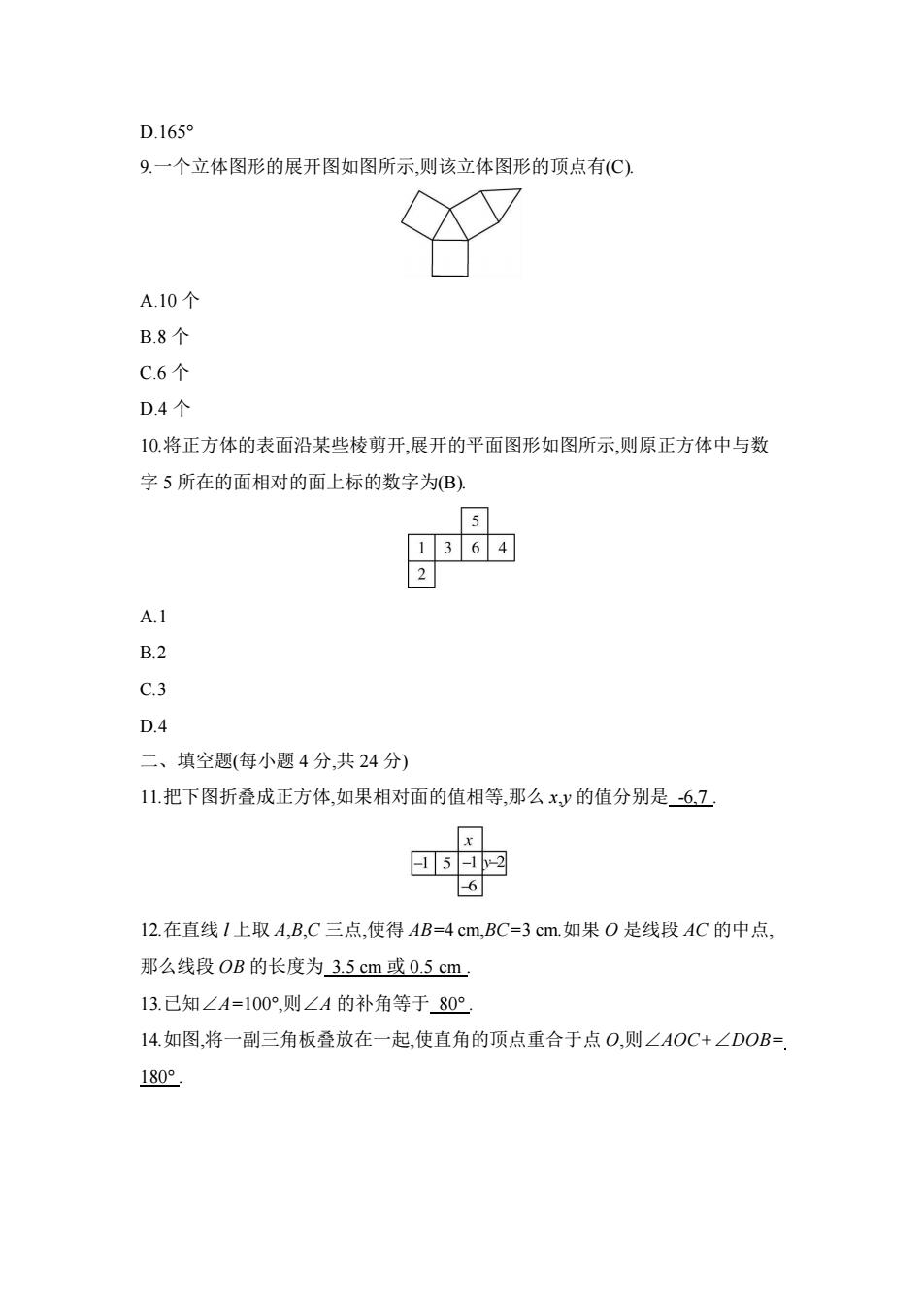
D.1659 9.一个立体图形的展开图如图所示,则该立体图形的顶点有(C) A.10个 B.8个 C.6个 D.4个 10.将正方体的表面沿某些棱剪开,展开的平面图形如图所示,则原正方体中与数 字5所在的面相对的面上标的数字为(B), 5 6 4 2 A.1 B.2 C.3 D.4 二、填空题(每小题4分,共24分) 11.把下图折叠成正方体,如果相对面的值相等,那么x,y的值分别是-67 5-1-2 6 12.在直线1上取A,B,C三点,使得AB=4cm,BC=-3cm.如果O是线段AC的中点, 那么线段OB的长度为3.5cm或0.5cm 13.已知∠A=100°,则∠A的补角等于80° 14.如图,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOC+∠DOB= 180°
D.165° 9.一个立体图形的展开图如图所示,则该立体图形的顶点有(C). A.10 个 B.8 个 C.6 个 D.4 个 10.将正方体的表面沿某些棱剪开,展开的平面图形如图所示,则原正方体中与数 字 5 所在的面相对的面上标的数字为(B). A.1 B.2 C.3 D.4 二、填空题(每小题 4 分,共 24 分) 11.把下图折叠成正方体,如果相对面的值相等,那么 x,y 的值分别是 -6,7 . 12.在直线 l 上取 A,B,C 三点,使得 AB=4 cm,BC=3 cm.如果 O 是线段 AC 的中点, 那么线段 OB 的长度为 3.5 cm 或 0.5 cm . 13.已知∠A=100°,则∠A 的补角等于 80° . 14.如图,将一副三角板叠放在一起,使直角的顶点重合于点 O,则∠AOC+∠DOB= 180°

15.如果乘火车从A站出发,沿途经过2个车站可到达B站,那么在A,B两站之间 共有12种不同的车票 16.一块手表,早上8时的时针、分针的位置如图所示,分针与时针所成的角的度数 是120° 三、解答题(共96分,写出必要的文字说明、证明过程或演算步骤) 17.(6分)如图,两个几何体由几个面围成?面与面相交成几条线?它们是直的还是 曲的? ② 答案:图中的几何体①油4个面围成,面与面相交成6条线,这些线中有4条直的(线 段),还有2条曲的(半圆)几何体②油7个面围成,面与面相交成14条线,这些线全 部都是直的(线段), 18.(6分)按下列要求画出图形 (1)射线AB外有一点C (2)直线1经过点A,B,点P不在直线1上 (3)直线AB,BC相交于点B,以点B为端点有一条线段BN (4)线段a与b相交于点A. 答案:如图 (1)
15.如果乘火车从 A 站出发,沿途经过 2 个车站可到达 B 站,那么在 A,B 两站之间 共有 12 种不同的车票. 16.一块手表,早上 8 时的时针、分针的位置如图所示,分针与时针所成的角的度数 是 120° . 三、解答题(共 96 分,写出必要的文字说明、证明过程或演算步骤) 17.(6 分)如图,两个几何体由几个面围成?面与面相交成几条线?它们是直的还是 曲的? 答案:图中的几何体①由4个面围成,面与面相交成 6条线,这些线中有 4条直的(线 段),还有 2 条曲的(半圆).几何体②由 7 个面围成,面与面相交成 14 条线,这些线全 部都是直的(线段). 18.(6 分)按下列要求画出图形. (1)射线 AB 外有一点 C. (2)直线 l 经过点 A,B,点 P 不在直线 l 上. (3)直线 AB,BC 相交于点 B,以点 B 为端点有一条线段 BN. (4)线段 a 与 b 相交于点 A. 答案:如图. (1)
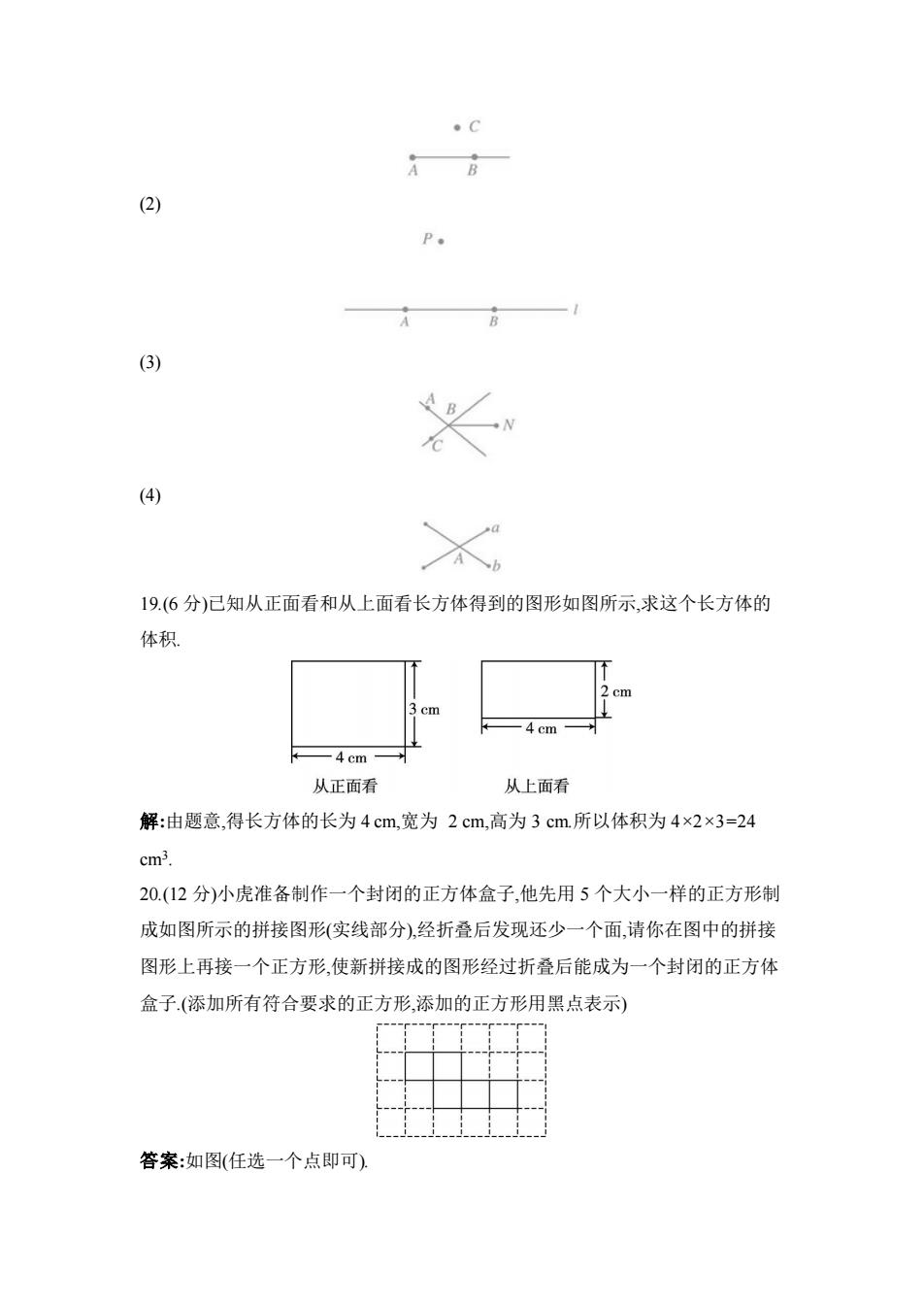
(2) (3) (4) 19.(6分)已知从正面看和从上面看长方体得到的图形如图所示,求这个长方体的 体积 cm cm 4 cm 4 cm 从正面看 从上面看 解:由题意,得长方体的长为4cm,宽为2cm,高为3cm.所以体积为4×2×3=24 cm3 20.(12分)小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制 成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在图中的拼接 图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体 盒子.(添加所有符合要求的正方形,添加的正方形用黑点表示) 答案:如图(任选一个点即可)
(2) (3) (4) 19.(6 分)已知从正面看和从上面看长方体得到的图形如图所示,求这个长方体的 体积. 解:由题意,得长方体的长为 4 cm,宽为 2 cm,高为 3 cm.所以体积为 4×2×3=24 cm3 . 20.(12 分)小虎准备制作一个封闭的正方体盒子,他先用 5 个大小一样的正方形制 成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在图中的拼接 图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体 盒子.(添加所有符合要求的正方形,添加的正方形用黑点表示) 答案:如图(任选一个点即可)
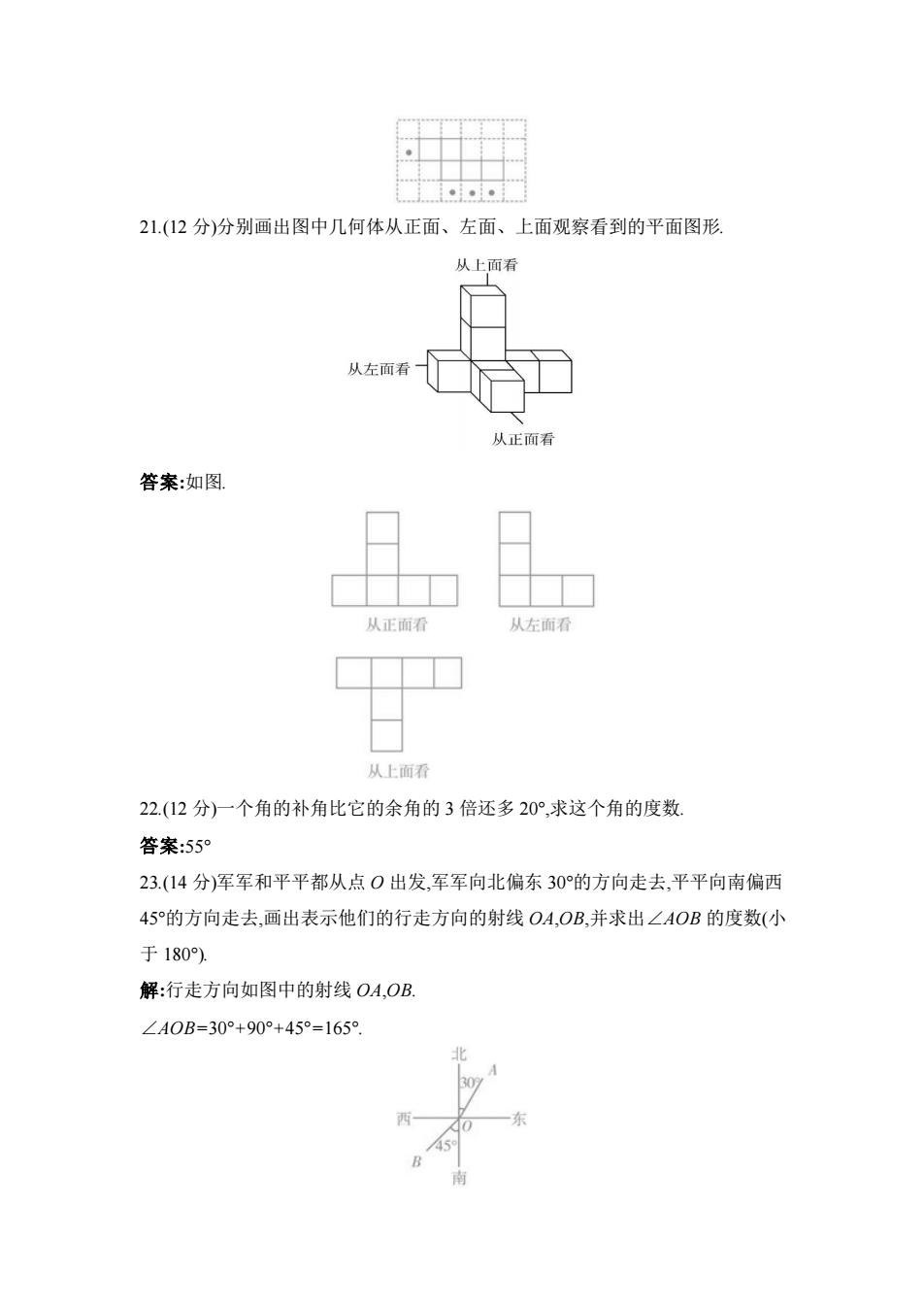
21.(12分)分别画出图中几何体从正面、左面、上面观察看到的平面图形 从上面看 从左面看 从正面看 答案:如图。 从正面看 从左面看 从上面看 22.(12分)一个角的补角比它的余角的3倍还多20°,求这个角的度数 答案:55 23.(14分)军军和平平都从点0出发,军军向北偏东30°的方向走去,平平向南偏西 45的方向走去,画出表示他们的行走方向的射线OA,OB,并求出∠AOB的度数(小 于180). 解:行走方向如图中的射线OA,OB ∠AOB=30°+90°+45°=165° 30 1 南
21.(12 分)分别画出图中几何体从正面、左面、上面观察看到的平面图形. 答案:如图. 22.(12 分)一个角的补角比它的余角的 3 倍还多 20°,求这个角的度数. 答案:55° 23.(14 分)军军和平平都从点 O 出发,军军向北偏东 30°的方向走去,平平向南偏西 45°的方向走去,画出表示他们的行走方向的射线 OA,OB,并求出∠AOB 的度数(小 于 180°). 解:行走方向如图中的射线 OA,OB. ∠AOB=30°+90°+45°=165°

24.(14分)如图,线段AD=10cm,线段AC=BD=7cm,E,F分别是线段AB,CD的中点. 求EF的长 A E B CF D 答案:7cm 25.(14分)如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC (1)求∠MON的度数 (2)如果已知∠AOB=80°,其他条件不变,求∠MON的度数. (3)如果已知∠BOC=60°,其他条件不变,求∠MON的度数. (4)从(1)2)3)中你能得出什么规律? 解(1)因为OM平分∠AOC, 所以∠MOC=2∠AOC. 又ON平分∠BOC, 所以∠NOC-=号∠BOC. 所以∠MON=∠MOC-∠NOC-号∠AOC∠BOC=号∠AOB 而∠AOB=90°,所以∠MON=45° (2)当∠AOB=80°,其他条件不变时, ∠M0N=2×80°=40°, (3)当∠BOC=60°,其他条件不变时, ∠MON=45°. (4)分析(1)2)(3)的结果和(1)的解题过程可知:∠MON-三∠AOB,∠MON的大小与 ∠BOC的大小无关
24.(14 分)如图,线段 AD=10 cm,线段 AC=BD=7 cm,E,F 分别是线段AB,CD 的中点. 求 EF 的长. 答案:7 cm 25.(14 分)如图,已知∠AOB=90°,∠BOC=30°,OM 平分∠AOC,ON 平分∠BOC. (1)求∠MON 的度数. (2)如果已知∠AOB=80°,其他条件不变,求∠MON 的度数. (3)如果已知∠BOC=60°,其他条件不变,求∠MON 的度数. (4)从(1)(2)(3)中你能得出什么规律? 解:(1)因为 OM 平分∠AOC, 所以∠MOC=1 2 ∠AOC. 又 ON 平分∠BOC, 所以∠NOC=1 2 ∠BOC. 所以∠MON=∠MOC-∠NOC=1 2 ∠AOC- 1 2 ∠BOC=1 2 ∠AOB. 而∠AOB=90°,所以∠MON=45°. (2)当∠AOB=80°,其他条件不变时, ∠MON=1 2 ×80°=40°. (3)当∠BOC=60°,其他条件不变时, ∠MON=45°. (4)分析(1)(2)(3)的结果和(1)的解题过程可知:∠MON=1 2 ∠AOB,∠MON 的大小与 ∠BOC 的大小无关