
期中检测 一、选择题(每小题4分,共40分) 1.3的相反数是( A.-3 B.3 c D号 2.2019年6月5日,长征十一号运载火箭成功完成了“一箭七星”海上发射技术试验,该火箭重 58000kg将数据58000用科学记数法表示为(). A.58×103 B.5.8×10 C.0.58×105 D.5.8×104 3.在数轴上,点A,B在原点O的两侧,分别表示数α,2,将点A向右平移1个单位长度,得到点 C,若CO=BO,则a的值为( A.-3 B.-2 C.-1 D.1 4.多项式1+)2的次数及最高次项的系数分别是( A.2,1 B.2,-1 C.3,-1 D.5,-1 m个2 52x2Xx2 3+3+…+3 n个3 A婴 B.2m 3n C.m D 6.下列说法:①柱体的两个底面一样大:②圆柱、圆锥的底面都是圆:③棱柱的底面是四边形 ④棱柱的顶点数一定是偶数,棱的条数一定是3的倍数;⑤棱柱的侧面形状都是平行四边形, 其中正确的个数是() A.2 B.3 C.4 D.5 7.有理数a,b,c,d在数轴上的位置如图所示,下列关系式不正确的是(). a b 0 1 c A.lal>b B.ac=ac C.b0 8.若a-b=2,b-c=-3,则a-c等于( ). A.1 B.-1 C.5 D.-5 9已知有理数1,我们把品称为a的差倒数如2的差倒数是之-1,1的差倒数是高=号 如果a1=-2,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数…依此类推,那么 a1+a2+…+a1o0的值是(). A.-7.5 B.7.5 C.5.5 D.-5.5 10.骰子是6个面上分别写有数字1,2,3,4,5,6的小立方体,它任意两个对面上所写的两个数字 之和为7将相同的几个骰子按照相接触的两个面上的数字的积为6的规律摆成一个几何体, 这个几何体从三个方向看到的形状图如图所示已知图中所标注的是部分面上的数字,则“※” 所代表的数字是( 从正面看 从左面看 从上面看 A.4 B.5 C.2 D.6 二、填空题(每小题4分,共24分) 11.请举一个能说明“面动成体的生活现象 12.已知代数式23c是7次单项式,则m的值是」 3 13.已知2a-3b=7,则8+6b-4a= 14.若a2=4,b=3且a>b,则ab= 15.规定一种新的运算:a△b=Qb-a+b+1.如3△4=3×4-3+4+1=12-3+4+1=14.比较大小:(-3)△4 4△(-3).(填>%-”或<
期中检测 一、选择题(每小题 4 分,共 40 分) 1.3 的相反数是( ). A.-3 B.3 C.- 1 3 D. 1 3 2.2019 年 6 月 5 日,长征十一号运载火箭成功完成了“一箭七星”海上发射技术试验,该火箭重 58 000 kg,将数据 58 000 用科学记数法表示为( ). A.58×103 B.5.8×103 C.0.58×105 D.5.8×104 3.在数轴上,点 A,B 在原点 O 的两侧,分别表示数 a,2,将点 A 向右平移 1 个单位长度,得到点 C,若 CO=BO,则 a 的值为( ). A.-3 B.-2 C.-1 D.1 4.多项式 1+xy-xy2 的次数及最高次项的系数分别是( ). A.2,1 B.2,-1 C.3,-1 D.5,-1 5. 2⏞×2×…×2 𝑚个 2 3⏟+ 3 + … + 3 n 个 3 =( ). A. 2𝑚 3 𝑛 B. 2 𝑚 3𝑛 C. 2𝑚 𝑛 3 D. 𝑚2 3𝑛 6.下列说法:①柱体的两个底面一样大;②圆柱、圆锥的底面都是圆;③棱柱的底面是四边形; ④棱柱的顶点数一定是偶数,棱的条数一定是 3 的倍数;⑤棱柱的侧面形状都是平行四边形, 其中正确的个数是( ). A.2 B.3 C.4 D.5 7.有理数 a,b,c,d 在数轴上的位置如图所示,下列关系式不正确的是( ). A.|a|>|b| B.|ac|=ac C.b0 8.若 a-b=2,b-c=-3,则 a-c 等于( ). A.1 B.-1 C.5 D.-5 9.已知有理数 a≠1,我们把 1 1-𝑎称为 a 的差倒数,如:2 的差倒数是 1 1-2 =-1,-1 的差倒数是 1 1-(-1) = 1 2 . 如果 a1=-2,a2 是 a1 的差倒数,a3 是 a2 的差倒数,a4 是 a3 的差倒数……依此类推,那么 a1+a2+…+a100 的值是( ). A.-7.5 B.7.5 C.5.5 D.-5.5 10.骰子是 6 个面上分别写有数字 1,2,3,4,5,6 的小立方体,它任意两个对面上所写的两个数字 之和为 7.将相同的几个骰子按照相接触的两个面上的数字的积为 6 的规律摆成一个几何体, 这个几何体从三个方向看到的形状图如图所示.已知图中所标注的是部分面上的数字,则“※” 所代表的数字是( ). A.4 B.5 C.2 D.6 二、填空题(每小题 4 分,共 24 分) 11.请举一个能说明“面动成体”的生活现象: . 12.已知代数式- 2 3 𝑎𝑚𝑏 3 𝑐 2 3 是 7 次单项式,则 m 的值是 . 13.已知 2a-3b=7,则 8+6b-4a= . 14.若 a 2=4,|b|=3 且 a>b,则 a·b= . 15.规定一种新的运算:a△b=a·b-a+b+1.如 3△4=3×4-3+4+1=12-3+4+1=14.比较大小:(-3)△4 4△(-3).(填“>”“=”或“<”)
16.如图,电视台的摄像机1~4号在不同位置拍摄了四幅画面,则A图象是 号摄像 机所拍,B图象是 号摄像机所拍,C图象是 号摄像机所拍,D图象是■ 号摄像机所拍 B D 三、解答题(共56分) 17.(9分)计算与化简 (+君)-() (2-2+(-24)-43×(} (3)3(a2-4a+3)-5(52-a+2). 18.(7分)己知a是绝对值等于2的负数,b是最小的正整数,c的倒数的相反数是-2,求代数式 4a2b3-[2abc+(5a2b3.-7abc)-a2b]的值. 19.(9分)如图,将边长为m的正方形纸板沿虚线剪成两个小正方形和两个长方形,拿掉边长为 n的小正方形纸板后,将剩下的三块拼成新的长方形. (I)用含m或n的整式表示拼成的长方形的周长, (2)若m=7,n=4,求拼成的长方形的面积 20.(9分)由一些大小相同的小立方块搭成一个简单的几何体,分别从正面与上面看到的形状 图如图所示
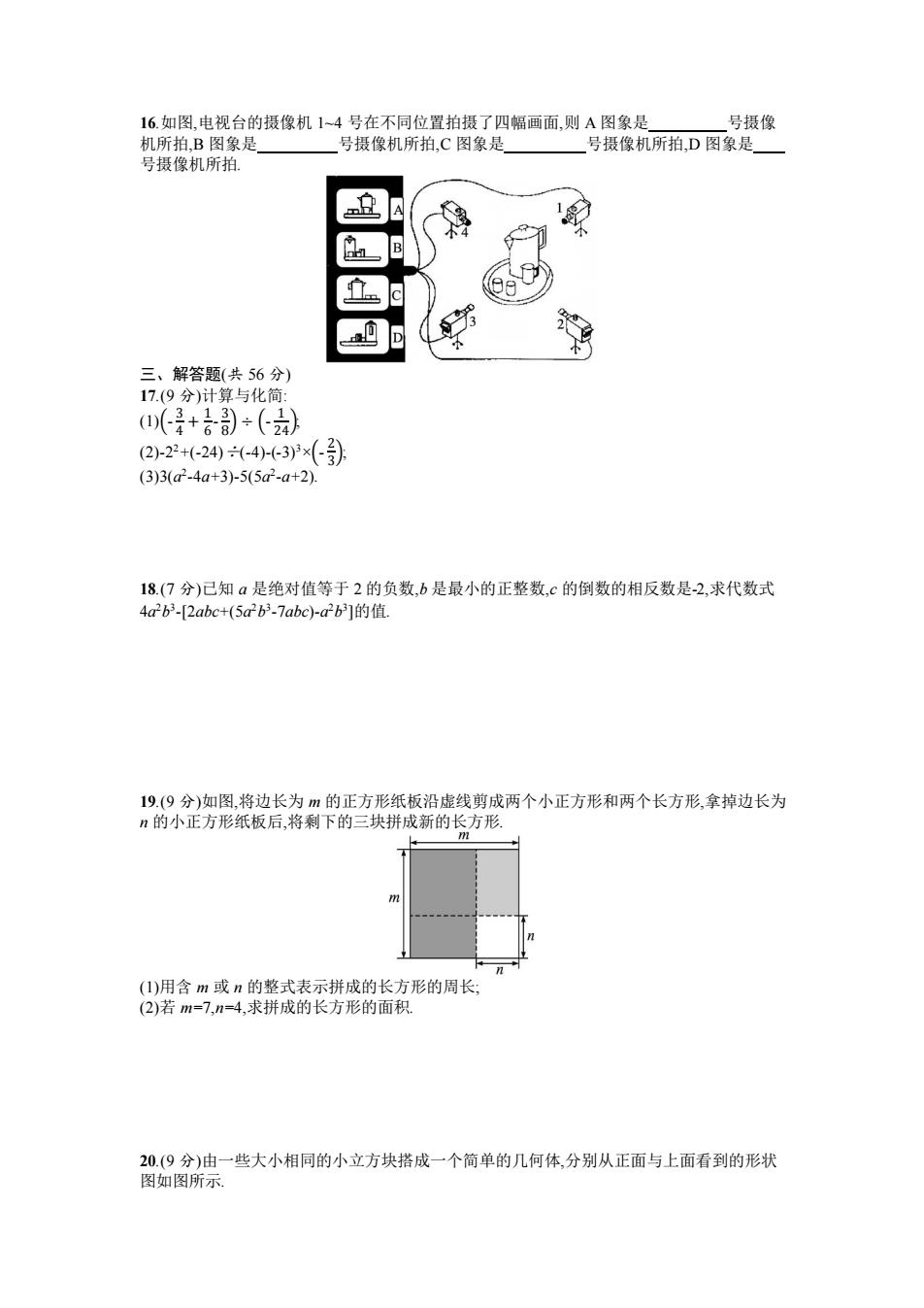
16.如图,电视台的摄像机 1~4 号在不同位置拍摄了四幅画面,则 A 图象是 号摄像 机所拍,B 图象是 号摄像机所拍,C 图象是 号摄像机所拍,D 图象是 号摄像机所拍. 三、解答题(共 56 分) 17.(9 分)计算与化简: (1)(- 3 4 + 1 6 - 3 8 ) ÷ (- 1 24); (2)-2 2+(-24)÷(-4)-(-3)3×(- 2 3 ); (3)3(a 2 -4a+3)-5(5a 2 -a+2). 18.(7 分)已知 a 是绝对值等于 2 的负数,b 是最小的正整数,c 的倒数的相反数是-2,求代数式 4a 2b 3 -[2abc+(5a 2b 3 -7abc)-a 2b 3 ]的值. 19.(9 分)如图,将边长为 m 的正方形纸板沿虚线剪成两个小正方形和两个长方形,拿掉边长为 n 的小正方形纸板后,将剩下的三块拼成新的长方形. (1)用含 m 或 n 的整式表示拼成的长方形的周长; (2)若 m=7,n=4,求拼成的长方形的面积. 20.(9 分)由一些大小相同的小立方块搭成一个简单的几何体,分别从正面与上面看到的形状 图如图所示

从正面看 从上面看 (1)请你画出从这个几何体左面看到的形状图: (2)若搭成这个几何体的小立方块的块数为n,请你写出n的所有可能值 21.(10分)国庆黄金周期间,某公园在7天中每天旅游的人数变化如下表(正数表示比前一天 多的人数,负数表示比前一天少的人数) 旧期10月1日 10月2日 10月3日 10月4日10月5日 10月6日10月7日 人数变 +1.6 +0.8 +0.4 -0.4 0.8 +0.2 化万人 1.2 (1)若9月30日的游客人数记为a,请用含a的代数式表示10月2日的游客人数.(3分) (2)请判断七天内游客人数最多的是哪天?并说明理由.(4分) (3)若9月30日的游客人数为2万人,门票每人50元,问这个公园在国庆黄金周期间门票收 入是多少万元?(3分) 22.(12分)大学生康康自主创业,开了一间咖啡馆,新网购的每一张正方形的桌子可坐4人,按 照如图的方式将桌子拼在一起,试回答下列问题 (1)两张桌子拼在一起可以坐几人?三张桌子拼在一起可以坐几人?张桌子拼在一起可以坐 几人? (2)咖啡馆里有60张这样的正方形桌子,按下图方式每4张拼成一个大桌子,则60张桌子可 以拼成15张大桌子,共可坐多少人? (3)在(2)中若每4张桌子拼成一个大的正方形,共可坐多少人? (4)对于咖啡馆,哪种拼桌子的方式可以坐的人更多? ●
(1)请你画出从这个几何体左面看到的形状图; (2)若搭成这个几何体的小立方块的块数为 n,请你写出 n 的所有可能值. 21.(10 分)国庆黄金周期间,某公园在 7 天中每天旅游的人数变化如下表(正数表示比前一天 多的人数,负数表示比前一天少的人数) 日期 10 月 1 日 10 月 2 日 10 月 3 日 10 月 4 日 10 月 5 日 10 月 6 日 10 月 7 日 人数变 化/万人+1.6 +0.8 +0.4 -0.4 -0.8 +0.2 -1.2 (1)若 9 月 30 日的游客人数记为 a,请用含 a 的代数式表示 10 月 2 日的游客人数.(3 分) (2)请判断七天内游客人数最多的是哪天?并说明理由.(4 分) (3)若 9 月 30 日的游客人数为 2 万人,门票每人 50 元,问这个公园在国庆黄金周期间门票收 入是多少万元?(3 分) 22.(12 分)大学生康康自主创业,开了一间咖啡馆,新网购的每一张正方形的桌子可坐 4 人,按 照如图的方式将桌子拼在一起,试回答下列问题. (1)两张桌子拼在一起可以坐几人?三张桌子拼在一起可以坐几人?n 张桌子拼在一起可以坐 几人? (2)咖啡馆里有 60 张这样的正方形桌子,按下图方式每 4 张拼成一个大桌子,则 60 张桌子可 以拼成 15 张大桌子,共可坐多少人? (3)在(2)中若每 4 张桌子拼成一个大的正方形,共可坐多少人? (4)对于咖啡馆,哪种拼桌子的方式可以坐的人更多?

期中检测 一、选择题 1.A2.D3.A4.C5.B6.C7.B8.B 9.A10.A 二、填空题 11.答案不唯一,如把一枚硬币立在桌面上用力一转,形成一个球 12.213.-614.±615.> 16.2341 三、解答题 17解(a)原式-(+分引-24--24+日-242-240-184+9-23. (②)原式=4+6(-27)×()=-4+6-18=16 (3)原式=3a2.12a+9-25a2+5a-10=-222.7a-1. 18.解由a是绝对值等于2的负数,得a=-2; 由b是最小的正整数,得b=1; 由c的倒数的相反数是2,得c号 4ab3-[2abc+(5a2b3-7abc)-a2b3=4ab-(2abc+5a2b3-7abc-ab)=4a2b3-2abc- 5ab+7abc+ab=5abc. 当a=-2,b=1,c时,原式=5abc=5x-2)x1×分-5. 19.解(1)拼成的长方形的宽为m-n,长为m+n, 故拼成的长方形的周长为2(m-n+m+n)=4m. (2)当m=7,n=4时,拼成的长方形的面积为(m+n)(m-n)=(7+4)×(7-4)=11×3=33. 20.解(1)从左面看到的形状图有5种情形: ① ② ③ ④ ⑤ (2)由从正面看到的图形可知:从上面看到的图形中左边第一列只有1个小立方块:第二列每 个位置处最多有2个小立方块,且至少有一处有2个:第三列每个位置处最多有3个小立方 块,且至少有一处有3个.因此,n的最大值为1+2+2+3+3=11,最小值为1+1+2+1+3=8,从而n 的所有可能值为8,9,10,11. 21.解(1)(a+2.4)万人. (2)a+1.6+0.8+0.4=(a+2.8)万人,即10月3日游客人数最多 (3)(a+1.6)+(a+2.4)+(a+2.8)+(a+2.4)+(a+1.6)+(a+1.8)+(a+0.6)=7a+13.2,当a=2 时.7×2+13.2=27.2(万人).27.2×50=1360(万元). 22.解(1)两张桌子拼在一起可坐2+2+2=6(人),三张桌子拼在一起可坐2+2+2+2=8(人): n张桌子拼在一起可坐2(n+1)=(2n+2)人. (2)按题图方式每4张桌子拼成一个大桌子,那么一张大桌子可坐2×4+2=10(人)】 所以15张大桌子可坐10×15=150(人). (3)在(2)中,若每4张桌子拼成一个大的正方形桌子,则一张大正方形桌子可坐8人,15张大正 方形桌子可坐8×15=120(人). (4)由(2)(3)比较可知,该咖啡馆采用第一种拼摆方式可以坐的人更多」
期中检测 一、选择题 1.A 2.D 3.A 4.C 5.B 6.C 7.B 8.B 9.A 10.A 二、填空题 11.答案不唯一,如把一枚硬币立在桌面上用力一转,形成一个球 12.2 13.-6 14.±6 15.> 16.2 3 4 1 三、解答题 17.解 (1)原式=(- 3 4 + 1 6 - 3 8 )×(-24)=- 3 4 ×(-24)+ 1 6 ×(-24)- 3 8 ×(-24)=18-4+9=23. (2)原式=-4+6-(-27)×(- 2 3 )=-4+6-18=-16. (3)原式=3a 2 -12a+9-25a 2+5a-10=-22a 2 -7a-1. 18.解 由 a 是绝对值等于 2 的负数,得 a=-2; 由 b 是最小的正整数,得 b=1; 由 c 的倒数的相反数是-2,得 c= 1 2 , 所以 4a 2b 3 -[2abc+(5a 2b 3 -7abc)-a 2b 3 ]=4a 2b 3 -(2abc+5a 2b 3 -7abc-a 2b 3 )=4a 2b 3 -2abc- 5a 2b 3+7abc+a2b 3=5abc. 当 a=-2,b=1,c= 1 2时,原式=5abc=5×(-2)×1× 1 2 =-5. 19.解 (1)拼成的长方形的宽为 m-n,长为 m+n, 故拼成的长方形的周长为 2(m-n+m+n)=4m. (2)当 m=7,n=4 时,拼成的长方形的面积为(m+n)(m-n)=(7+4)×(7-4)=11×3=33. 20.解 (1)从左面看到的形状图有 5 种情形: (2)由从正面看到的图形可知:从上面看到的图形中左边第一列只有 1 个小立方块;第二列每 个位置处最多有 2 个小立方块,且至少有一处有 2 个;第三列每个位置处最多有 3 个小立方 块,且至少有一处有 3 个.因此,n 的最大值为 1+2+2+3+3=11,最小值为 1+1+2+1+3=8,从而 n 的所有可能值为 8,9,10,11. 21.解 (1)(a+2.4)万人. (2)a+1.6+0.8+0.4=(a+2.8)万人,即 10 月 3 日游客人数最多. (3)(a+1.6)+(a+2.4)+(a+2.8)+(a+2.4)+(a+1.6)+(a+1.8)+(a+0.6)=7a+13.2,当 a=2 时,7×2+13.2=27.2(万人).27.2×50=1 360(万元). 22.解 (1)两张桌子拼在一起可坐 2+2+2=6(人);三张桌子拼在一起可坐 2+2+2+2=8(人); n 张桌子拼在一起可坐 2(n+1)=(2n+2)人. (2)按题图方式每 4 张桌子拼成一个大桌子,那么一张大桌子可坐 2×4+2=10(人). 所以 15 张大桌子可坐 10×15=150(人). (3)在(2)中,若每 4 张桌子拼成一个大的正方形桌子,则一张大正方形桌子可坐 8 人,15 张大正 方形桌子可坐 8×15=120(人). (4)由(2)(3)比较可知,该咖啡馆采用第一种拼摆方式可以坐的人更多