
4.1几何图形 第1课时 立体图形与平面图形(一) 素能·达标U③ 0基础巩固 1.下列立体图形中,属于棱柱的是(B) A.圆柱 B.长方体 C球 D.圆锥 2.下列几何图形中与其他三个不是同一类的是(D) 3.下列说法:①教科书是长方形:②教科书是长方体,也是棱柱:③教科书的正面是 长方形.其中正确的是(C), A.①② B.①③ C.②③ D.①②③ 4.若一个棱柱有12个顶点,则下列说法中正确的是(C) A.这个棱柱有5条侧棱 B.这个棱柱有5个侧面 C.这个棱柱的底面是六边形 D这个棱柱是一个十二棱柱 5.如图,金字塔(图甲)和铅锤(图乙)所呈现的分别是棱锥和圆锥的形状 图甲 图乙
4.1 几何图形 第 1 课时 立体图形与平面图形(一) 1.下列立体图形中,属于棱柱的是(B). A.圆柱 B.长方体 C.球 D.圆锥 2.下列几何图形中与其他三个不是同一类的是(D). 3.下列说法:①教科书是长方形;②教科书是长方体,也是棱柱;③教科书的正面是 长方形.其中正确的是(C). A.①② B.①③ C.②③ D.①②③ 4.若一个棱柱有 12 个顶点,则下列说法中正确的是(C). A.这个棱柱有 5 条侧棱 B.这个棱柱有 5 个侧面 C.这个棱柱的底面是六边形 D.这个棱柱是一个十二棱柱 5.如图,金字塔(图甲)和铅锤(图乙)所呈现的分别是 棱锥 和 圆锥 的形状. 图甲 图乙

6请你举例说明生活中有哪些物体类似于圆柱:答案不唯一如:茶叶桶、水杯 等_,(写出两个即可) 1. 如图,把一个棱长为3的正方体的每个面等分成9个小正方形,然后沿每个面正中 心的一个正方形向里挖空(相当于挖去7个小正方体),所得到的几何体的表面积 是72 。能力提升 8.分别简述下列两组图形中两个图形的区别和联系. 图甲 图乙 答:图甲:圆柱和圆台的底面都是圆,侧面都是曲面,圆柱的两底面圆相同,而圆台的 两底面圆不同 图乙:三棱柱和三棱台的底面都是三角形,但是三棱柱两底面三角形相同,三棱台 的两底面三角形不同:都有三个侧面,但是三棱柱的侧面是长方形,三棱台的侧面 是梯形 9.观察下列棱柱,思考并回答问题: P (1)每个棱柱的上底面与下底面相同吗? (2)每个棱柱的侧面是什么图形? (3)侮个棱柱的侧棱的长度之间有什么关系? (4)侧面的个数与底面多边形的边数有什么关系? 答案:(1)相同 (2)第一个棱柱的侧面为正方形,其余的棱柱的侧面都为长方形
6.请你举例说明生活中有哪些物体类似于圆柱: 答案不唯一,如:茶叶桶、水杯 等 .(写出两个即可) 7. 如图,把一个棱长为 3 的正方体的每个面等分成 9 个小正方形,然后沿每个面正中 心的一个正方形向里挖空(相当于挖去 7 个小正方体),所得到的几何体的表面积 是 72 . 8.分别简述下列两组图形中两个图形的区别和联系. 图甲 图乙 答:图甲:圆柱和圆台的底面都是圆,侧面都是曲面,圆柱的两底面圆相同,而圆台的 两底面圆不同. 图乙:三棱柱和三棱台的底面都是三角形,但是三棱柱两底面三角形相同,三棱台 的两底面三角形不同;都有三个侧面,但是三棱柱的侧面是长方形,三棱台的侧面 是梯形. 9.观察下列棱柱,思考并回答问题: (1)每个棱柱的上底面与下底面相同吗? (2)每个棱柱的侧面是什么图形? (3)每个棱柱的侧棱的长度之间有什么关系? (4)侧面的个数与底面多边形的边数有什么关系? 答案:(1)相同 (2)第一个棱柱的侧面为正方形,其余的棱柱的侧面都为长方形
(3)相等 (4)相等 10.以给定的图形o0△△一(两个圆、两个三角形、两条平行直线)为组件 构思独特且有意义的图形 答案:答案不唯一,如: 第2课时立体图形与平面图形(二) 素能.达标③ 0基础巩固 1.下面4个几何体中,从正面看,得到的图形与其他几何体不同的是(C). 2.由几个相同的小正方体搭成的几何体从3个方向看到的图形如图所示,则搭成 这个几何体的小正方体的个数是(B), 从正面看 从左面看 从上面看 A.3 B.4 C.5 D.6 3.下列各项中,是三棱柱的侧面展开图的是(A)
(3)相等 (4)相等 10.以给定的图形“○○ △△ ”(两个圆、两个三角形、两条平行直线)为组件, 构思独特且有意义的图形. 答案:答案不唯一,如: 第 2 课时 立体图形与平面图形(二) 1.下面 4 个几何体中,从正面看,得到的图形与其他几何体不同的是(C). 2.由几个相同的小正方体搭成的几何体从 3 个方向看到的图形如图所示,则搭成 这个几何体的小正方体的个数是(B). A.3 B.4 C.5 D.6 3.下列各项中,是三棱柱的侧面展开图的是(A)

4.正方体的展开图如图所示,则原正方体相对两个面上的数字和最小为(C)】 A.4 B.6 C.7 D.8 5写出一个从正面、左面、上面看所得到的图形都相同的几何体:答案不唯一 如:正方体、球, 6.由若干个大小相同的小正方体堆砌而成的几何体如图所示,那么从左面_(填 “正面“左面”或“上面”)看得到的图形的面积最小 7.根据下列立体图形的展开图,填写立体图形的名称 口中分 答案:长方体三棱柱三棱锥 。能力提升 8.一个正方体的展开图如图所示,标注了字母A的是正方体的正面,如果正方体的 左面与右面标注的式子相等,请求出x的值
4.正方体的展开图如图所示,则原正方体相对两个面上的数字和最小为(C). A.4 B.6 C.7 D.8 5.写出一个从正面、左面、上面看所得到的图形都相同的几何体: 答案不唯一, 如:正方体、球 . 6.由若干个大小相同的小正方体堆砌而成的几何体如图所示,那么从 左面 (填 “正面”“左面”或“上面”)看得到的图形的面积最小. 7.根据下列立体图形的展开图,填写立体图形的名称. 答案:长方体 三棱柱 三棱锥 8.一个正方体的展开图如图所示,标注了字母 A 的是正方体的正面,如果正方体的 左面与右面标注的式子相等,请求出 x 的值
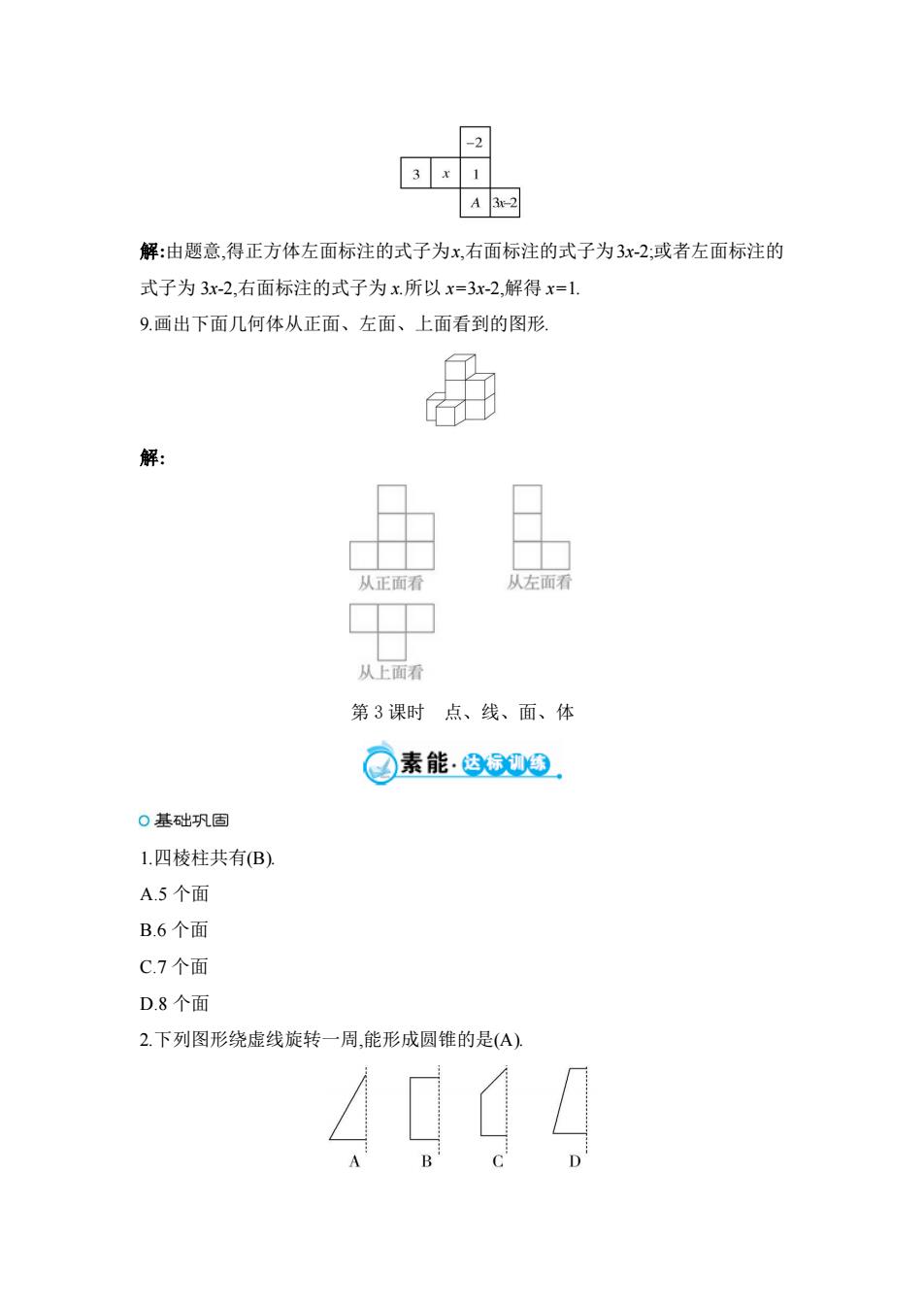
-2 3x 1 A3x-2 解:由题意,得正方体左面标注的式子为x,右面标注的式子为3x-2:或者左面标注的 式子为3x-2,右面标注的式子为x所以x=3x-2,解得x=1. 9.画出下面几何体从正面、左面、上面看到的图形 解: 从正面看 从左面看 从上面看 第3课时 点、线、面、体 ©素能:500. 0基础巩固 1.四棱柱共有B) A.5个面 B.6个面 C.7个面 D.8个面 2.下列图形绕虚线旋转一周,能形成圆锥的是(A), 40〔4
解:由题意,得正方体左面标注的式子为x,右面标注的式子为3x-2;或者左面标注的 式子为 3x-2,右面标注的式子为 x.所以 x=3x-2,解得 x=1. 9.画出下面几何体从正面、左面、上面看到的图形. 解: 第 3 课时 点、线、面、体 1.四棱柱共有(B). A.5 个面 B.6 个面 C.7 个面 D.8 个面 2.下列图形绕虚线旋转一周,能形成圆锥的是(A)
3.如图所示,一只蚂蚁从正方体的顶点A沿着棱爬向点B,只能经过3条棱,则其走 法有(C) A8种 B.7种 C.6种 D.5种 4.如图,在方格中有4个图案①②③④,其中面积相等的是(A) ① ② ③ ④ A.①和② B.②和③ C.②和④ D.①和④ 5.把一张白纸对折后,在纸上会出现一道痕迹,用数学知识解释为面与面相交形 成线 6.一个正方体的木块砍掉一个角后,剩余的图形会有7个面, 7.一个多面体的面数为6棱数为12,则其顶点的个数为8 。能力提升 8.如图,求直角三角形ABC绕直角边AB所在直线旋转一周所得的几何体的体积. 4 cm 3 cm 解:由题意知,所得几何体为圆锥,底面积为9πcm2,高为4cm, 所以体积为片×9m×4=12π(cm3)
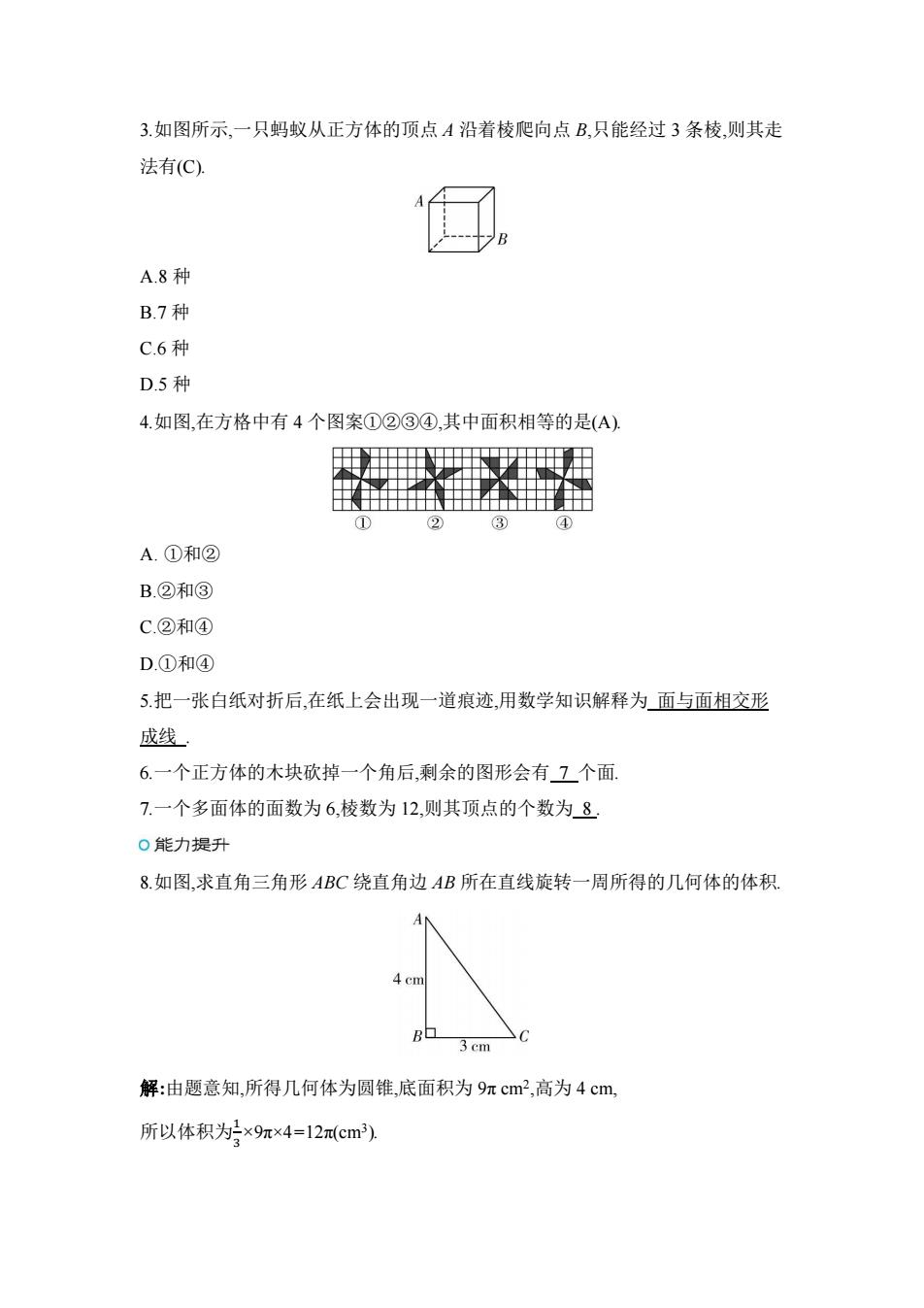
3.如图所示,一只蚂蚁从正方体的顶点 A 沿着棱爬向点 B,只能经过 3 条棱,则其走 法有(C). A.8 种 B.7 种 C.6 种 D.5 种 4.如图,在方格中有 4 个图案①②③④,其中面积相等的是(A). A. ①和② B.②和③ C.②和④ D.①和④ 5.把一张白纸对折后,在纸上会出现一道痕迹,用数学知识解释为 面与面相交形 成线 . 6.一个正方体的木块砍掉一个角后,剩余的图形会有 7 个面. 7.一个多面体的面数为 6,棱数为 12,则其顶点的个数为 8 . 8.如图,求直角三角形 ABC 绕直角边 AB 所在直线旋转一周所得的几何体的体积. 解:由题意知,所得几何体为圆锥,底面积为 9π cm2 ,高为 4 cm, 所以体积为1 3 ×9π×4=12π(cm3 )