
目录 第一章丰富的图形世界 1 生活中的立体图形… 第1课时立体图形的认识 第2课时图形的构成… 2展开与折叠…。 第1课时正方体的展开与折叠… 5 第2课时柱体、锥体的展开与折叠… 3截一个几何体 10 4从三个方向看物体的形状 12 第二章 有理数及其运算 1有理数 14 2数轴… 3绝对值… 18 4有理数的加法.… 21 第1课时有理数的加法法则… 2 第2课时有理数的加法运算律… 23 5有理数的减法… 25 6有理数的加减混合运算… 27 第1课时有理数的加减混合运算 27 第2课时有理数加减的简便运算… … 28 第3课时有理数加减运算的简单应用… 30 7有理数的乘法………… 33 第1课时有理数的乘法法则… 33 第2课时 有理数的乘法运算律· 35 8有理数的除法 37 9有理数的乘方 39 10科学记数法 2 11有理数的混合运算 44 12用计算器进行运算 46 第三章整式及其加减 1 字母表示数 公 2代数式 50 第1课时认识代数式… 50 第2课时求代数式的值… 52 3整式 … 55 4整式的加减 57 第1课时合并同类项… 57 第2课时去括号 59 1

目录 第3课时整式的加减 61 5探索与表达规律… 63 第四章基本平面图形 1线段、射线、直线 66 2比较线段的长短 68 3角… 71 4角的比较 74 5多边形和圆的初步认识 76 第五章一元一次方程 1认识一元一次方程…79 第1课时一元一次方程…79 第2课时等式的基本性质… 81 2求解一元一次方程… 83 第1深时解一元一次方程—移项… 83 第2课时解一元一次方程一去括号… 85 第3课时解一元一次方程一去分母… 87 3应用一元一次方程一水箱变高了 89 4应用一元一次方程一打折销售 91 5应用一元一次方程一“希望工程”义演 0… 93 6应用一元一次方程—追赶小明 95 第六章数据的收集与整理 1数据的收集 98 2普查和抽样调查… 101 3数据的表示… 103 第1课时扇形统计图… 103 第2课时频数直方图 106 4统计图的选择… 109 第1课时统计图的选择 109 第2课时正确识别统计图 111 检 测 第一章检测 ..115 第四章检测 129 第二章检测 … 119 第五章检测 132 第三章检测 … 122 第六章检测 … 136 期中检测 4 125 期末检测 … 140 2

第一章 丰富的图形世界 1 生活中的立体图形 第1课时 立体图形的认识 基础·自主梳理 1.几何体及其分类 相同,侧面的形状都是平行四边形.棱柱 常见的几何体有正方体、长方体、圆柱、圆 可以分为直棱柱和斜棱柱,直棱柱的各个侧 锥、球、核柱· 面都是长方形 几何体可以按柱体、锥体、球体进行分 (2)n棱柱有2n个顶点,3n条棱,n 类,也可以按组成面的平或曲进行分类 条侧棱,(十2)个面,2个底面,n个侧面. 温馨提示 3.棱柱与圆柱的异同 几何体的分类没有固定的标准,但分类 相同点:它们的两个底面都分别是形状、 的前提是要确定统一的标准,做到不重不漏. 大小相同,且相互平行的图形: 不同点:棱柱的侧面由平面图形组成, 2.棱柱的有关概念与特征 而圆柱的侧面是曲面;棱柱的底面是多边 (1)在棱柱中,相邻两个面的交线叫做 形,而圆柱的底面是圆 核,相邻两个侧面的交线叫做侧核.棱柱的所 有侧棱长都相等·棱柱的上、下底面的形状 核心·重难探究 知识点一常见的儿何体与分类 状、大小一样,且互相平行 【例1】如图,下列几何体中,(1)柱体有 听课笔记: ①③④;(2)圆锥有②;(3)球有⑤.(填 序号)》 2 3 思路点拨柱体有两个底面,它们的形

家庭作业·数学·七年级·上册·配北师大版 【方法归纳】 观地数一数获得结论. 圆柱 解(1)这个六棱柱一共有8个面,其中有2 常 柱体 直棱柱(如长方体、正方体等)》 个底面和6个侧面;底面都是六边形,侧面都 的 棱柱 几 斜棱柱 是长方形;2个底面的形状、面积完全相同,6 何 锥体 个侧面的形状、面积也完全相同. 球 (2)这个六棱柱一共有18条棱,侧核的长 度都是4cm,其他核的长度都是5cm. 知识点二 棱柱的有关概念与特征 【例2】一个六棱柱模型如图 【方法归纳】 所示,它的底面边长都是5cm,侧 棱长是4cm. 棱柱的所有侧 底面 顶点 (1)这个六棱柱一共有多少个面?它们 棱长都相等: 棱柱 棱柱的上、下底 分别是什么形状?哪些面的形状、面积完全 侧 侧棱 的特征 面的形状相同; 相同? 侧面的形状都 (2)这个六棱柱一共有多少条棱?它们 是平行四边形 的长度分别是多少? 棱柱的底面图形有几条边,这个棱柱就是 思路点拨可根据棱柱的面数、顶点数、 棱柱 几棱柱;棱柱按侧棱与底面是否垂直,可 棱的条数的规律公式作答,也可根据图形直 的分类 分为直棱柱和斜棱柱 新知· 训练巩固 1.按组成面的平或曲划分,下面与圆柱为同 A.四棱柱是正方体 一类的几何体是(D). B.棱柱的侧棱长不一定相等 A.棱柱 B.长方体 C.五棱柱有7个面 C.正方体 D.圆锥 D.正方体是四棱柱,长方体不是四棱柱 2.下列说法正确的是(C). 3.棱柱的侧面是平行四边形 素能·演练提升 1.下列图形不是立体图形的是(D). A.球 B.圆柱 C.圆锥 D.圆 B 2.(2021·贵州贵阳中考)下列几何体中,圆 3.两个完全相同的正方体,将一面完全重合, 柱体是(C). 构成的几何体的面数为(D). A.12 B.11 C.10 D.6 2
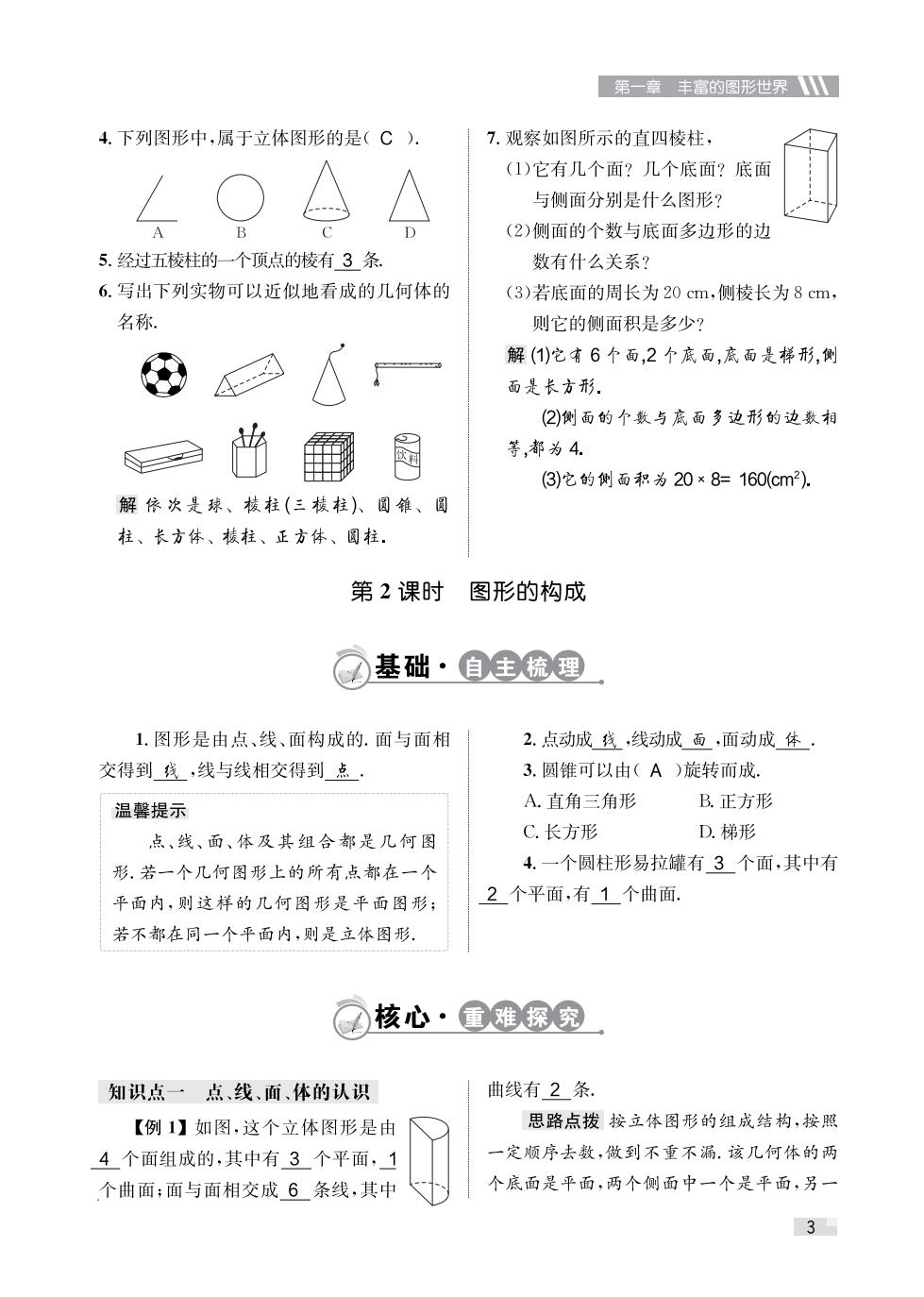
第一章丰富的图形世界 4.下列图形中,属于立体图形的是(C). 7.观察如图所示的直四棱柱, (1)它有几个面?几个底面?底面 △△ 与侧面分别是什么图形? (2)侧面的个数与底面多边形的边 5.经过五棱柱的一个顶点的棱有3条, 数有什么关系? 6.写出下列实物可以近似地看成的几何体的 (3)若底面的周长为20cm,侧棱长为8cm, 名称 则它的侧面积是多少? 解(1)它有6个面,2个底面,底面是梯形,侧 面是长方形. (2)侧面的个数与底面多边形的边数相 等,都为4. (3)它的侧面积为20×8=160(cm2). 解依次是球、核柱(三棱柱)、圆锥、圆 柱、长方体、核柱、正方体、圆柱 第2课时 图形的构成 基础·自主梳理 1.图形是由点、线、面构成的.面与面相 2.点动成线,线动成面,面动成体· 交得到线,线与线相交得到点 3.圆锥可以由(A)旋转而成. 温馨提示 A.直角三角形 B.正方形 点、线、面、体及其组合都是几何图 C.长方形 D.梯形 形.若一个几何图形上的所有点都在一个 4.一个圆柱形易拉罐有3个面,其中有 平面内,则这样的几何图形是平面图形; 2个平面,有1个曲面, 若不都在同一个平面内,则是立体图形. 核心·重难探究 知识点一点、线、面、体的认识 曲线有2条. 【例1】如图,这个立体图形是由 思路点拨按立体图形的组成结构,按照 4个面组成的,其中有3个平面,1 一定顺序去数,做到不重不漏.该几何体的两 个曲面;面与面相交成6条线,其中 个底面是平面,两个侧面中一个是平面,另一 3

儿家庭作业·数学·七年级·上册·配北师大版 个是曲面:两个底面与曲侧面相交成两条曲 线,两个底面与平侧面相交成两条直线,两个 ΛA4 侧面相交成两条直线. B 听课笔记: 思路点拨直角三角形沿较长直角边所 在直线旋转一周形成怎样的几何体?沿较短 直角边呢?沿斜边呢? 听课笔记: 【方法归纳】 线与面的数法:对于几何体,面与面相交 得到线,线与线相交得到点.数面时,可先数 底面,再数侧面:数线时,可先数底面与侧面 【方法归纳】 相交所成的线,再数侧面与侧面相交所成 1.平面图形绕轴旋转时,关键要看两点: 的线。 (1)看主要的线的转动情况; 知识点二点、线、面、体的关系 (2)看图形的运动轨迹, 【例2】如图,将直角三角形ABC绕一条 2.点、线、面、体之间的关系如图所示: 动 边所在的直线旋转一周后形成的几何体不可 直线 平面 能是(C. 点、 动 动 动体 曲线动、 曲面 新知·训练巩固 1.下面的几何体中,既含有平面又含有曲面 3.下列现象说明了什么道理? 的是(C). (1)我们把笔尖看作一个点,当笔尖在纸上 A.正方体B.长方体C.圆锥体D.球体 移动时,就能画出线; 2.古埃及的金字塔是一种类似于方锥体的建 (2)时钟秒针旋转时,形成一个圆面: 筑,请你数一数,它是由5个面围成的,面 (3)一张长方形硬纸板绕它的一条边旋转 与面相交成8条线,有5个顶点. 周,形成了一个圆柱 解(1)点动成线. (2)线动成面. (3)面动成体. 4

第一章丰富的图形世界 素能·演练提升 1.将左图所示的直角梯形绕直线1旋转一周, 4.正方体有8个顶点,12条棱,6个面, 得到的立体图形是(C). 这些面都是平面. 5.流星划破夜空,留下美丽的弧线,这说明了 bge日 点动成线;一条拉直的细线切开了一块豆 B 腐,这说明了线动成面;把一枚硬币立在 2.一个长和宽分别为4cm和 桌面上用力一转,形成一个球,这说明了 3cm的长方形如图所示,将 面动成体, 其按一定方式进行旋转,能 6.如图,圆锥是由几个面围成的?它们是平 得到不同圆柱的个数为(D). 的面还是曲的面?它们的交线是直的还是 A.1 B.2 C.4 D.无数 曲的?棱柱呢?过棱柱的一个顶点有几条边? 3.将下列三角形绕虚线1旋转一周,可以得到 如左下图所示的几何体的是(C). 解圆锥是由两个面围成的,侧面是曲面,底 面是平面,它们的交线是曲线;题图中的棱 柱由5个面围成,都是平面,它们的交线都 是直线,过核柱的一个项点有3条边. 2 展开与折叠 第1课时 正方体的展开与折叠 基础·自主梳理 1.要得到一个正方体的展开图,至少需 (1,4,1)型 要剪开7条棱:要得到n棱柱的展开图,需 四即吧吧即中 要剪开(2一1)条棱, 2,3.1)型 (2,2,2)型(3.3)型 2.一个正方体的展开图共有11种 西中即中 5

家庭作业·数学·七年级·上册·配北师大版 核心·重难探究 知识点正方体的展开与折叠 【例题】水平放置的正方体 祝 的六个面分别用“前面、后面、下 你 前程 面、上面、左面、右面”表示.一个 似 【方法归纳】 正方体的平面展开图如图所示, 锦 当正方体的表面展开图中有三个正方形 若图中“锦”为前面,“似”为下面,“前”为后 在同一行或一列时,中间隔一个正方形的两 面,则“祝”为正方体的上面. 个正方形折叠后相对:当没有三个正方形在 思路点拨展开图折叠成正方体后,“祝” 一行或一列时,可沿同一个方向移动其中一 字的对面是“似”字,则“祝”为正方体的上面 个小正方形成一行或一列即可,即若两个正 听课笔记: 方形之间隔着一行或一列,则折叠后也是相 对的. 新知·训练巩固 1.(2021·贵州黔西南中考》 4.如图,是由6个相同的正方形拼成的图形, 如图是一个正方体的展开 习雷锋 精 请你将其中一个正方形移动到合适的位 图,把它折叠成正方体后, 神 置,使它与另5个正方形能拼成一个正方 有“学”字一面的相对面上的字是(D). 体的表面展开图.(请在图中将要移动的那 A.雷 B.锋 C.精 D.神 个正方形涂黑,并画出移动后的正方形) 2.下列哪个图形是正方体的展开图(B), 解如图所示(答紫不唯一)】 3.下列平面展开图都是由5个大小相同的正 方形组成的,其中沿正方形的边不能折成 无盖小方盒的是(B)
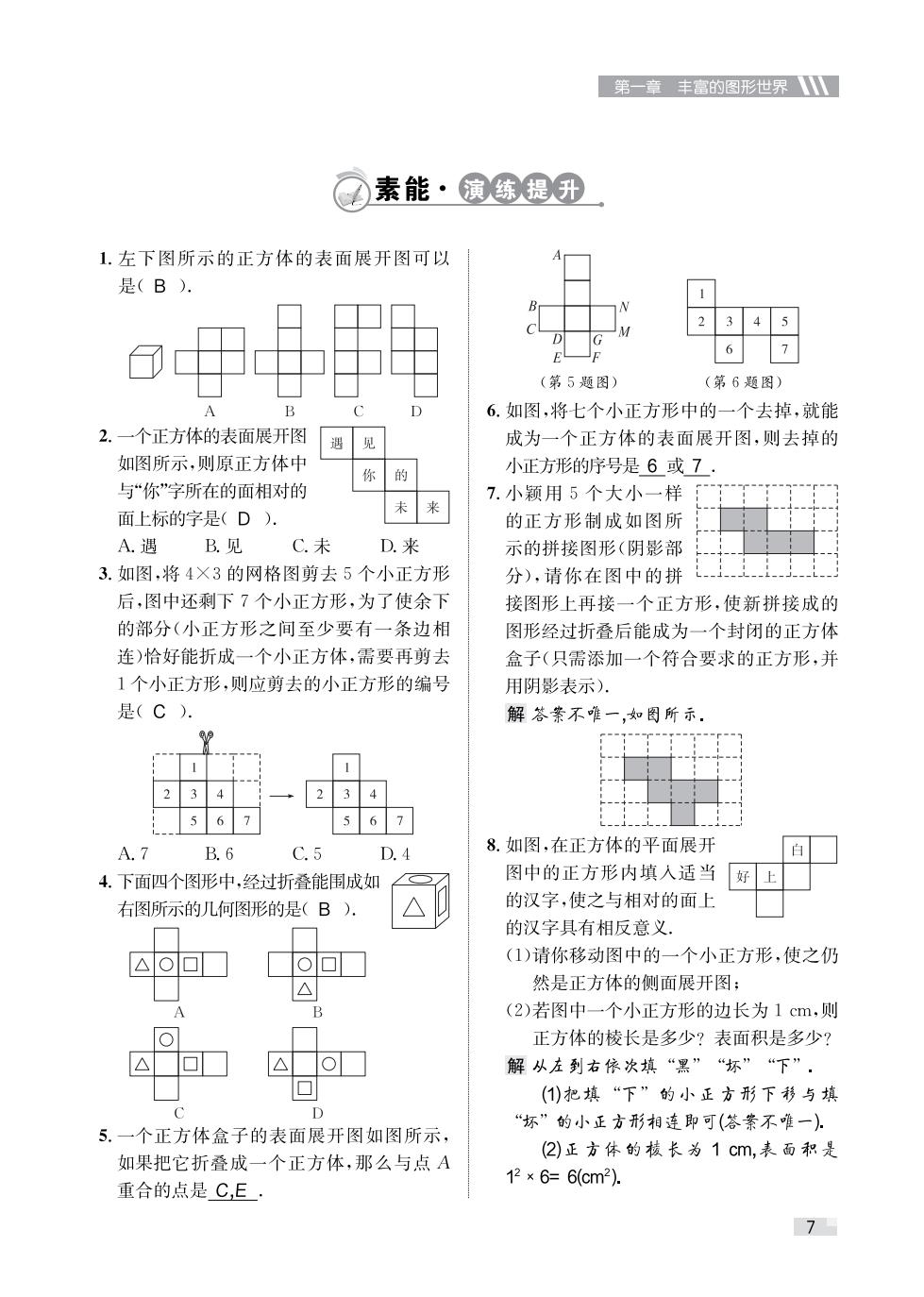
第一章 丰富的图形世界 素能·演练提升 1.左下图所示的正方体的表面展开图可以 是(B). E (第5题图) (第6题图) D 6.如图,将七个小正方形中的一个去掉,就能 2.一个正方体的表面展开图 见 成为一个正方体的表面展开图,则去掉的 如图所示,则原正方体中 你 的 小正方形的序号是6或7 与“你”字所在的面相对的 7.小颖用5个大小一样 未 来 面上标的字是(D). 的正方形制成如图所 A.遇 B.见 C.未 D.来 示的拼接图形(阴影部 3.如图,将4×3的网格图剪去5个小正方形 分),请你在图中的拼 后,图中还剩下7个小正方形,为了使余下 接图形上再接一个正方形,使新拼接成的 的部分(小正方形之间至少要有一条边相 图形经过折叠后能成为一个封闭的正方体 连)恰好能折成一个小正方体,需要再剪去 盒子(只需添加一个符合要求的正方形,并 1个小正方形,则应剪去的小正方形的编号 用阴影表示), 是(C). 解答案不唯一,如图所示, A.7 B.6 C.5 D.4 8.如图,在正方体的平面展开 白 4.下面四个图形中,经过折叠能围成如 图中的正方形内填入适当 好 右图所示的几何图形的是(B). 的汉字,使之与相对的面上 的汉字具有相反意义, △O▣ (1)请你移动图中的一个小正方形,使之仍 △ 然是正方体的侧面展开图: (2)若图中一个小正方形的边长为1cm,则 正方体的棱长是多少?表面积是多少? 解从左到右依次填“黑”“杯”“下”. (1)把填“下”的小正方形下移与填 D “杯”的小正方形相连即可(答紫不唯一) 5.一个正方体盒子的表面展开图如图所示, (2)正方体的核长为1cm,表面积是 如果把它折叠成一个正方体,那么与点A 12×6=6(cm2). 重合的点是C,E· 7
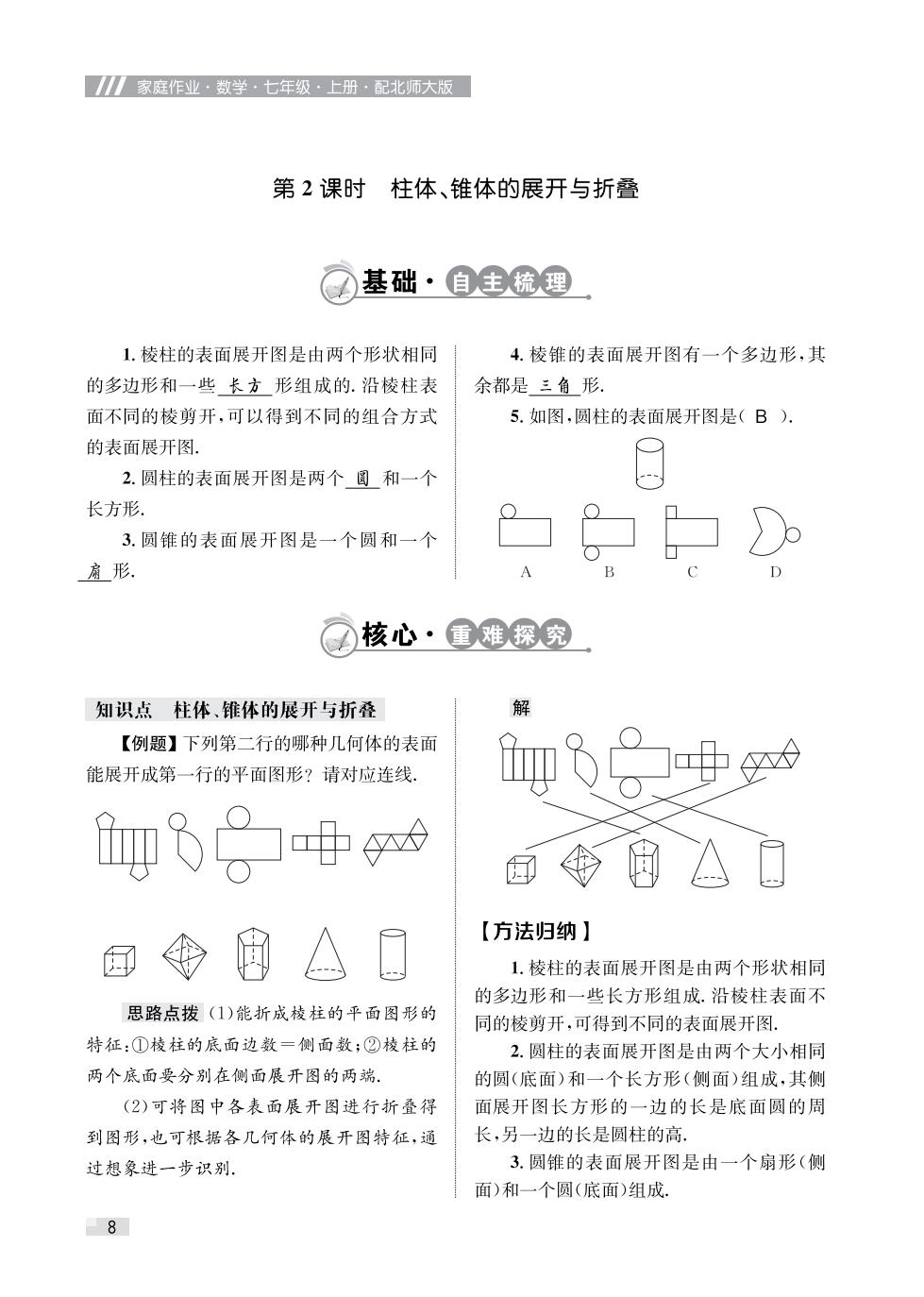
1家庭作业·数学·七年级·上册·配北师大版 第2课时柱体、锥体的展开与折叠 基础·自主梳理 1.棱柱的表面展开图是由两个形状相同 4.棱锥的表面展开图有一个多边形,其 的多边形和一些长方形组成的.沿棱柱表 余都是三角形 面不同的棱剪开,可以得到不同的组合方式 5.如图,圆柱的表面展开图是(B). 的表面展开图. 2.圆柱的表面展开图是两个圆和一个 长方形 3.圆锥的表面展开图是一个圆和一个 扇形 Q核心·重难探究 知识点柱体、锥体的展开与折叠 解 【例题】下列第二行的哪种几何体的表面 能展开成第一行的平面图形?请对应连线, ig8G时d 即6。中 【方法归纳】 1.棱柱的表面展开图是由两个形状相同 的多边形和一些长方形组成.沿棱柱表面不 思路点拨(1)能折成棱柱的平面图形的 同的棱剪开,可得到不同的表面展开图. 特征:①棱柱的底面边数=侧面数;②棱柱的 2.圆柱的表面展开图是由两个大小相同 两个底面要分别在侧面展开图的两端 的圆(底面)和一个长方形(侧面)组成,其侧 (2)可将图中各表面展开图进行折叠得 面展开图长方形的一边的长是底面圆的周 到图形,也可根据各几何体的展开图特征,通 长,另一边的长是圆柱的高 过想象进一步识别. 3.圆锥的表面展开图是由一个扇形(侧 面)和一个圆(底面)组成 8