
家庭侯亚 3.简单的轴对称图形 第3课时 角平分线
3.简单的轴对称图形 第3课时 角平分线

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.角是轴对称 图形,角平分线所在的直线是它的对称 轴. 2.角平分线上的点到这个角的两边 的距离相等 温馨提示 角平分线的性质主要用来说明两条线段相等,注意距离相等 是用两条垂线段相等来表示的、 3.已知在△ABC中,∠C=90°,BD平分∠ABC交AC于点D.若 DC=2.5,则点D到AB的距离为 2.5 导航页
导航页 基础自主梳理 1.角是 图形, 所在的直线是它的对称 轴. 2.角平分线上的点到这个角的 的距离相等. 温馨提示 角平分线的性质主要用来说明两条线段相等,注意距离相等 是用两条垂线段相等来表示的. 3.已知在△ABC中,∠C=90° ,BD平分∠ABC交AC于点D.若 DC=2.5,则点D到AB的距离为 . 轴对称 角平分线 两边 2.5
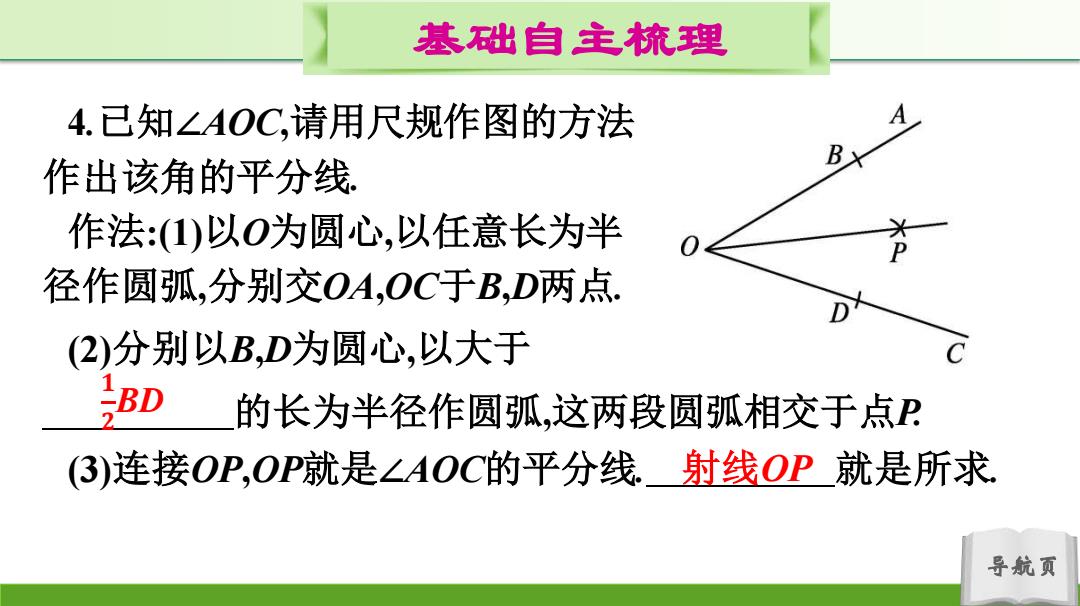
基础自主梳理 4.已知∠AOC,请用尺规作图的方法 作出该角的平分线 作法:(1)以O为圆心,以任意长为半 径作圆弧,分别交OA,OC于B,D两点. (2)分别以B,D为圆心,以大于 BD 的长为半径作圆弧,这两段圆弧相交于点P (3)连接OP,OP就是∠AOC的平分线射线OP就是所求 导航页
导航页 基础自主梳理 4.已知∠AOC,请用尺规作图的方法 作出该角的平分线. 作法:(1)以O为圆心,以任意长为半 径作圆弧,分别交OA,OC于B,D两点. (2)分别以B,D为圆心,以大于 的长为半径作圆弧,这两段圆弧相交于点P. (3)连接OP,OP就是∠AOC的平分线. 就是所求. 𝟏 𝟐 BD 射线OP

核心重难探究 知识点一角平分线的性质 【例1】如图,BD是∠ABC的平分线,DE⊥AB, DF⊥BC,垂足分别为E,F若△ABC的面积为 E 36cm2,AB=18cm,BC=12cm,求DE的长 思路点拨:(1)DE与图形中的哪一条线段的长度 相等?你的依据是什么?(2)△ABC的面积可以看 成哪两个三角形的面积和?这两个三角形有什么相同点? 导航页
导航页 核心重难探究 知识点一 角平分线的性质 【例1】如图,BD是∠ABC的平分线,DE⊥AB, DF⊥BC,垂足分别为E,F.若△ABC的面积为 36 cm2 ,AB=18 cm,BC=12 cm,求DE的长. 思路点拨:(1)DE与图形中的哪一条线段的长度 相等?你的依据是什么?(2)△ABC的面积可以看 成哪两个三角形的面积和?这两个三角形有什么相同点?

核心心重难探究 解:令△ABC,△ABD,△BCD的面积分别为S△4BC,S△4BD, S△BCD .BD是∠ABC的平分线,DE⊥AB,DF⊥BC,'DE=DF .SAABC=36 cm2,4B=18 cm,BC=12 cm, '.SMBD+SABCD-AB-DE+BC-DF-36, 即218DE+×12DE=36, 解得DE号 cm. 导航页
导航页 核心重难探究 解:令△ABC,△ABD,△BCD的面积分别为S△ABC,S△ABD, S△BCD, ∵BD是∠ABC的平分线,DE⊥AB,DF⊥BC,∴DE=DF. ∵S△ABC =36 cm2 ,AB=18 cm,BC=12 cm, ∴S△ABD+S△BCD= 𝟏 𝟐 AB·DE+𝟏 𝟐 BC·DF=36, 即 𝟏 𝟐 ×18DE+𝟏 𝟐 ×12DE=36, 解得 DE=𝟏𝟐 𝟓 cm

核心重难探究 【方法归纳】 熟知角平分线上的点到角两边的距离相等是解答此题的关 键, 导航页
导航页 核心重难探究 【方法归纳】 熟知角平分线上的点到角两边的距离相等是解答此题的关 键

核心重难探究 知识点二角平分线的画法 【例2】如图,已知△ABC,∠B=90°,按下列 要求作图(尺规作图,不写作图步骤,保留作图痕迹) (1)作∠C的平分线与AB相交于点D,在AC边上 取一点E,使CE=CB,连接DE; B (2)根据所作的图形写出一对相等的线段和一对相等的锐角 不包括CE=CB,∠ECD=∠BCD),并说明理由. 导航页
导航页 核心重难探究 知识点二 角平分线的画法 【例2】如图,已知△ABC,∠B=90° ,按下列 要求作图.(尺规作图,不写作图步骤,保留作图痕迹) (1)作∠C的平分线与AB相交于点D,在AC边上 取一点E,使CE=CB,连接DE; (2)根据所作的图形写出一对相等的线段和一对相等的锐角 (不包括CE=CB,∠ECD=∠BCD),并说明理由

核心重难探究 思路点拨:(1)根据作角平分线的作法作图可得点D;再以C为 圆心,CB长为半径画孤,交AC于点E,最后连接DE即可; 2)首先证明△CBD烂△CED,然后根据全等三角形的性质可 得DB=DE,∠EDC=∠BDC 导航页
导航页 核心重难探究 思路点拨:(1)根据作角平分线的作法作图可得点D;再以C为 圆心,CB长为半径画弧,交AC于点E,最后连接DE即可; (2)首先证明△CBD≌△CED,然后根据全等三角形的性质可 得DB=DE,∠EDC=∠BDC
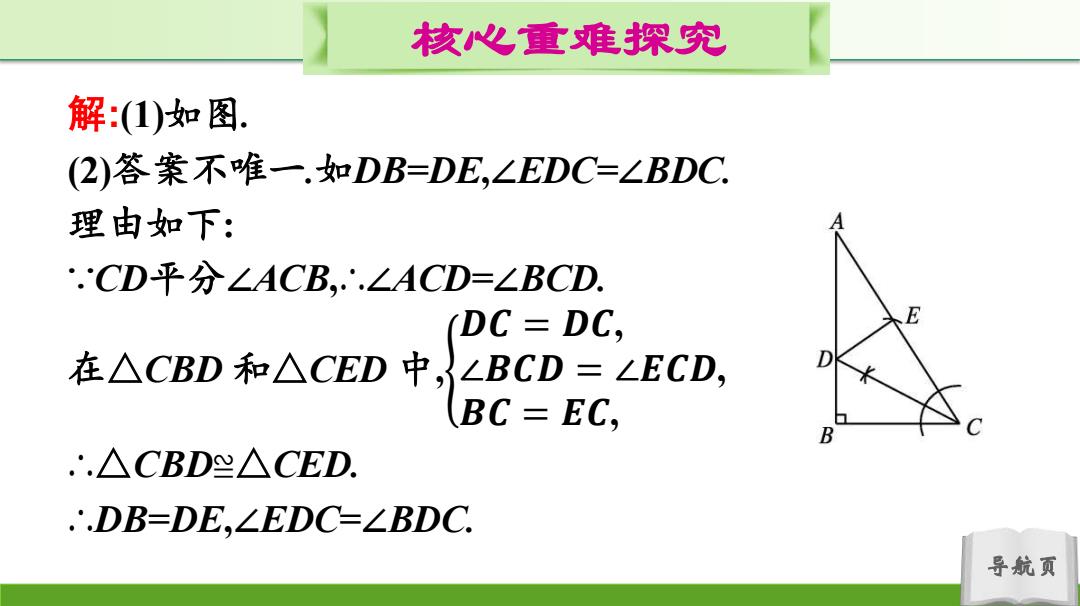
核心重难探究 解:1)如图. (2)答案不唯一.如DB=DE,∠EDC=∠BDC. 理由如下: .CD平分∠ACB,.∴.∠ACD=∠BCD. (DC=DC, 在△CBD和△CED中,}LBCD=∠ECD, D (BC=EC, .'.△CBD'△CED ∴.DB=DE,∠EDC=∠BDC. 导航页
导航页 核心重难探究 解:(1)如图. (2)答案不唯一.如DB=DE,∠EDC=∠BDC. 理由如下: ∵CD平分∠ACB,∴∠ACD=∠BCD. 在△CBD 和△CED 中, 𝑫𝑪 = 𝑫𝑪, ∠𝑩𝑪𝑫 = ∠𝑬𝑪𝑫, 𝑩𝑪 = 𝑬𝑪, ∴△CBD≌△CED. ∴DB=DE,∠EDC=∠BDC