
家庭们亚 3.平行线的性质 第1课时 平行线的性质
3.平行线的性质 第1课时 平行线的性质

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1两条平行直线被第三条直线所截,同位角相等 简称 为:两直线平行,同位角相等 2.两条平行直线被第三条直线所截,内错角相等简称 为:两直线平行,内错角相等 3.两条平行直线被第三条直线所截,同旁内角互补简 称为:两直线平行,同旁内角互补 导航页
导航页 基础自主梳理 1.两条平行直线被第三条直线所截,同位角 .简称 为:两直线平行,同位角 . 2.两条平行直线被第三条直线所截,内错角 .简称 为:两直线平行,内错角 . 3.两条平行直线被第三条直线所截,同旁内角 .简 称为:两直线平行,同旁内角 . 相等 相等 相等 相等 互补 互补

基础自主梳理 温馨提示 1.“同位角相等、内错角相等、同旁内角互补”是平行线的 特有性质,在使用时,切不可忽略前提条件“两直线平行”. 2.当两直线不平行时,同位角、内错角就不相等,同旁内角也 不互补 导航页
导航页 基础自主梳理 温馨提示 1. “同位角相等、内错角相等、同旁内角互补”是平行线的 特有性质,在使用时,切不可忽略前提条件“两直线平行” . 2.当两直线不平行时,同位角、内错角就不相等,同旁内角也 不互补
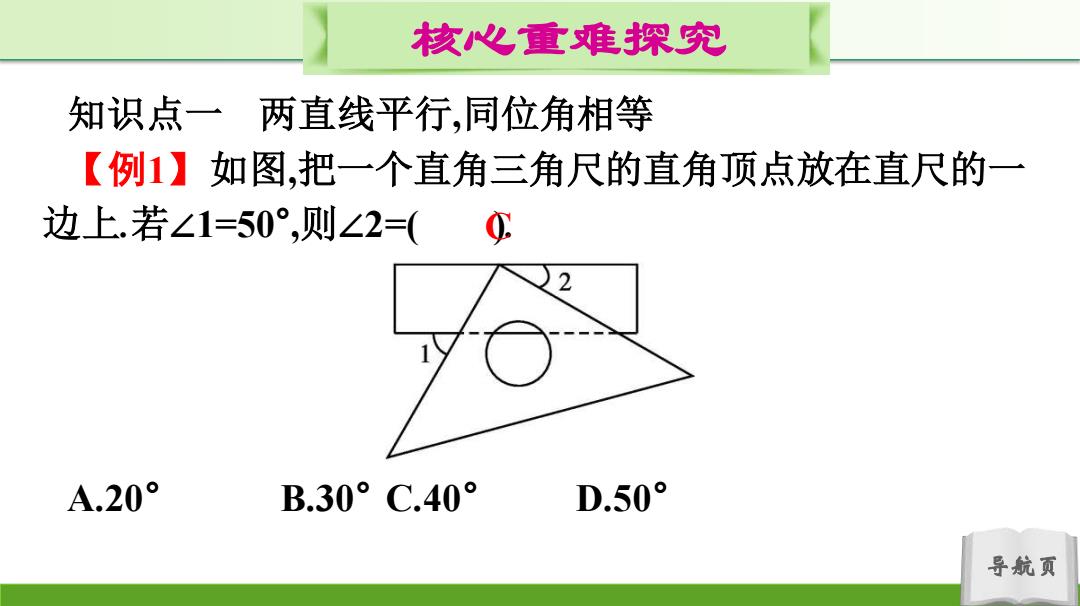
核心重难探究 知识点一 两直线平行,同位角相等 【例1】如图,把一个直角三角尺的直角顶点放在直尺的一 边上若∠1=50°,则∠2=(0 A.20° B.30°C.40° D.50° 导航页
导航页 核心重难探究 知识点一 两直线平行,同位角相等 【例1】如图,把一个直角三角尺的直角顶点放在直尺的一 边上.若∠1=50° ,则∠2=( ). A.20° B.30° C.40° D.50° C
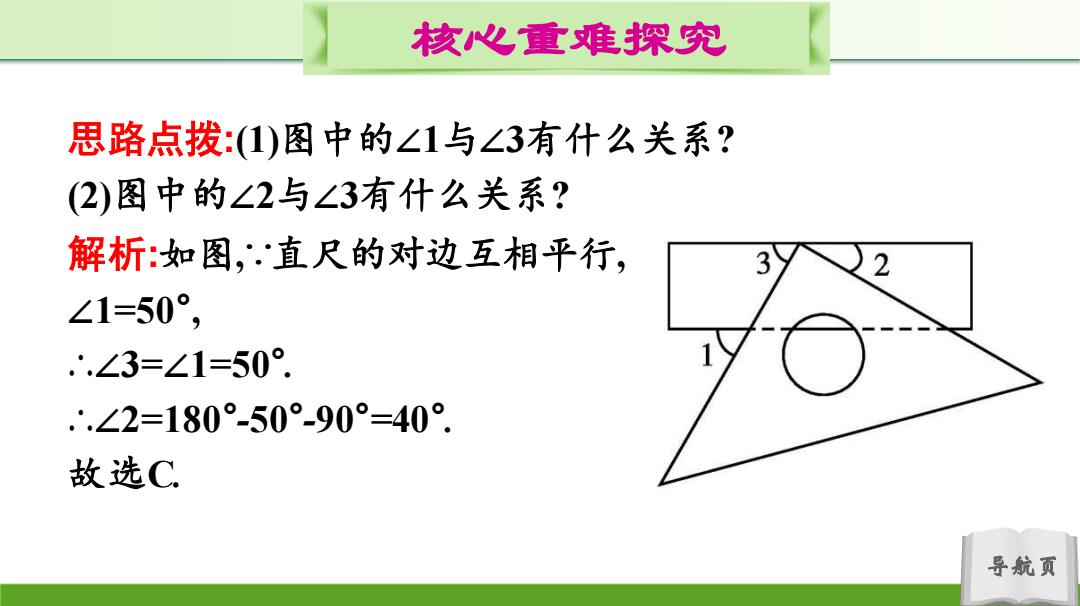
核心重难探究 思路点拨:1)图中的∠1与∠3有什么关系? (2)图中的∠2与∠3有什么关系? 解析:如图,直尺的对边互相平行, ∠1=50°, ..∠3=∠1=50°. ∴.∠2=180°-50°-90°=40°. 故选C 导航页
导航页 核心重难探究 思路点拨:(1)图中的∠1与∠3有什么关系? (2)图中的∠2与∠3有什么关系? 解析:如图,∵直尺的对边互相平行, ∠1=50° , ∴∠3=∠1=50° . ∴∠2=180°-50°-90° =40° . 故选C

核心重难探究 【方法归纳】 解决这类求角的度数的问题,利用直角三角尺的特征及平行 线的性质是常用的方法 导航页
导航页 核心重难探究 【方法归纳】 解决这类求角的度数的问题,利用直角三角尺的特征及平行 线的性质是常用的方法

核心重难探究 知识点二两直线平行,内错角相等 【例2】在同一平面内,将一个直角三角尺按如图所示摆放 在一组平行线上.若∠1=50°,则∠2的度数是( A.50° B.45° C.40° D.35° 导航页
导航页 核心重难探究 知识点二 两直线平行,内错角相等 【例2】在同一平面内,将一个直角三角尺按如图所示摆放 在一组平行线上.若∠1=50° ,则∠2的度数是( ). A.50° B.45° C.40° D.35° C

核心心重难探究 思路点拨:先根据已知条件进行推理,求出部分角的度数,再 根据结论所需条件找出已知角与未知角之间的关系,最后求 解,写出步骤即可. 解析:如图,.alb,∠1=50°, .∴.∠1=∠3=50° b .∴.∠4=90°-∠3=40° .b川c,∴.∠2=∠4=40°.故选C 【方法归纳】 如果已知中涉及直角三角尺,请勿忽略“直角”这个隐含条集颜
导航页 核心重难探究 思路点拨:先根据已知条件进行推理,求出部分角的度数,再 根据结论所需条件找出已知角与未知角之间的关系,最后求 解,写出步骤即可. 解析:如图,∵a∥b,∠1=50° , ∴∠1=∠3=50° . ∴∠4=90°-∠3=40° . ∵b∥c,∴∠2=∠4=40° .故选C. 【方法归纳】 如果已知中涉及直角三角尺,请勿忽略“直角”这个隐含条件
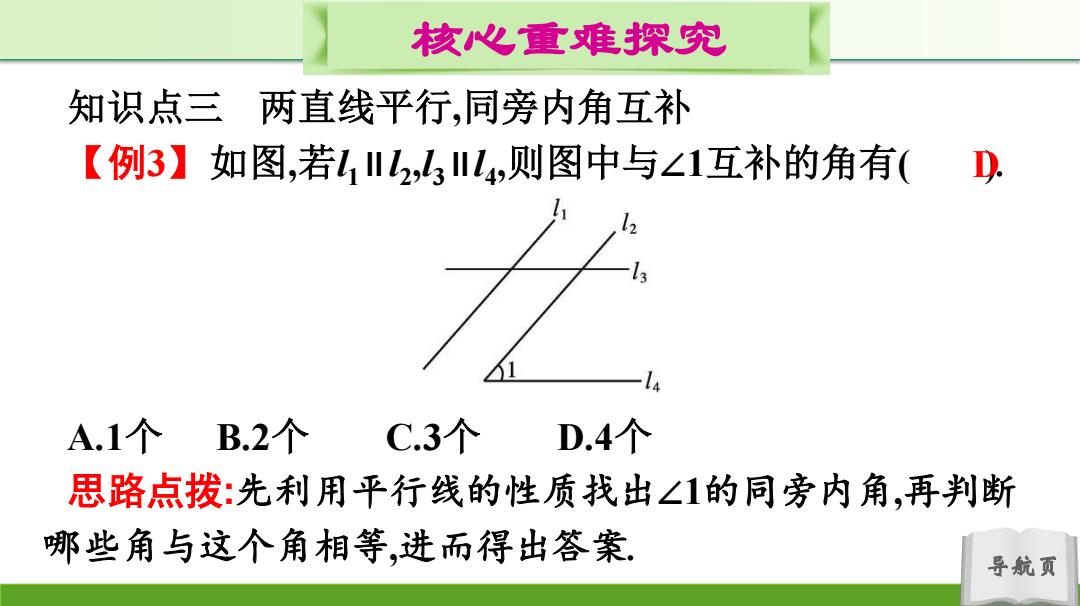
核心重难探究 知识点三两直线平行,同旁内角互补 【例3】如图,若l1I12,Il4,则图中与∠1互补的角有( D. A.1个 B.2个 C.3个 D.4个 思路点拨:先利用平行线的性质找出∠1的同旁内角,再判断 哪些角与这个角相等,进而得出答案 导航页
导航页 核心重难探究 知识点三 两直线平行,同旁内角互补 【例3】如图,若l1∥l2 ,l3∥l4 ,则图中与∠1互补的角有( ). A.1个 B.2个 C.3个 D.4个 思路点拨:先利用平行线的性质找出∠1的同旁内角,再判断 哪些角与这个角相等,进而得出答案. D