
家庭猴四 5.平方差公式 第2课时, 平方差公式的应用
5.平方差公式 第2课时 平方差公式的应用

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升
基础自主梳理 1.如图,从边长为a的大正方形中去掉一个边长为b的小正方 形,然后将剩余部分剪后拼成一个长方形,这个操作过程能验 证的乘法公式是a2-b2=(a+b)(-b) a a b a b bi b 2.计算:2017×1983=3999711 导航页
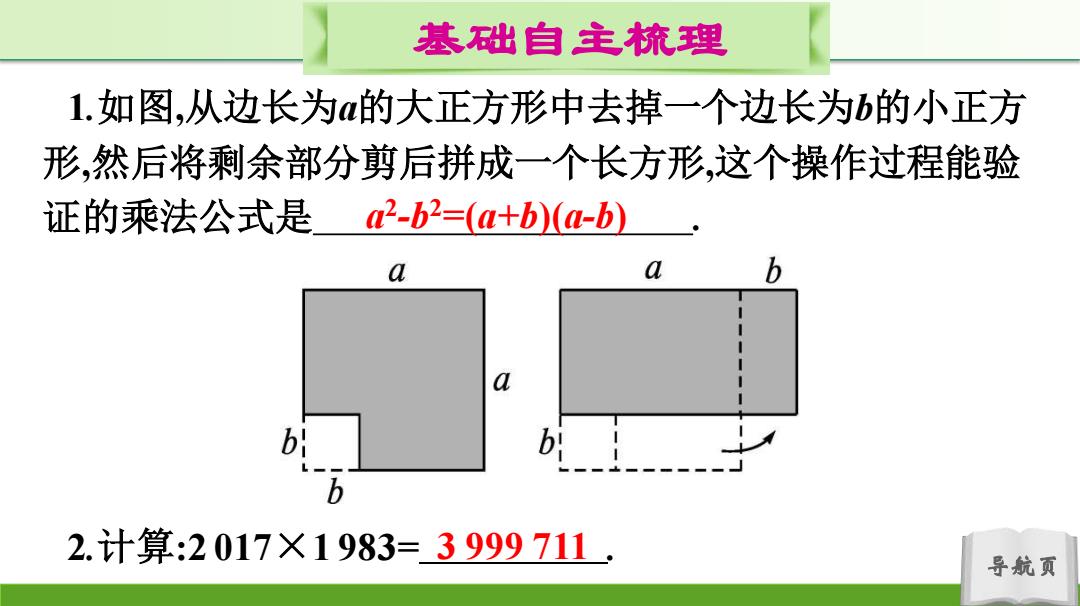
导航页 基础自主梳理 1.如图,从边长为a的大正方形中去掉一个边长为b的小正方 形,然后将剩余部分剪后拼成一个长方形,这个操作过程能验 证的乘法公式是 . 2.计算:2 017×1 983= . a 2 -b 2=(a+b)(a-b) 3 999 711

核心重难探究 知识点一利用平方差公式简便计算 【例1】阅读材料 观察:2009×2007-20082=(2008+1)×(2008-1)-20082=-1. 拓展应用 2007 计算:(1)20072-2008x2006 20072 (2) 008×2006+1 思路点拨:利用平方差公式,将数据2008×2006变形为 (2007+1)X(2007-1),利用平方差公式即可求解. 导航页
导航页 核心重难探究 知识点一 利用平方差公式简便计算 【例1】阅读材料 观察:2 009×2 007-2 0082=(2 008+1)×(2 008-1)-2 0082=-1. 拓展应用 计算:(1) 𝟐 𝟎𝟎𝟕 𝟐 𝟎𝟎𝟕 𝟐-𝟐 𝟎𝟎𝟖×𝟐 𝟎𝟎𝟔 ; (2) 𝟐 𝟎𝟎𝟕 𝟐 𝟐 𝟎𝟎𝟖×𝟐 𝟎𝟎𝟔+𝟏 . 思路点拨:利用平方差公式,将数据2 008×2 006 变形为 (2 007+1)×(2 007-1),利用平方差公式即可求解

核心重难探究 2007 解:(1)20072-2008×2006 2007 20072-(2007+1)×(2007-1) 2007 20072-(20072-1) =2007. 20072 20072 20072 (2 =1. 2008×2006+1(2007+1)×(2007-1)+120072-1+1 导航页
导航页 核心重难探究 解:(1) 𝟐 𝟎𝟎𝟕 𝟐 𝟎𝟎𝟕 𝟐-𝟐 𝟎𝟎𝟖×𝟐 𝟎𝟎𝟔 = 𝟐 𝟎𝟎𝟕 𝟐 𝟎𝟎𝟕 𝟐-(𝟐 𝟎𝟎𝟕+𝟏)×(𝟐 𝟎𝟎𝟕-𝟏) = 𝟐 𝟎𝟎𝟕 𝟐 𝟎𝟎𝟕 𝟐-(𝟐 𝟎𝟎𝟕 𝟐-𝟏) =2 007. (2) 𝟐 𝟎𝟎𝟕 𝟐 𝟐 𝟎𝟎𝟖×𝟐 𝟎𝟎𝟔+𝟏 = 𝟐 𝟎𝟎𝟕 𝟐 (𝟐 𝟎𝟎𝟕+𝟏)×(𝟐 𝟎𝟎𝟕-𝟏)+𝟏 = 𝟐 𝟎𝟎𝟕 𝟐 𝟐 𝟎𝟎𝟕 𝟐-𝟏+𝟏 =1

核心重难探究 【方法归纳】 解决这类问题的关键是熟记平方差公式的结构特征,并将所 求代数式整理成能使用平方差公式的形式,灵活运用平方差 公式求解即可. 导航页
导航页 核心重难探究 【方法归纳】 解决这类问题的关键是熟记平方差公式的结构特征,并将所 求代数式整理成能使用平方差公式的形式,灵活运用平方差 公式求解即可

核心重难探究 知识点二利用平方差公式解决实际问题 【例2】如图,有一个人把一块边长为am 的正方形土地租给马老汉过了一年,他对马 老汉说:“我把你这块地的一边减少5m,另一 边增加5m,继续租给你,你也没吃亏,你看如 何?马老汉一听,觉得好像没吃亏,就答应了.同学们,你们觉得 马老汉有没有吃亏?请说明理由. 思路点拨:()怎么表示马老汉后面所租土地的长和宽? (2)怎么比较面积的大小? 导航页
导航页 核心重难探究 知识点二 利用平方差公式解决实际问题 【例2】如图,有一个人把一块边长为a m 的正方形土地租给马老汉.过了一年,他对马 老汉说:“我把你这块地的一边减少5 m,另一 边增加5 m,继续租给你,你也没吃亏,你看如 何?”马老汉一听,觉得好像没吃亏,就答应了.同学们,你们觉得 马老汉有没有吃亏?请说明理由. 思路点拨:(1)怎么表示马老汉后面所租土地的长和宽? (2)怎么比较面积的大小?

核心重难探究 解:马老汉吃亏了理由如下: .a2-(a+5)(-5)=2-(a2-25) =a2-a2+25=25, .与原来相比,马老汉的土地面积减少了25m2,马老汉吃亏 了. 【方法归纳】 解决这类问题首先要表示出图形中所求部分的面积,再利用 作差法比较大小 导航页
导航页 核心重难探究 解:马老汉吃亏了.理由如下: ∵a 2 -(a+5)(a-5)=a2 -(a 2 -25) =a2 -a 2+25=25, ∴与原来相比,马老汉的土地面积减少了25 m2 ,马老汉吃亏 了. 【方法归纳】 解决这类问题首先要表示出图形中所求部分的面积,再利用 作差法比较大小

新知训练巩固 1.已知=20202,b=2021×2019,则(B) A.a=b B.a>b C.a<b D.a≤b 2.简便计算:2018×2020-20192=-1 导航页
导航页 新知训练巩固 1.已知a=2 0202 ,b=2 021×2 019,则( ). A.a=b B.a>b C.a<b D.a≤b 2.简便计算:2 018×2 020-2 0192= . B -1

新知训练巩固 3.化简:6×(7+1)×(72+1)×(74+1)×(78+1)×(716+1)+1.(结果用 幂的形式表示) 解:原式=(7-1)(7+1)72+1)(74+1)(78+1)716+1)+1 =(72-1)(72+1)74+1)78+1)(716+1)+1 =(741)(74+1)(78+1)(716+1)+1 =(78-1)(78+1)716+1)+1 =(7161)(716+1)+1 =732.1+1 =732 导航页
导航页 新知训练巩固 3.化简:6×(7+1)×(72+1)×(74+1)×(78+1)×(716+1)+1.(结果用 幂的形式表示) 解:原式=(7-1)(7+1)(72+1)(74+1)(78+1)(716+1)+1 =(72 -1)(72+1)(74+1)(78+1)·(7 16+1)+1 =(74 -1)(74+1)(78+1)(716+1)+1 =(78 -1)(78+1)(716+1)+1 =(716 -1)(716+1)+1 =7 32 -1+1 =7 32