
家庭侯亚 2.探索直线平行的条件 第1课时 探索直线平行的条件(1)
2.探索直线平行的条件 第1课时 探索直线平行的条件(1)

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升
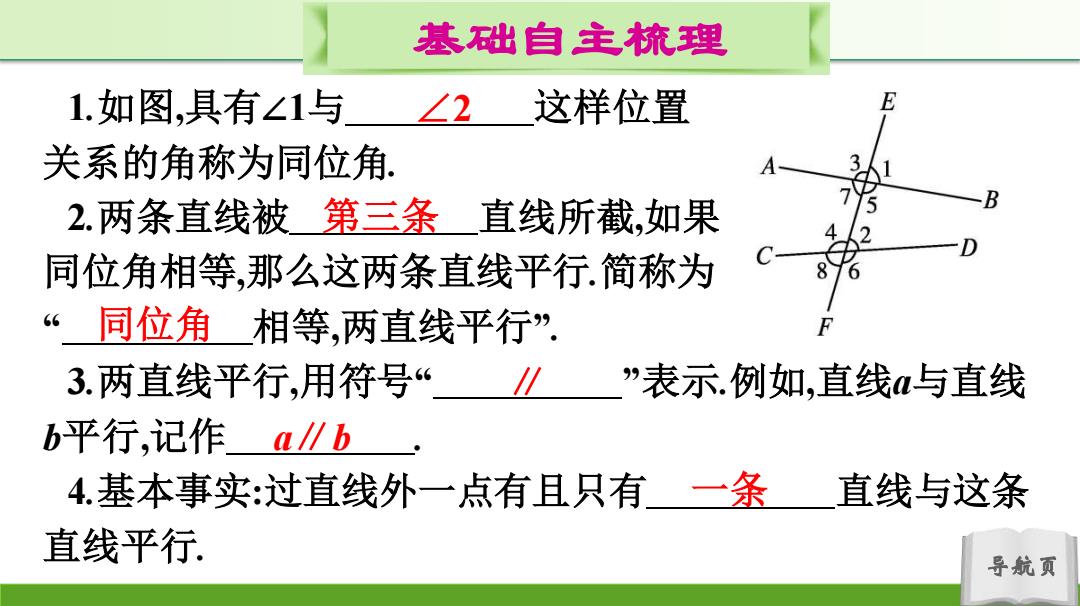
基础自主梳理 1.如图,具有∠1与 ∠2这样位置 关系的角称为同位角 2.两条直线被第三条直线所截,如果 同位角相等,那么这两条直线平行.简称为 “同位角相等,两直线平行” 3.两直线平行,用符号“ ”表示.例如,直线与直线 b平行,记作a∥b 4.基本事实:过直线外一点有且只有一条 直线与这条 直线平行 导航页
导航页 基础自主梳理 1.如图,具有∠1与 这样位置 关系的角称为同位角. 2.两条直线被 直线所截,如果 同位角相等,那么这两条直线平行.简称为 “ 相等,两直线平行” . 3.两直线平行,用符号“ ”表示.例如,直线a与直线 b平行,记作 . 4.基本事实:过直线外一点有且只有 直线与这条 直线平行. ∠2 第三条 同位角 ∥ a∥b 一条

基础自主梳理 温馨提示 关于平行线的基本事实应该注意以下两点: ()必须强调“过直线外一点”.若点在直线上,则经过此点就 没有直线与已知直线平行 (2)“有”表明这样的平行线存在,“只有”说明其“唯一性”. 5.平行于同一条直线的两条直线平行也就是说:如果 bla,cIa,那么b∥c 导航页
导航页 基础自主梳理 温馨提示 关于平行线的基本事实应该注意以下两点: (1)必须强调“过直线外一点” .若点在直线上,则经过此点就 没有直线与已知直线平行. (2)“有”表明这样的平行线存在,“只有”说明其“唯一性” . 5.平行于同一条直线的两条直线 .也就是说:如果 b∥a,c∥a,那么 . 平行 b∥c
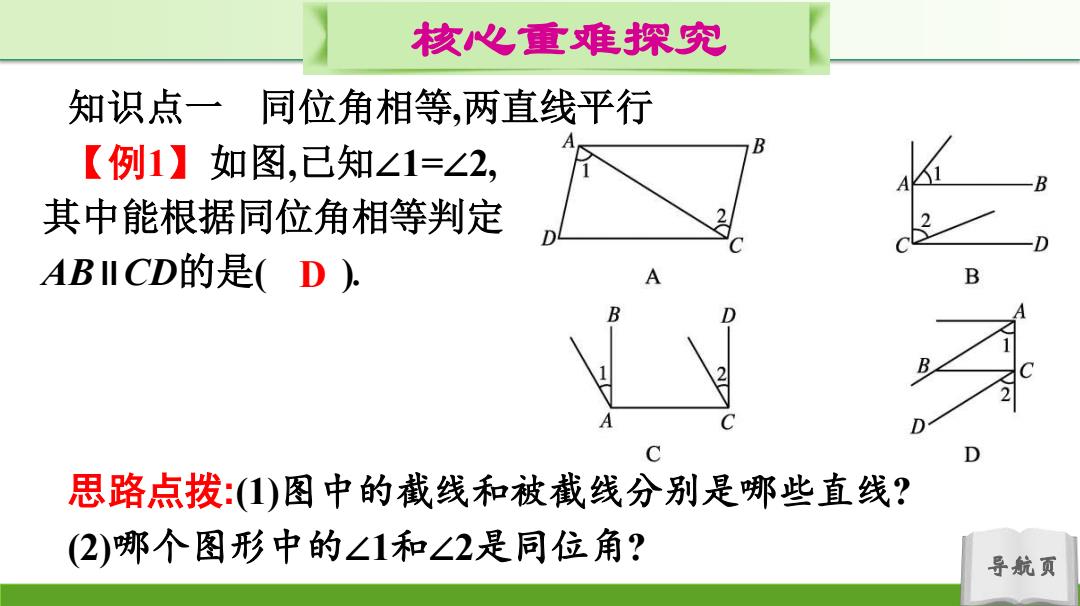
核心重难探究 知识点一同位角相等,两直线平行 【例1】如图,已知∠1=∠2, B 其中能根据同位角相等判定 ABII CD的是(D): 思路点拨:()图中的截线和被截线分别是哪些直线? (2)哪个图形中的∠1和∠2是同位角? 导航页
导航页 核心重难探究 知识点一 同位角相等,两直线平行 【例1】如图,已知∠1=∠2, 其中能根据同位角相等判定 AB∥CD的是( ). 思路点拨:(1)图中的截线和被截线分别是哪些直线? (2)哪个图形中的∠1和∠2是同位角? D

核心重难探究 解析:选项A,B,C中的∠1与∠2均不是同位角;选项D中, .'∠1=∠2, ∴ABCD(同位角相等,两直线平行), 故选D. 【方法归纳】 先确定两个角满足的位置关系,再根据平行线的判定法则来 确定是否平行以及哪两条直线平行 导航页
导航页 核心重难探究 【方法归纳】 先确定两个角满足的位置关系,再根据平行线的判定法则来 确定是否平行以及哪两条直线平行. 解析:选项A,B,C中的∠1与∠2均不是同位角;选项D中, ∵∠1=∠2, ∴AB∥CD(同位角相等,两直线平行). 故选D

核心重难探究 知识点二平行线的基本事实及其推论 【例2】下列说法: ①若a与c相交,则a与b相交; ②若aIb,bIc,则alc; ③过一点有且只有一条直线与已知直线平行; ④在同一平面内,两条直线的位置关系有平行、相交、垂直 三种. 其中错误的有(A). A.3个 B.2个 C.1个 D.0个 导航页
导航页 核心重难探究 知识点二 平行线的基本事实及其推论 【例2】下列说法: ①若a与c相交,则a与b相交; ②若a∥b,b∥c,则a∥c; ③过一点有且只有一条直线与已知直线平行; ④在同一平面内,两条直线的位置关系有平行、相交、垂直 三种. 其中错误的有( ). A.3个 B.2个 C.1个 D.0个 A

核心重难探究 思路点拨:)同一平面内的两条直线有几种位置关系? (2)平行的基本事实是什么? 解析:①若M与c相交,则a与b不一定相交,故错误; ②若aIb,bIc,则alc,故正确; ③过直线外一点有且只有一条直线与已知直线平行,故错误; ④在同一平面内,两条直线的位置关系有平行、相交两种, 故错误 故选A 导航页
导航页 核心重难探究 思路点拨:(1)同一平面内的两条直线有几种位置关系? (2)平行的基本事实是什么? 解析:①若a与c相交,则a与b不一定相交,故错误; ②若a∥b,b∥c,则a∥c,故正确; ③过直线外一点有且只有一条直线与已知直线平行,故错误; ④在同一平面内,两条直线的位置关系有平行、相交两种, 故错误. 故选A

核心重难探究 【方法归纳】 解决这类问题要熟记所学的概念、性质、推论,这些对学好 几何比较关键 导航页
导航页 核心重难探究 【方法归纳】 解决这类问题要熟记所学的概念、性质、推论,这些对学好 几何比较关键

新知训川练巩固 1.如图,∠1=120°,要使aIb,则∠2的大小是( D A.60° B.80° C.100° D.120° 导航页
导航页 新知训练巩固 1.如图,∠1=120° ,要使a∥b,则∠2的大小是( ). A.60° B.80° C.100° D.120° D