
家庭值四 第四章 三角形 2.图形的全等
第四章 三角形 2.图形的全等

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.概念:能够完全重合的两个图形称为全等图形 性质:全等图形的形状和大小都相同 导航页
导航页 基础自主梳理 1.概念:能够完全 的两个图形称为全等图形. 性质:全等图形的 和大小都相同. 重合 形状

基础自主梳理 温馨提示 判断两个图形是不是全等图形,就看两个图形位置发生改变 (如平移、对折等)后是否能完全重合 由全等图形的概念可知: ()全等图形中能够重合的顶点称为对应点;能够重合的线 段称为对应线段;能够重合的角称为对应角,所以全等图形的 对应线段相等、对应角相等、周长相等、面积相等; (2)周长相等的两个图形不一定是全等图形,面积相等的两 个图形也不一定是全等图形: 导航页
导航页 基础自主梳理 温馨提示 判断两个图形是不是全等图形,就看两个图形位置发生改变 (如平移、对折等)后是否能完全重合. 由全等图形的概念可知: (1)全等图形中能够重合的顶点称为对应点;能够重合的线 段称为对应线段;能够重合的角称为对应角,所以全等图形的 对应线段相等、对应角相等、周长相等、面积相等; (2)周长相等的两个图形不一定是全等图形,面积相等的两 个图形也不一定是全等图形
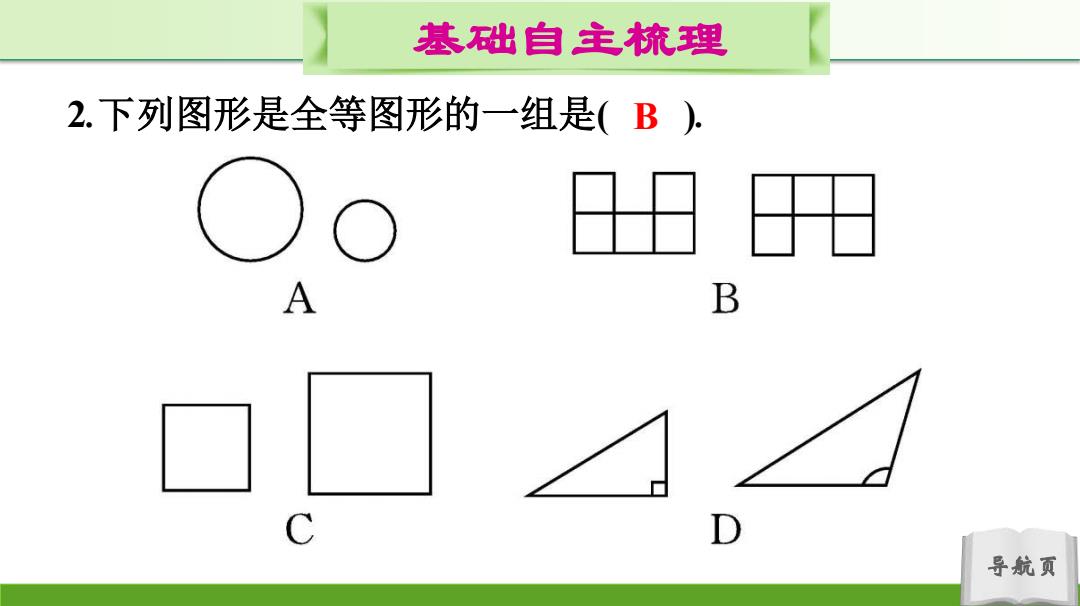
基础自主梳理 2.下列图形是全等图形的一组是(B) A B 导航页
导航页 基础自主梳理 2.下列图形是全等图形的一组是( B )

基础自主梳理 3.全等三角形:能够完全重合 的两个三角形叫做全等 三角形在全等三角形中,能够重合的顶点称为对应顶点,能够 重合的边称为对应边,能够重合的角称为对应角. 全等三角形的对应边相等,对应角相等 导航页
导航页 基础自主梳理 3.全等三角形:能够完全 的两个三角形叫做全等 三角形.在全等三角形中,能够重合的顶点称为对应顶点,能够 重合的边称为 边,能够重合的角称为 角. 全等三角形的对应边 ,对应角 . 重合 对应 对应 相等 相等
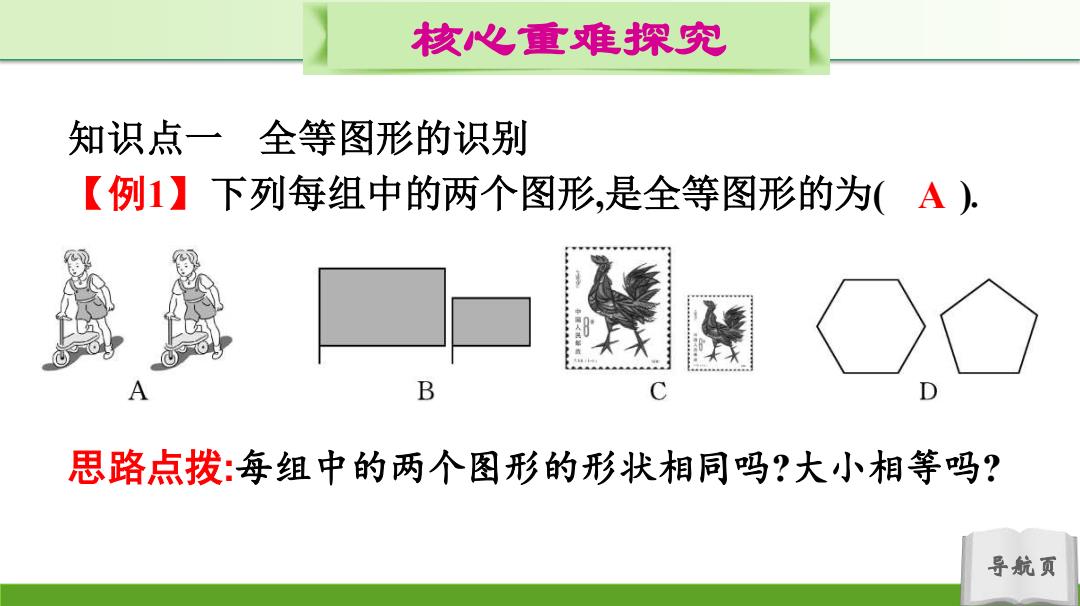
核心重难探究 知识点一全等图形的识别 【例1】下列每组中的两个图形,是全等图形的为(A). B 思路点拨:每组中的两个图形的形状相同吗?大小相等吗? 导航页
导航页 核心重难探究 知识点一 全等图形的识别 【例1】下列每组中的两个图形,是全等图形的为( ). 思路点拨:每组中的两个图形的形状相同吗?大小相等吗? A

核心重难探究 解析:A选项中的两个图形能够重合,为全等图形,正确;B选 项中的两个图形大小不同,不重合,故错误;C选项中的两个图 形大小不一样,不重合,错误;D选项中的图形形状不一样,不重 合,错误 【方法归纳】 判断两个图形是否全等,只要看形状和大小是否完全相同即 可 导航页
导航页 核心重难探究 【方法归纳】 判断两个图形是否全等,只要看形状和大小是否完全相同即 可. 解析:A选项中的两个图形能够重合,为全等图形,正确;B选 项中的两个图形大小不同,不重合,故错误;C选项中的两个图 形大小不一样,不重合,错误;D选项中的图形形状不一样,不重 合,错误
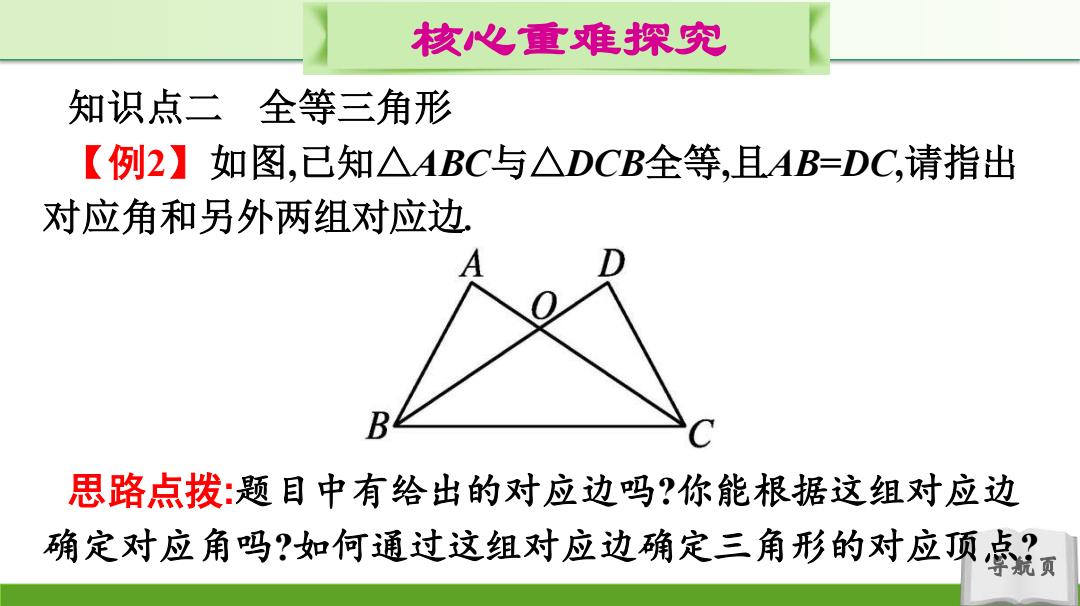
核心重难探究 知识点二全等三角形 【例2】如图,已知△ABC与△DCB全等,且AB=DC,请指出 对应角和另外两组对应边, 思路点拨:题目中有给出的对应边吗?你能根据这组对应边 确定对应角吗?如何通过这组对应边确定三角形的对应顶点? 页
导航页 核心重难探究 知识点二 全等三角形 【例2】如图,已知△ABC与△DCB全等,且AB=DC,请指出 对应角和另外两组对应边. 思路点拨:题目中有给出的对应边吗?你能根据这组对应边 确定对应角吗?如何通过这组对应边确定三角形的对应顶点?

核心重难探究 解:∠A与∠D,∠ABC与∠DCB,∠ACB与∠DBC是对应角, BC与CB,AC与DB是对应边. 【方法归纳】 找全等三角形的对应元素时,抓住其中一组对应元素进行分 析即可得出其他对应元素.如:本题就是抓住题目所给的相等 的边是对应边,再根据公共边是对应边,所有的对应元素就清 晰可见了. 导航页
导航页 核心重难探究 解:∠A与∠D,∠ABC与∠DCB,∠ACB与∠DBC是对应角, BC与CB,AC与DB是对应边. 【方法归纳】 找全等三角形的对应元素时,抓住其中一组对应元素进行分 析即可得出其他对应元素.如:本题就是抓住题目所给的相等 的边是对应边,再根据公共边是对应边,所有的对应元素就清 晰可见了