
家庭值亚 第四章 三角形 4.用尺规作三角形
第四章 三角形 4.用尺规作三角形

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.已知两边及夹角求作三角形的理论依据是三角形全等的 条件边角边(或SAS)” 2.已知两角及其夹边求作三角形的理论依据是三角形全等 的条件“角边角(或ASA)” 3.已知三边求作三角形的理论依据是“边边边(或SSS)” 导航页
导航页 基础自主梳理 1.已知两边及夹角求作三角形的理论依据是三角形全等的 条件“ ” . 2.已知两角及其夹边求作三角形的理论依据是三角形全等 的条件“ ” . 3.已知三边求作三角形的理论依据是“ ” . 边角边(或SAS) 角边角(或ASA) 边边边(或SSS)

核心重难探究 知识点 作三角形 【例题】尺规作图:(画出图形,保留作图痕迹,不写作法) 已知:∠a,线段a,b. 求作:△ABC,使∠B=∠a,AB=b,BC=u. b 思路点拨:要作的图形是三角形,实质是在平面内确定三个 顶点的位置.由于要求∠B=∠α,作一个角即确定了顶点B,只要 在角的两边上再确定其余两个顶点即可 导航页
导航页 核心重难探究 知识点 作三角形 【例题】尺规作图:(画出图形,保留作图痕迹,不写作法) 已知:∠α,线段a,b. 求作:△ABC,使∠B=∠α,AB=b,BC=a. 思路点拨:要作的图形是三角形,实质是在平面内确定三个 顶点的位置.由于要求∠B=∠α,作一个角即确定了顶点B,只要 在角的两边上再确定其余两个顶点即可
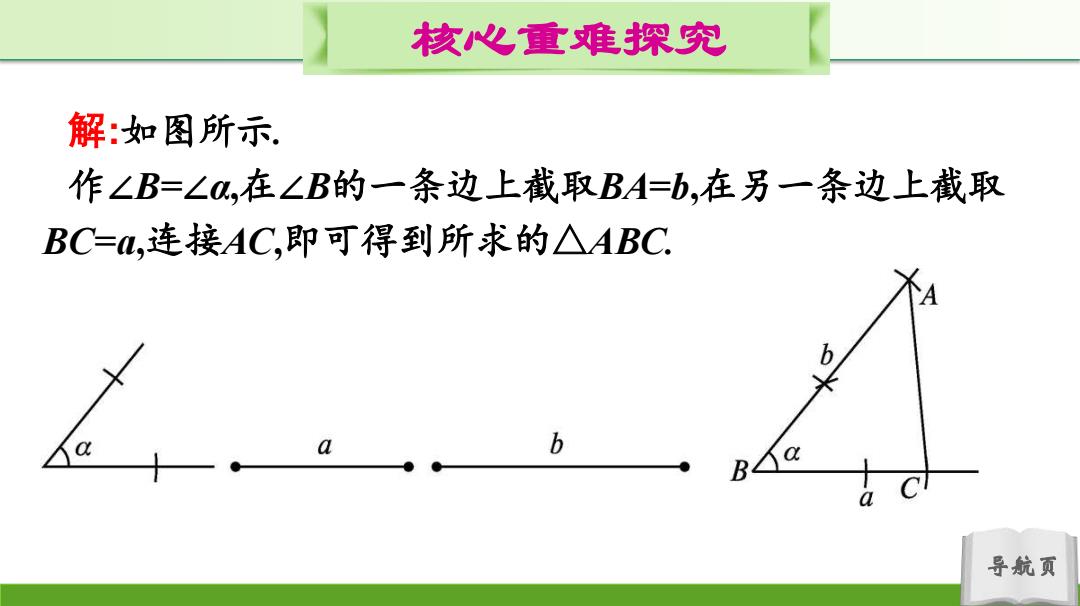
核心重难探究 解:如图所示 作∠B=∠α,在∠B的一条边上截取BA=b,在另一条边上截取 BC=M,连接AC,即可得到所求的△ABC b 导航页
导航页 核心重难探究 解:如图所示. 作∠B=∠α,在∠B的一条边上截取BA=b,在另一条边上截取 BC=a,连接AC,即可得到所求的△ABC

核心重难探究 【方法归纳】 在利用“边角边”作三角形时,一般先作出所给的角,再在角 的两边上分别截取线段,使两边等于所要求的线段 导航页
导航页 核心重难探究 【方法归纳】 在利用“边角边”作三角形时,一般先作出所给的角,再在角 的两边上分别截取线段,使两边等于所要求的线段

新知训练织固 1.根据下列已知条件,能画出唯一的△ABC的是(C) A.AB=3 cm,BC=7 cm,AC=4 cm B.AB=3cm,BC=7cm,∠C=40° C.∠A=30°,AB=3cm,∠B=100° D.∠A=30°,∠B=100°,∠C=50° 导航页
导航页 新知训练巩固 1.根据下列已知条件,能画出唯一的△ABC的是( ). A.AB=3 cm,BC=7 cm,AC=4 cm B.AB=3 cm,BC=7 cm,∠C=40° C.∠A=30° ,AB=3 cm,∠B=100° D.∠A=30° ,∠B=100° ,∠C=50° C

新知训练织固 2.已知线段a,作等边三角形ABC,使AB=M,作法如下:①作射线 AM;②连接AC,BC;③分别以点A和点B为圆心,以的长为半 径作圆弧,两弧交于点C,④在射线AM上截取AB,使AB=,其合 理的顺序为(C), A.①②③④ B.①④②③ C.①④③② D.②①④③ 导航页
导航页 新知训练巩固 2.已知线段a,作等边三角形ABC,使AB=a,作法如下:①作射线 AM;②连接AC,BC;③分别以点A和点B为圆心,以a的长为半 径作圆弧,两弧交于点C;④在射线AM上截取AB,使AB=a.其合 理的顺序为( ). A.①②③④ B.①④②③ C.①④③② D.②①④③ C

新知训练巩固 3.根据下面所给的条件作△ABC,使∠A=∠a,∠B=∠阝,AB=C.(只 保留作图痕迹,不要求写出作法) a 导航页
导航页 新知训练巩固 3.根据下面所给的条件作△ABC,使∠A=∠α,∠B=∠β,AB=c. (只 保留作图痕迹,不要求写出作法)

新知训练织固 解:如图所示 △ABC即为所求作的三角形. \c 导航页
导航页 新知训练巩固 解:如图所示. △ABC即为所求作的三角形