
目录 第一章 有理数 1.1 正数和负数 ……**………*………*……*………………*…1 1.2 有理数 3 第1课时 有理数……………………………………………3 第2课时数轴…6 第3课时相反数…9 第4课时绝对值 11 1.3有理数的加减法…13 第1课时有理数的加法(一)… 13 第2课时有理数的加法(二)………16 第3深时有理数的减法… 19 1.4有理数的乘除法…22 第1深时有理数的乘法(一)…22 第2课时有理数的乘法(二)……… 25 第3课时有理数的除法………………28 1.5有理数的乘方…31 第1课时乘方(一)………31 第2课时乘方(二)… 33 第3深时科学记数法…… 36 第4课时近似数…… 38 章末小结… 41 第一章检测… 44 第二章整式的加减 2.1整式……48 第1课时整式(一)…… 48 第2课时整式(二)… 51 2.2整式的加减…53 第1深时整式的加减(一)…… 53 第2课时整式的加减(二)…55 章末小结… 59 第二章检测… …………62 1

目录 第三章一元一次方程 3.】从算式到方程…65 第1课时一元一次方程…65 第2深时等式的性质… 67 3.2解一元一次方程(一)—合并同类项与移项…70 第1课时解一元一次方程(一)—合并同类项与移项(一)…70 第2课时解一元一次方程(一)—一合并同类项与移项(二)…72 3.3解一元一次方程(二)一去括号与去分母…75 第1课时解一元一次方程(二)—去括号与去分母(一)…75 第2课时解一元一次方程(二)—去括号与去分母(二)…78 3.4实际问题与一元一次方程…81 第1课时实际问题与一元一次方程(一)…81 第2课时实际问题与一元一次方程(二)…84 章末小结… 88 第三章检测…92 第四章几何图形初步 4】几何图形…96 第1课时立体图形与平面图形(一)…… 96 第2课时立体图形与平面图形(二)…98 第3课时点、线、面、体… 101 4.2直线、射线、线段… 103 第1深时直线、射线、线段(一)… 103 第2课时直线、射线、线段(二)………… 106 4.3角……………………………… 109 第1课时角…109 第2课时角的比较与运算… 111 第3课时余角和补角… 114 4.4课题学习设计制作长方体形状的包装纸盒 118 章末小结…122 第四章检测… 125 期末检测…129 2

第一章 有理数 1.1 正数和负数 【学习目标】 1.了解负数是从实际需要中产生的,会判断一个数是正数还是负数.(重点) 2.会用正数、负数表示生活中常用的具有相反意义的量.(重点) 3.体会学习负数的必要性,能准确地举出具有相反意义的量的典型实例.(难点) 基础:导学透思 1.在正数前加上符号“一”(负)的 3.在同一个问题中,分别用正数与负 数叫做负数 数表示的量具有相反的意义. 2.0既不是正数,也不是负数 核心·思维激活 激活①正数和负数 A.-18% B.-8% 1.一般情况下,正数前面的“十”号 C.+2% D.+8% 可以省略不写,而负数前面的“一”号必须 解析:用正数和负数可以表示一对具有 存在.这是正数与负数的主要区别之一 相反意义的量.在本题中“增加”和“减 2.对0的理解:0可以表示“没有”, 少”就是一对具有相反意义的量,既然“增 但引入了负数以后,0的意义扩充了,0不 加”用正数表示,那么“减少”就用负数来 仅表示“没有”,还是一个具体确定的数 表示 它是正数与负数的分界. 答案:B 3.在同一个问题中,分别用正数与负 0变式练习 数表示的量具有相反的意义,这也是重要的 1.向东行-50m表示的意义是(B). 考点之一, A.向东行50m 【例1】如果十10%表示“增加10%”, B.向西行50m 那么“减少8%”可以记作(). C.原地不动 D.无法确定 1

家庭作业·数学·七年级·上册·配人教版 激活2正数、负数的应用 方便面的实际重量与70g的差距最多为 在实际生活中,用正数、负数还可以表 5g,即净重范围是65g~75g. 示误差和范围等.如:图纸上标注零件的直 0变式练习 径为Φ50±胎(单位:mm),说明该零件的最 2.观察下面一组数据,探究其规律: 大直径为(50+0.02)mm,最小直径为(50 0.03)mm,直径在这个范围内的零件都是 合格的;某种药品说明书上标明保存温度为 (1)请直接写出第7项与第2020项。 (20士1)℃,表示该药品在(20-1)℃~ (2)如果这一组数据无限排列下去,那 (20+1)℃的范围内保存才合适. 么与哪两个数越来越接近? 【例2】某方便面包装袋上标明净重是 答案:()- 72020 8’202 “(70士5)g”,请问这是什么含义?该种方 (2)-1和1. 便面净重在什么范围内是合格的? 解:含义为方便面的标准净重为70g, 素能·达标训练 。基础巩固 A.1个 B.2个 C.3个 D.4个 1.下列数:-3,0,+5,-32,+3.1 解析:①0不带“一”号,但是它不是正 2,2019,+2018.其中是负数的有 数;③0既不是正数也不是负数;④0℃ 表示有温度,温度为0℃,温度可以为 (B). 负数(零下),也可以为正数(零上) A.2个 B.3个 4.文具店、书店和玩具店依次位于一条东 C.4个 D.5个 西走向的马路上,文具店在书店西边 2.下列不具有相反意义的量是(C). 20m处,玩具店在书店东边100m处, A.前进5m和后退5m 小明从书店沿马路向东走了40m,接着 B.节约3t和浪费10t 又向东走了一60m,此时小明的位置在 C.身高增加2cm和体重减少2kg (A). D.超过5g和不足2g A.文具店 3.下列语句:①不带“一”号的数都是正 B.玩具店 数;②如果a是正数,那么一a一定是负 C.文具店西边40m处 数;③不存在既不是正数,又不是负数 D.玩具店西边60m处 的数;④0℃表示没有温度.其中错误的 5.如果把公元2028年记作+2028年,那么 有(C). 一208年表示公元前208年 2

第一章有理数 6.在图纸上标明某种零件的加工尺寸为 结果(单位:m)分别为+2.1,0, (25士0.003)mm,甲工人加工出来的零 一1.2,一3,一2,十1.这6次记录的实 件尺寸为25.002mm,乙工人加工出来 际水位最高为30.1m,最低为25m. 的零件尺寸为24.995mm,甲工人加工 8.请按照规律在空格处填上适当的数: 出来的零件合格,加工出来的零件允许的 (1)2,-4,6,-8,10,-12,14 最小尺寸是24.997mm. -16. 解析:根据正数和负数的意义可知,图纸 (2)-12,-8,-4,0,4,8,12. 上的(25士0.003)mm,它表示这种零件的 O能力提升 标准尺寸是25mm,误差不超过0.003mm. 9.请任意写出3个小于4的正数,再任意写 加工要求最大尺寸不超过25.003mm, 出3个负数.是否存在既不是正数,也不 最小尺寸不小于24.997mm.所以甲工 是负数的数呢?若有,请写出来:若没 人加工出来的零件合格. 有,请说明理由. 7.某河务局防汛办公室为了能够更好地利用 答案:(答案不唯一)3个小于4的正数: 水资源,对一条河流的水位进行了记录 +3,十2,十0.5:3个负数:-1,-2, 记录的正常水位是28m,另有6次的记录 -4;存在,0. 1.2 有理数 第1课时有理数 【学习目标】 1.理解有理数的意义.(重点) 2.会根据要求把给出的有理数分类.(难点) 3.了解0在有理数分类中的作用.(重点) 基础·导学诱思 1.正整数、0、负整数统称为整 3.所有正整数组成正整数集合,所 数;正分数、负分数统称为分数 有负整数组成负整数集合,所有负数组成 2.整数和分数统称为有理数, 负数集合 3
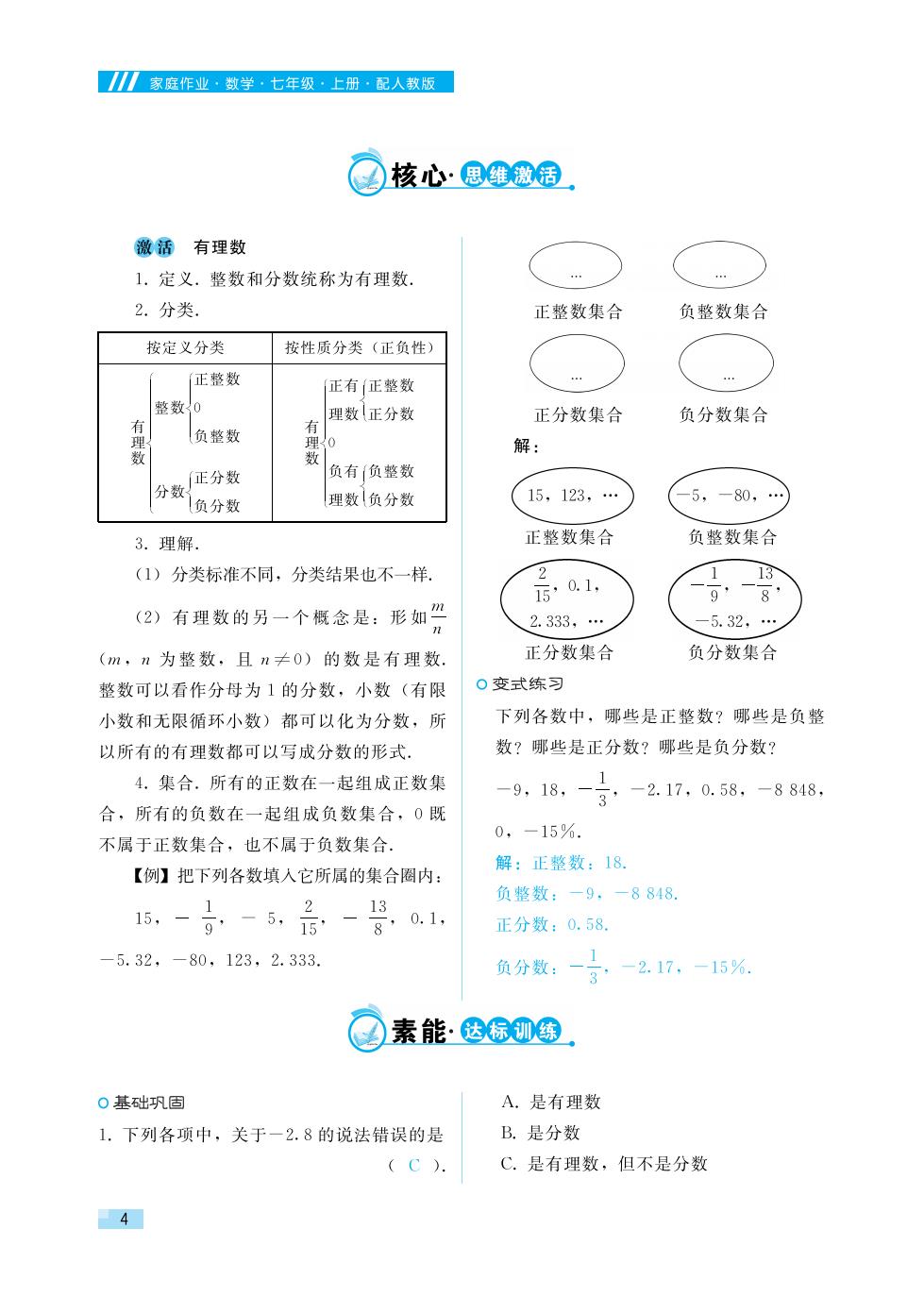
家庭作业·数学·七年级·上册·配人教版 核心·思维激活 激活有理数 1.定义.整数和分数统称为有理数 2.分类. 正整数集合 负整数集合 按定义分类 按性质分类(正负性) 正整数 正有正整数 整数0 理数正分数 交 正分数集合 负分数集合 有 负整数 理 0 数 解: 正分数 负有负整数 分数 理数负分数 15,123,… -5,80, 负分数 3.理解. 正整数集合 负整数集合 (1)分类标准不同,分类结果也不一样. 2 1 13 15’0.1, 9’-8 (2)有理数的另一个概念是:形如” 2.333,… -5.32,… (m,n为整数,且n≠0)的数是有理数. 正分数集合 负分数集合 整数可以看作分母为1的分数,小数(有限 。变式练习 小数和无限循环小数)都可以化为分数,所 下列各数中,哪些是正整数?哪些是负整 以所有的有理数都可以写成分数的形式. 数?哪些是正分数?哪些是负分数? 4.集合.所有的正数在一起组成正数集 -9,18,一3 -2.17,0.58,-8848, 合,所有的负数在一起组成负数集合,0既 0,-15%. 不属于正数集合,也不属于负数集合, 解:正整数:18. 【例】把下列各数填入它所属的集合圈内: 负整数:-9,一8848. 15,- 1 2 13 80.1, 正分数:0.58 -5.32,-80,123,2.333. 负分数:一司 -2.17,-15%. 素能·达标0练 0基础巩固 A.是有理数 1.下列各项中,关于一2.8的说法错误的是 B.是分数 (C. C.是有理数,但不是分数

第一章有理数N D.是非正数 和正数,所以非负数有24,十17,, 2.下列说法正确的是(D). A.所有的正数都是整数 0,共4个 B.不是负数的数一定是正数 0能力提升 C.正有理数包括整数和分数 8.把下列各数填入相应的集合中: D.0不是最小的整数 7、-314,52.-20,-37-1 3.下列说法正确的是(D). A,在有理数中,0没有意义 2 7,0 B.正有理数和负有理数组成全体有理数 正有理数集合:{7,52,号… 22 C.0.3既不是整数,也不是分数,因此 它不是有理数 D.0既不是正数,也不是负数 负有理数集合:{-814,-20,-3 4.下列说法正确的是(D). -1,…}. A.3.14不是分数 整数集合:{7,-20,一1,0,…}. B.正整数和负整数统称为整数 分数集合: C.正数和负数统称为有理数 122 D.整数和分数统称为有理数 {-3.14,5.2-327,…. 5.有理数中,是整数而不是正数的是负整数 自然数集合:{7,0,… 和0,是负数而不是分数的数称为负 9.图中两个圈分别表示正数集合和整数集 整数 合,请写出一些数,并分别填入两个圈 6.有理数20,0,-3,-1.25,1中,属 及它们的重叠部分(每个部分不少于3 个数).请写出这个重叠部分表示什么数 于负整数的是一3: 的集合 解析:负整数是除了0和正整数之外的 整数,显然只有一3符合题意, 7.已知下列8个数:一3.14,24,十17, 正数集合整数集合 -0.01,0,-12.其中整数有 答案:(答案不唯一)如下图 4个,负分数有3个,非负数有 4个. 0.5,1 37 1,2.3 0.-1,-2.-5, 解析:按照有理数的分类填写,整数包括 正整数,0,负整数,所以整数有24, 正数集合 整数集合 十17,0,一12,共4个;负的小数和负 重叠部分表示的是正整数集合: 的分数都是负分数,所以负分数有一3.14, 10.已知有A,B,C三个数集,其中A -72,一0.01,共3个;非负数包指0 {-2,-3,-8,6,7},B={-3, 5
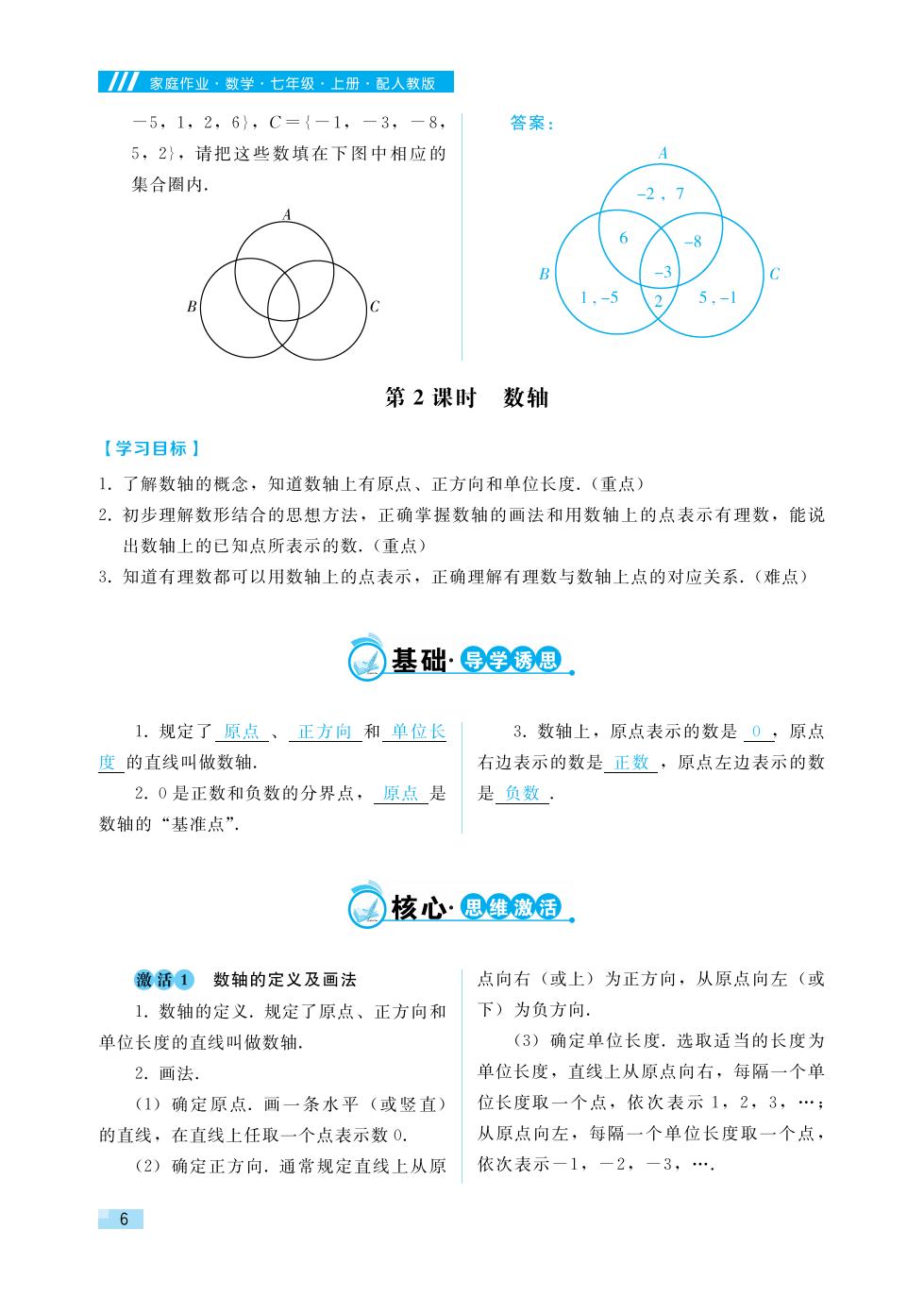
家庭作业·数学·七年级·上册·配人教版 -5,1,2,6},C={-1,-3,-8, 答案: 5,2},请把这些数填在下图中相应的 集合圈内。 -2,7 B 第2课时数轴 【学习目标】 1.了解数轴的概念,知道数轴上有原点、正方向和单位长度.(重点) 2.初步理解数形结合的思想方法,正确掌握数轴的画法和用数轴上的点表示有理数,能说 出数轴上的已知点所表示的数.(重点) 3.知道有理数都可以用数轴上的点表示,正确理解有理数与数轴上点的对应关系.(难点) 基础·导学透思 1.规定了原点、正方向和单位长 3.数轴上,原点表示的数是0,原点 度的直线叫做数轴. 右边表示的数是正数,原点左边表示的数 2.0是正数和负数的分界点,原点是 是负数 数轴的“基准点” 核心:思维激活 激活①数轴的定义及画法 点向右(或上)为正方向,从原点向左(或 1.数轴的定义.规定了原点、正方向和 下)为负方向. 单位长度的直线叫做数轴. (3)确定单位长度.选取适当的长度为 2.画法. 单位长度,直线上从原点向右,每隔一个单 (1)确定原点.画一条水平(或竖直) 位长度取一个点,依次表示1,2,3,… 的直线,在直线上任取一个点表示数0. 从原点向左,每隔一个单位长度取一个点, (2)确定正方向.通常规定直线上从原 依次表示一1,一2,一3,…, 6

第一章有理数 【例1】下列各图中,表示数轴的是 (2)若设a是一个正数,则数轴上表示 ( 数a的点在原点的右边,与原点的距离是a 2-1012一i012一 个单位长度;表示数一a的点在原点的左 A B 边,与原点的距离是a个单位长度 3-2-112一2-1012 【例2】下列语句:①数轴上的点仅能表 C D 示整数;②数轴是一条直线;③数轴上的一 解析:选项A,缺少正方向,所以不是 个点只能表示一个数;④数轴上找不到既不 数轴;选项B,单位长度不统一,不是数 表示正数,又不表示负数的点:⑤数轴上的 轴;选项C,没有原,点,不是数轴;选项 点所表示的数都是有理数.正确的说法有 D,具有了数轴的三要素,正确. (). 答案:D A.1个 B.2个 0变式练习 C.3个 D.4个 1.一些同学在作业中所画的数轴如图所示, 解析:结合数轴上的,点与有理数的特,点 其中,画图正确的是(C). 可知,①是错误的;④是错误的,数轴上既 3-2-10123=2012 不是正数,也不是负数的点是原点;所有的 ① ② 有理数都可以在数轴上找出对应的,点,但数 -1-2-30123 -20 轴上的,点并不都表示有理数,以后学习的无 ③ ④ 理数也可以用数轴上的,点表示,所以⑤也错 A.①②③④ B.①②③ 误.只有②③是正确的,故选B. C.② D.②③ 答案:B 解析:画数轴图要符合数轴的三要素: 【例3】小玉从某地(记为点A)向东走了 原,点、正方向和单位长度.①单位长度不 100m,然后转身向西走了30m,又转身向东 统一;③负数的顺序错了:④没有正方 走了60m,此时小玉在出发点A的哪个方向? 向,只有②是正确的,故选C 与出发点A相距多远? 激活2用数轴表示数及其应用 解:如下图,小玉行走的路线是A→ 1.数对应点.每一个有理数都可以用数 B→C→D,所以由图可知,小玉在出发点 轴上的点表示出来.整数可以直接在数轴上 A的正东方向,且与出发点A相距130m. 找到对应的整数点;分数则可以先将整数分 A B 成若干份(分母的份数),取其中的分子 D 份数. -20020406080100120140 2.点表示数.数轴上的每一个点都表示 0变式练习 一个数(不仅仅是有理数). 2.如图所示,在数轴上有3个点A,B, 3.理解. C,如何移动A,B,C中的两个点,才 (1)借助于数轴把数直观地排列在一条 能使这3个点表示相同的数?有几种移 直线上,便于归类、比较 动方法? 7

家庭作业·数学·七年级·上册·配人教版 A B 长度;②点A向右移动2个单位长度, 43201234 点C向左移动5个单位长度:③点B向 解:有3种移动方法,①点A向右移动 左移动2个单位长度,点C向左移动7 7个单位长度,点B向右移动5个单位 个单位长度 素能·达标训练 0基础巩固 -4或一2: 1.在数轴上,原点及其左边的点表示的数 解析:此题注意考虑两种情况,可以向 是(C). 左移或向右移.以表示一3的点A为起 A.正数 B.负数 点,向左移1个单位长度,即一4:向右 C.非正数 D.非负数 移1个单位长度,即一2 2.在数轴上点A和点B所表示的数分别为 7.数轴上点M表示2,点N表示-3.5, 一2和1,若要使点A表示的数是点B表 点A表示一1,在点M与点N中距离点 示的数的3倍,则应将点A(B) A较远的是点M· A,向左移动5个单位长度 解析:因为,点M距点A为3个单位长 B.向右移动5个单位长度 度,点N距点A为2.5个单位长度,所 C.向右移动4个单位长度 以距离点A较远的是点M。 D.向左移动4个单位长度 O能力提升 解析:因为,点B表示的数的3倍是1× 8.请写出3个有理数,要求同时满足下列3 3=3,点A原来所表示的数为一2,所以 个条件:①其中2个数属于非正数集合; 应把,点A向右移动5个单位长度. ②其中2个数属于非负数集合;③这3个 3.若数轴上的点A到原点的距离是6,则 数都属于整数集合,则这3个数可以是 点A表示的数为(A). 答案不唯一,如:十1,0,一1· A.6或-6 B.6 9.若向西走5m记作一5m,小明从超市出 C.-6 D.3或-3 发先走了-10m,又走了+18m,再走 解析:在数轴上表示一6或6的点与原点 了一10m,请判断出小明现在在何处. 的距离均为6个单位长度,故选A. 解:走一10m表示向西走10m,走 4.数轴上表示一3的点与表示1的点之间的 +18m表示向东走18m,又走了一10m 有理数有无数个. 表示向西走10m,所以小明现在在超市 5.数轴上到表示一5的点的距离和到表示 向西2m处. 一3的点的距离相等的点所表示的数 10.阿健在写作业时,不慎将墨水滴在了数 是一4. 轴上,请你根据图中数值,确定墨水盖 6.如果数轴上点A表示一3,那么与点A 住的整数共有多少个. 相距1个单位长度的点B所对应的数是 8